正因为“太小的结构我们看不清,太大的结构我们看不全”,所以我们需要使用重整化群的方法,不断把系统的重要特征突出,把不重要的特征抹除,最终我们会发现,或许整个世界是由一个个有限的岛屿组成,每个系统都会属于一个岛屿,再无其他。本文从伊辛模型的重整化开始介绍了重整化群理论,然后系统梳理了重整化群和机器学习结合之处的系列研究,最后探讨了与重整化群殊途同归的多尺度动力学建模在探索非平衡动力系统方面的前沿进展,包括因果涌现理论、本征微观态理论、强化学习世界模型等。
撰文 | 陶如意
重整化群在物理领域,尤其是粒子物理和统计物理领域具有非常重要的地位。引用加州大学圣迭戈分校尤亦庄老师(E大)关于重整化群的使用场景的总结就是:太小的结构我们看不清,太大的结构我们看不全。所以,我们需要重整化群来对系统进行截断或者进行“粗糙化”的描述。
关于什么是重整化群,本文主要以我的学习路径为锚点分享对于重整化群的理解。在当前阶段其实就是这样一句话:它本质上是描述系统参数空间动力学的一套图像。最后,我们会再回到E大的描述进行呼应。所以,让我们从动力学的话题开始。
01
什么是重整化群
首先我们先形式化地表示一个系统。对于一个动力系统,我们可以利用这样一个方程来描述:
dx/dt = f(x, θ) (1)
其中x是系统的变量,而θ和f的形式在特定问题下通常是固定的。比如一个弹簧振子的微分方程是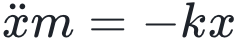 。当然,这里写成了动力学形式,是因为动态系统对我们研究复杂系统的人来说更为常见。而如果我们要建模的系统是一个平衡系统,那么就可以用一个概率分布p(x, θ)来描述这个系统。而下述内容为了方便论述,我们都以复杂系统更常见的动力学系统展示为主,这并不妨碍我们对整个理论的理解。总之呢,我们现在可以用形式化的数学把一个系统描述出来。
。当然,这里写成了动力学形式,是因为动态系统对我们研究复杂系统的人来说更为常见。而如果我们要建模的系统是一个平衡系统,那么就可以用一个概率分布p(x, θ)来描述这个系统。而下述内容为了方便论述,我们都以复杂系统更常见的动力学系统展示为主,这并不妨碍我们对整个理论的理解。总之呢,我们现在可以用形式化的数学把一个系统描述出来。
而这个时候我们再引入尺度的概念。引入尺度意味着什么呢?实际上引入尺度的视角,就好像我们在用不同分辨率的眼睛重新看这个系统,比如我们使用的分辨率更低了,那么我们看到的系统就会更“糊”,丢失了很多细节,但我们还是能看到系统在运动。在这个新的尺度上我们也可以用一套新的动力学方程来描述,比如可以写成
dy/dt = f'(y, θ')(平衡态系统则可以写成p'(y, θ') (2)
在这个新的描述形式下,系统的变量可以和原来不一样,参数可以不一样,就连方程的形式也可以不一样(从f变成了f')。其实各个领域的传统方法,就是这么去处理一个系统不同尺度的。我们在处理每一个尺度上的问题可以说是游刃有余,并且也发明了很多非常成熟的工具用来分析各种动力学中的微分方程和偏微分方程。线性动力学就不用说了,非线性动力学也有诸如流(flow)、混沌、吸引子、分形等丰富的分析工具(推荐书籍:Stenven Strogatz 的 Nonlinear dynamics and chaos)。
不过,物理学家就是这么一群奇怪的物种,总是喜欢另辟蹊径做一些奇怪的事情。他们在对系统不断做粗粒化的过程,发明了重整化群的方法。重整化群这个工具要回答的实际上就是这样一个问题:我们在不断对系统做粗粒化的时候,系统会发生什么样的变化,也就是说在追问的是:系统在不同尺度之间存在什么样的关系?
实际上,延续上文的语言,重整化群要建模的,是不同尺度系统参数的动力学。即
dθ/dl = g(θ, γ) (3)
上面的公式有几个关键点,首先自变量由原来的时间t变成了尺度l,其次因变量是θ,也就是原系统的参数。这是在说,方程建模的是系统的参数随尺度的变化。当然我们能写成上面这条公式的前提,是假设了不同尺度的动力学形式f和f'可以写成基本一致的形式(基本一致这个说法很微妙,我们会在下文给出解释)。这个假设虽然看着很强,但其实在很多物理系统中是非常合理的。
我们以经典的平衡态 Ising model 为例(Ising model 的基本介绍见:伊辛模型 | 集智百科),块粗粒化( block coarse-graining)的操作其实可以近似等价于调控系统的耦合系数(也可以理解成温度,耦合系数和温度有直接的关系)。所以我们会有那张经典的动态 Ising 重整化的图像(如图1所示)。而可以这么做的前提是,不同尺度的 Ising model 它依然是一个 Ising model, 不会变成其他别的比如Potts模型(Potts模型的变量不是二值的)。在这一前提下,公式(3)就描述了一个全新的动力系统,这个系统指的就是原来系统的多尺度视角。我们通过使用动力系统的方法来分析这个系统,也可以得到一系列的系统关于尺度的定量规律。

图1. Ising 模型2维空间的实空间重整化,外场为0。每一列代表的是不同的约化温度。每一行代表的分别是原始系统,1次重整化,2次重整化后的系统。
那么,我们已经得到什么样的规律呢?既然他是一个动力系统,就可以用一个相图来表示,图2分别是 Ising model 1d 和 2d 为例的重整化方程相图。1d情况下没有非平凡的不动点(fixed point),2d时则存在一个非平凡的不动点。而参数空间的不动点意味着在尺度变化的过程中,系统的的参数不发生变化。这其实是一个挺奇怪的现象,意味着粗粒化的过程不会本质改变系统内元素的相互作用基本规则。这只有两种场景才有可能发生:
系统内部元素的关联性要么是0,即没有相互作用;
要么就存在着无穷大的长程关联,所以无论怎么粗粒化我们抹去的只是无关紧要的局部信息。
所以,重整化方程的(非平凡的)不动点在临界系统中其实就对应着相变点。图2中的K是系统的耦合系数,是一个类似于温度的参数,决定了系统的相互作用的强度。并且用这种方法,我们也可以直接计算出系统的临界指数。在有了这样的直观图像之后,感兴趣的同学就可以继续深挖有关于重整化群的数学细节。
资料推荐:
集智百科:Ising模型的重整化 模型的重整化
书籍:Complexity and Criticality、《边缘奇迹:相变与临界现象》
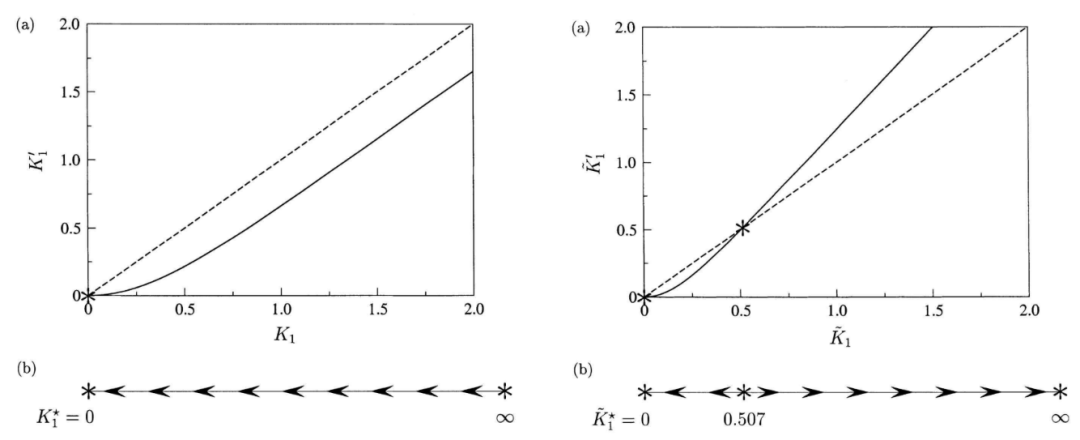
图2. 左图是1维Ising模型的重整化示意图(a)和(b)相图;右图是2维Ising模型的重整化示意图(a)和(b)相图
实际上,还有一个容易被忽略但也很关键的细节,就是在刚刚讨论过程中我们提到重整化群的假设是不同尺度的动力学f和f'基本一致。实际上我们在Ising model的例子中,微观尺度的耦合强度是一阶最近邻相互作用,重整化一次之后会出现更高阶的相互作用,耦合强度K的变化不仅仅是简单数值的变化,其实更精确的表述还涉及到维度的扩展。所以图2右边的相图,其实是更高维动力系统的一个降维。也就是说,这里的耦合强度K其实应该是一个无限维向量,包含了多种类型的相互作用K=(K1, K2, K3,...),其中K1是最近邻相互作用常数,K2是次近邻,K3是三个邻居,以此类推。其能量函数形如:
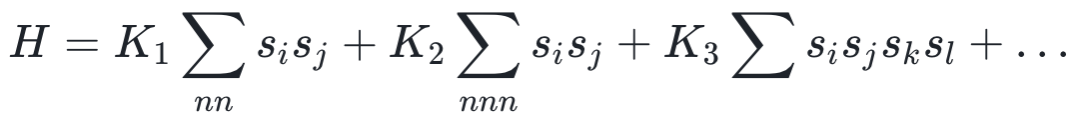
而我们通常讨论的 Ising model 除了K1以外其他系数都为0,所以对原始系统的重整化过程更加精确的描述应该是如图3所示。图3画出了耦合系数的三个维度,每次重整化操作耦合系数在这个空间中变化。
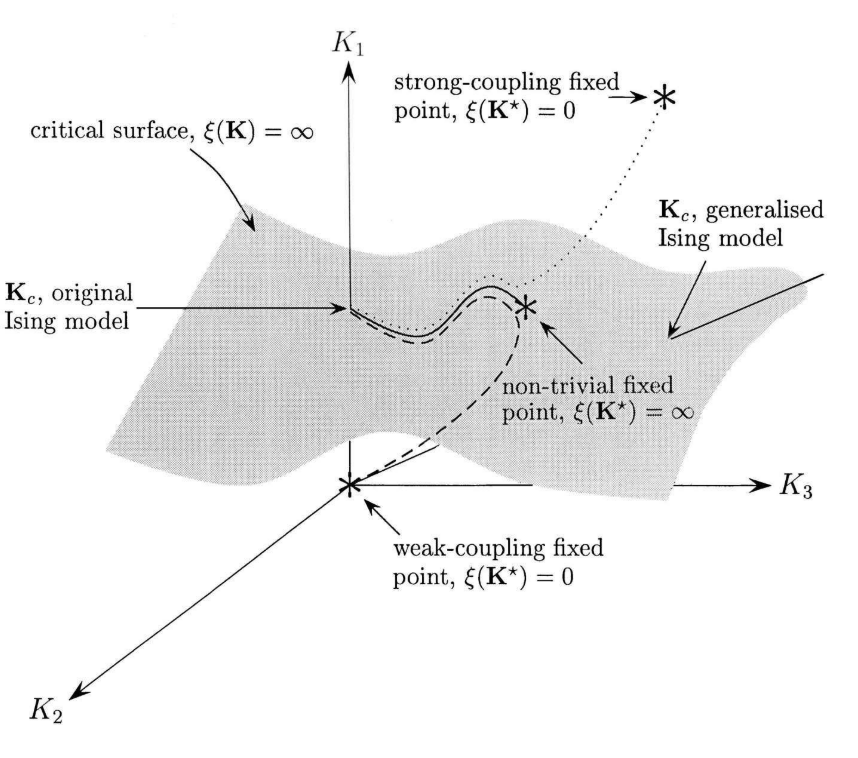
图3. 以3维参数空间示意图。通常我们谈论Ising模型的时候都是指K2和K3两个维度为0。图中标注了三个不动点在三维空间中的位置。图2的一维相图其实是这个空间在K1维度上的投影。图中灰色的面是所有耦合常数都为∞的临界面(Critical surface)
当我们使用重整化群忽略系统的细节之后,还惊喜地发现,自然界中的各类系统虽然千差万别,但只表现出了有限类别的重整化行为。比如铁磁系统的相变和水的气液相变的相变行为居然非常一致。基于这一发现,人们就用不同系统在重整化过程中表现出行为的不同,而对系统进行了分类,这就是普适类(universality class)的概念。普适类的提出使得我们对临界相变系统的理解有了质的飞跃。这就可以回到了开头E大的那句话:正因为“太小的结构我们看不清,太大的结构我们看不全”,所以我们需要使用重整化群的方法,不断把系统的重要特征突出,把不重要的特征抹除,最终我们会发现,整个世界是由一个个有限的岛屿组成,每个系统都会属于一个岛屿,再无其他。
不过,当我们想使用重整化群理论对具体系统进行分析的时候,还是存在一些门槛的,比如我们需要设计合适的重整化策略,而有时候我们其实并不知道应该遵循什么原则来设计这一策略,这非常依赖于科学家的经验甚至是灵感。再比如是不是可以发明一些方法,把整个计算流程自动化,让机器自动去计算普适类,从而解放科学家的生产力,让科学家们去思考更重要的问题。于是,就出现了一批数据驱动和重整化群理论结合的方法。
02
Renormalization Group and Machine Learning
Renormalization Group for Machine Learning
机器学习和重整化群的结合是一个非常前沿但也早就被人关注的领域,从PCA[1]开始就有相关的讨论。并且,深度学习的深度结构和重整化在形式上又有非常多的相似之处:重整化群通过不断粗粒化的方式提取系统的关键特征,而深度学习的每一层也是提取特征的过程,并且不同层的特征也有尺度的含义,越是浅层的神经网络编码的是小尺度的特征,越是深层则编码的就是大尺度的特征。
文章[2]首次明确指出了这种联系,并且尝试构造一个基于受限玻尔兹曼机(Restricted Boltzmann Machine,下文简称 RBM) 的神经网络架构,建立了 Ising 模型 Kadanoff 的块粗粒化和神经网络在解析上的精确映射,证明了深度学习算法可能确实是在用类似于重整化流的模式从数据中提取特征。这对于理解深度学习的运作机制有很大的启发。
[1] Bradde, Serena, and William Bialek. "Pca meets rg." Journal of statistical physics 167 (2017): 462-475.
[2] Mehta, Pankaj, and David J. Schwab. An exact mapping between the variational renormalization group and deep learning. arXiv preprint arXiv:1410.3831 (2014).
[3]是对上篇文章直接的推进——尽管中间过了6年。这篇文章同样使用RBM结构复现了Ising模型的重整化流,甚至能在数值上找到各种临界指数。这让重整化和机器学习的对应更为明确,也更贴近具体的应用。
[3] Koch, Ellen De Mello, Robert De Mello Koch, and Ling Cheng. Is deep learning a renormalization group flow?. IEEE Access 8 (2020): 106487-106505.
与此类探索对应的还有一类文献[4, 5],则直接研究训练好的RBM有什么样的特征,发现了所谓的RBM的重整化群流(RG flow),并且得出结论说RBM的稳定不动点就是一个 non-trivel 的临界点。这个图像和Ising model描述的图像恰好相反(Ising的临界点是不稳定的不动点),背后的原理非常值得进一步探究。
[4] Iso S, Shiba S, Yokoo S. Scale-invariant feature extraction of neural network and renormalization group flow. Phys Rev E. 2018;97(5):1-16. doi:10.1103/PhysRevE.97.053304,
[5] Funai SS, Giataganas D. Thermodynamics and feature extraction by machine learning. Phys Rev Res. 2020;2(3):1-11. doi:10.1103/PhysRevResearch.2.033415
诸如此类的研究都非常有趣,关注的问题核心其实是如何用统计物理的视角更好地理解神经网络的表征。不过这类探索往往局限于某一特定的神经网络框架,通常这个架构就是RBM,因为这个框架几乎就是为了和统计物理对应而设计的。这无论对于解决具体问题,还是对统计物理本身理论的进展而言,在科学层面其实都并没有特别本质的推进。就好像是物理学家们把RBM当做一个玩具一样反复把玩,虽然也有对于临界指数计算的尝试,但受限于RBM的结构,始终没有在更复杂的系统中进一步应用,所以和现实还是有一段距离。
其实除了RBM这一传统的结构之外,CNN,张量网络,甚至各类生成模型都有和RG结合的潜力。我们更需要回答的应该是,这种结合可以有什么样的实际应用,或者对于增强神经网络的能力有什么样的帮助。这就有了下文介绍的另一类的文章,尝试使用RG理论作为神经网络设计的先验知识,真正用于解决实际问题,或者真正能够对物理理论起到实质性的帮助。
Machine Learning for Renormalization Group
这类文章最经典的就是18年发在 Nature Physics 上基于信息论做重整化群的工作[6]。文章的动机是希望使用数据驱动的方式自动构造粗粒化策略,从而对系统实现重整化。而实现这一目标的手段就是约束系统在粗粒化后,宏观变量与原来系统的“环境变量”的互信息最大,而没有其他任何的先验知识。这里的“环境变量”可以理解不参与当前局部的实空间块重整化的其他变量。最终,神经网络学习出的宏观变量就是有关的变量(relevant variable)。这和RG的图像一致,并且用这种方式也能得到临界指数。
[6]Koch-Janusz M, Ringel Z. Mutual information, neural networks and the renormalization group. Nat Phys. 2018;14(6):578-582. doi:10.1038/s41567-018-0081-4
随后发表在PRX上的工作[7]更是从理论层面严格推导了这种基于信息论的粗粒化的解析形式,为重整化策略的构建提供了非常有价值的原则,使得物理学家们有希望摆脱只能依赖于先验知识或者灵感对系统人工设计粗粒化规则的局限 。
[7]. Lenggenhager PM, Gökmen DE, Ringel Z, Huber SD, Koch-Janusz M. Optimal renormalization group transformation from information theory. Phys Rev X. 2020;10(1):1-27. doi:10.1103/PhysRevX.10.011037
更进一步,王磊和尤亦庄老师的工作则是提出最小化全息互信息的原理[8],即每次扔掉的信息之间互信息是最小的,这样同样能保留系统有关的信息,本质上是对前文环境互信息最大化的扩展。并且更fancy的是,他们引入了可逆神经网络(Invertible Neural Network),使得重整化过程扩展成了一个真正的群操作——而不是传统重整化的半群操作。这就使得学习出的神经网络本质上构成了一个生成模型:不仅可以类似传统重整化的方式提取关键变量,还能实现“逆重整化”重新采样出原来尺度的构型。这种建模的好处是,神经网络的每一层表征都可以对应到实际的物理含义。这篇文章的后续更多的是在探讨将这种框架应用于实际的任务时[9],比传统的方法会更具有哪些可解释性。目前还并没有在理论层面进一步展开分析。
[8] Hu HY, Li SH, Wang L, You YZ. Machine learning holographic mapping by neural network renormalization group. Phys Rev Res. 2020;2(2):23369. doi:10.1103/PhysRevResearch.2.023369
[9]Sheshmani A, You Y zhuang, Fu W, Azizi A. Categorical representation learning and RG flow operators for algorithmic classifiers. Mach Learn Sci Technol. 2023;4:20.
另外,尤亦庄老师团队还有一个有趣的工作[10],他们设计了一个自训练的框架,只要给定系统的对称性而不用给出具体的模拟数据,就可以自动发现系统的普适类。基本的思路是构建一个“细粒度”的模型和一个“粗粒度”的模型,让粗粒度模型尽可能生成和细粒度模型相似的构型,这一过程模拟了重整化过程系统的变化,并且再使用第三个模型作为重整化方程学习器,学习上述两个系统参数的动力学关系。三个模型一起运转起来后,就可以建模出对应对称性系统的重整化群方程,以及对应的临界指数。
[10]Hou W, You YZ. Machine Learning Renormalization Group for Statistical Physics. arXiv Prepr. Published online 2023:1-13.
03
非平衡态系统的多尺度建模
不过,由于重整化群理论本身主要还是在平衡系统中有很多出彩的分析,到这里为止我们讨论的也主要都是关于平衡态模型的重整化。这一方面是因为,对于非平衡态系统,问题的复杂程度上升了不止一个水平,其实到目前为止依然没有什么好的分析手法能够得出和平衡态类似的统一理论。而复杂系统更多的研究对象其实是动力学系统,这类系统往往都是处于非平衡态。另外,非平衡态的分析除了缺乏完善的基础理论之外,也没有像 Ising model 这样研究的非常透彻的经典系统作为toy model供科学家们把玩,所以重整化群相关的工作并不像平衡态系统那样丰富,更别提数据驱动相关的重整化建模工作了。
然而,多尺度的动力学建模在另一些领域中却百花齐放。因为人们早就意识到了无论是对于动力系统的预测还是调控,不同尺度的信息确实是会发挥不同的作用:小尺度的高频信息对于短期预测有帮助,而大尺度的低频信息则在长期建模中起到关键作用。从Reduced-Order Model (ROM),到 Equation-free Model (EFM),再到现在前沿的因果涌现理论(Causal Emergence Theory),这些方法都是在用各自的原则尝试对一个动力系统进行降维或者简化。
而利用数据驱动的方法对动力系统进行降维的工作,近年来在学术界也有百花齐放之感。陈晓松老师团队开发的本征微观态方法从数据出发,使用奇异值分解方法对物理系统的数据进行模式分解,并在这些模式中发现了明确的物理含义[11],这套方法不仅可以求解经典平衡系统的临界相变问题,还在许多复杂系统(包括集群系统,湍流,气候,金融,量子等等)中都取得了突破性的进展。
[11] Hu GK, Liu T, Liu MX, Chen W, Chen XS. Condensation of eigen microstate in statistical ensemble and phase transition. Sci China Physics, Mech Astron. 2019;62(9). doi:10.1007/s11433-018-9353-x
而[12,13]等一系列的工作结合了数据驱动的方法和Koopman算子(Koopman算子是一个对非线性动力系统线性化的算子,但很难计算)实现对动力学的模式分解(Dynamic Mode Decomposition)或者隐空间的学习。还有启发于EFM,直接使用机器学习的降维方法(如VAE等),将系统的变量降维后直接在隐空间学习动力学——这被称之为有效动力学(effective dynamics)——从而实现对系统更好的预测[14]。
[12] Khazaei H. A data–driven approximation of the koopman operator: extending dynamic mode decomposition. AIMS. 2016;X(0):1-33.
[13] Lusch B, Kutz JN, Brunton SL. Deep learning for universal linear embeddings of nonlinear dynamics. Nat Commun. 2018;9(1). doi:10.1038/s41467-018-07210-0
[14] Vlachas PR, Arampatzis G, Uhler C, Koumoutsakos P. Multiscale simulations of complex systems by learning their effective dynamics. Nat Mach Intell. 2022;4(4):359-366. doi:10.1038/s42256-022-00464-w
另外,强化学习领域中基于模型学习的 world models 相关的概念,像是从自己的世界观中开辟出了一个新的但是非常类似的想法[15]:尝试将和主体互动的环境用一个低维的模型来表示,从而提高预测和控制任务的效率,也已经成为这个领域非常前沿的话题。

图4. 我们用于预测的信息不是系统的全部,而只需要一个简化的表征
[15] Ha D. World Models. Published online 2018.
总之,由于我们可以获取的数据越来越多,而要处理的系统也越来越复杂,人们也已经发现引入多尺度的视角对动力学建模,无论是提高运算效率,还是获取对于最终任务的关键低维变量都十分重要,这类方法的思想也在逐渐成为解决实际复杂问题的主流。而这些领域的起源乍一看和重整化群毫无关联,却殊途同归,用另一种方式来到了相似的问题上。甚至因为没有很强的理论约束,使得这些方法有时候在使用时看上去十分“简单粗暴”,但却神奇地在各个领域渗透,成为这些领域解决问题的重要思路。这些相关的话题集智俱乐部因果涌现系列读书会,AI+Science读书会中上有大量相关的资料可以供大家学习和参考,即将开始的因果涌现读书第五季会进一步向大家展示更多的前沿工作。
04
总结
本文从动力学的视角出发,尽量用图像的形式介绍了重整化群方法的基本思路,并且在第二部分介绍了机器学习和重整化群结合的前沿工作。这类工作充满了奇思妙想,并且也确实为重整化群理论更广泛和更智能的应用提供了非常好的解决方案。在第三部分,我用非常粗糙的视角罗列了动力学多尺度建模的工作,展示了这一领域的多元和热闹,而这一类问题本质上都是对非平衡动力学系统问题多尺度解决方案的探索,并且确实对解决实际问题提供了非常重要的启发。另外,还有一个本文没有提到,但对于复杂系统多尺度建模来说也非常重要的领域:即复杂网络的重整化。这类研究相对来说更为独立,关注如何用一个更小的网络来表示一个大的复杂网络,以解决大网络上的复杂计算问题,同样也是一个极具潜力的领域。
不过无论是动力学多尺度建模还是复杂网络的重整化,尽管吸引了科学家的驻足,目前还并没有出现像平衡态重整化理论那样的统一理论,帮助我们真正认识复杂系统内在的统一性。但我们依然可以相信,在不久的将来,我们也能发现这些复杂系统的岛屿所处何方。
作者简介
陶如意,北京师范大学系统科学博士在读。研究方向为复杂系统建模,关注多尺度动力学、规模法则、重整化、深度学习等。
本文经授权转载自微信公众号“集智俱乐部”。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 