拓扑学家证明了两项新成果，它们为令人困惑的四维图形研究带来了一些秩序。

撰文 | Jordana Cepelewicz

翻译 | mathematici

拓扑学的核心研究对象是被称为流形的空间。例如，球面就是一个二维流形。拓扑学家非常了解这种二维流形。他们还开发了一些工具，让他们能够理解三维流形和五维或更多维的流形。

牛津大学博士后研究员萨姆·休斯（Sam Hughes）说：“但在四维空间中，一切都变得有点疯狂……工具不再起作用，奇异的行为出现了。”正如麻省理工学院的汤姆·莫罗卡（Tom Mrowka）所解释的那样：“有足够的空间来产生有趣的现象，但空间又不能大到让它们分崩离析。”

20世纪90年代初，莫罗卡和哈佛大学的彼得·克朗海默（Peter Kronheimer）正在研究二维表面如何嵌入四维流形。他们开发了表征这些曲面的新技术，从而得以深入了解四维流形原本难以触及的结构。他们的研究结果表明，一大类曲面的成员都以相对简单的方式切入其父流形，并保持一个基本属性不变。但没有人能证明这一点。

今年2月，休斯与布兰迪斯大学的丹尼尔·鲁伯曼（Daniel Ruberman）一起，构建了一系列反例——“疯狂”的二维曲面，它们以数学家认为不可能的方式剖开母流形。这些反例表明，四维流形比数学家们早几十年认识到的更加丰富多彩。“这真是一篇漂亮的论文，”莫罗卡说。“我一直在看。那里有很多美味的小东西。”‍

列出清单

去年年底，鲁伯曼协助组织了一次会议，会议列出了低维拓扑中最重要的未决问题的新清单。在筹备会议的过程中，他查看了1997年的一份重要未解拓扑问题清单。其中包括克朗海默根据他与莫罗卡的合作提出的一个问题。鲁伯曼说：“这个问题就在里面，我觉得它有点被遗忘了。”现在他认为他可以回答这个问题了。

要理解这个问题，首先要考虑两个关键概念：单连通流形和基本群。

单连通流形是没有任何孔洞通过的空间。在一维中，无限直线是单连通的，但圆不是。在二维中，无限平面和球面是单连通的，但甜甜圈的表面不是。

数学家们通过在流形上放置回路，并考虑它们如何变形，来严格区分这种区别。如果任何环路都可以缩成一个点，那么流形就是单连通的。例如，在平面或球面上，这是可能的——想想拉紧一根绳子。但如果绳子绕着一个圆转，它就无法收缩。同样，在甜甜圈的表面上，环绕或穿过中心孔的线圈无法变形为一个点。甜甜圈本身就会妨碍变形。

数学家通过计算“基本群”来对非单连通的空间进行分类，“基本群”的结构反映了循环如何收缩。单连通的流形有一个只有一个元素的“琐碎”基本群。但有孔洞的流形的基本群则更为复杂。

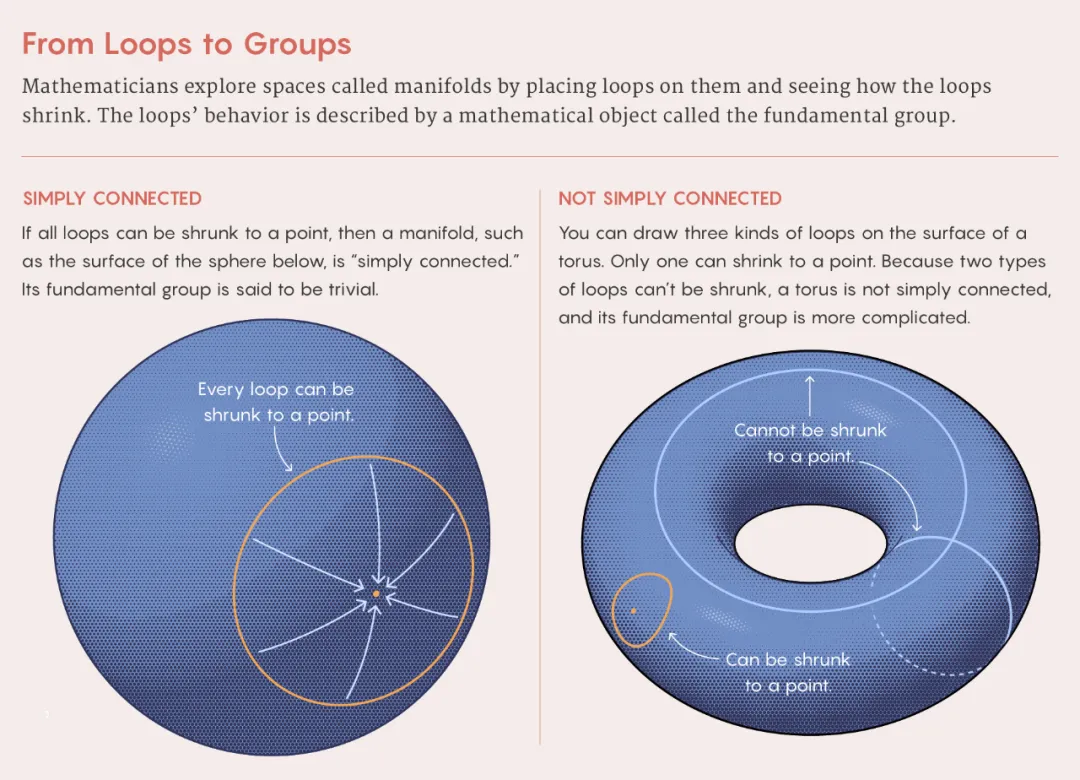
Merrill Sherman/Quanta Magazine

单连通的四维流形仍然非常奇特。为了理解它们，数学家们会思考嵌入其中的二维曲面会发生什么变化。

打个比方，把一圈绳子平铺在一张纸上。你能做的不多。但把它拉高到三维空间，你就可以把它打成复杂的结。你可以用什么方式来操纵绳子——一个一维流形——来阐明它所嵌入的空间的性质。

同样，在更为复杂的四维空间中，二维曲面“在许多不同方面都是整个业务的关键”，鲁伯曼说，“曲面对四维流形的作用远远超出你的想象”。曲面能让你区分流形：如果一个表面可以在一个流形内生存，而不能在另一个流形内生存，那么你就知道这两个流形是不同的。曲面可以用来从旧的流形中建立新的流形。

曲面也有相应的基本群。它们的补集也是如此——即去掉曲面后流形的剩余部分。例如，把球面或甜甜圈表面等二维流形的赤道去掉，就会得到两个断开的半球。但是，如果去掉一个垂直环而不是水平环，甜甜圈的表面仍然是一个整体。同样，根据从四维流形中切割曲面的方法，可以得到不同种类的互补。

Merrill Sherman/Quanta Magazine

早在20世纪90年代，莫罗卡和克朗海默就研究过从四维流形中切除一个二维曲面会发生什么。如果流形本身是单连通的，那么曲面必须满足什么条件才能保证它们的补集也是单连通的呢？

克朗海默和莫罗卡知道，有些曲面的补集可能不是单连通的。但他们的研究似乎表明，另一大类曲面必须始终具有单连通的补集。

近三十年来，没人能在这一类曲面中找到一个补集不是单连通的例子。但在2023年秋天，鲁伯曼遇到了这个问题，他认为自己可以做到。他没有从四维流形入手切出一个曲面，而是从一个具有必要性质的二维曲面入手，围绕它建立了一个流形。

曲面告诉你的关于四维流形的信息远比你所期望的要多得多。

——丹尼尔-鲁伯曼

首先，他将曲面增大为一个四维球体。这个四维球体有一个三维边界，就像球这样的三维物体有一个二维边界一样。鲁伯曼希望在边界的另一侧附加一个精心挑选的四维流形，作为曲面的补充。如果这一招奏效，那么这个流形就会有一个复杂的基本群，而所有物体的基本群加起来又是微不足道的。因此，新构建的四维流形将是单连通的。

但是，为了能够以正确的方式把所有东西粘合在一起，他必须证明新增加的流形的基本群满足各种性质。鲁伯曼说：“我完全不知道该怎么做。”

今年1月，群理论家休斯在布兰迪斯大学发表了一场演讲。鲁伯曼当时就在听众席上。他意识到休斯可能有他正在寻找的缺失部分。两人第二天见了面，几个小时内，他们就想出了所需的主要观点。休斯说，鲁伯曼所缺少的“是群体理论家们已经计算了七八十年的东西”，而“我们一直在做这件事”。一周结束时，他们完成了一个证明。

鲁伯曼说：“我知道一些东西，他也知道一些东西，我们两个人知道的足够多了，就这样完成了。”

由于在证明中使用了群论，“这有点不同寻常，”德克萨斯大学奥斯汀分校的玛吉·米勒（Maggie Miller）说：“它的写法与大多数四维拓扑学家的写法有些不同”。

这一结果再次证明了四维拓扑的复杂性。“表面的有趣嵌入比我们想象的要多得多，”休斯说。这使得流形分类更加困难，也更难证明关于流形的其他结果。

尽管如此，与鲁伯曼一起组织了去年列表会议的马萨诸塞大学阿默斯特分校的伊南奇·贝库尔（İnanç Baykur）还是在3月份宣布了1997年列表中另一个涉及单连通四维流形问题的解决方案。

看来拓扑学家们正在清理门户。

更正：2024年4月23日

本文原版称，如果把一个球体或甜甜圈一分为二，就会得到两个半球（hemispheres）。更准确的说法是两个一半（halves）。

本文经授权转载自微信公众号“数学家”，译自Quanta Magazine。“数学大院”编辑整理。

原文链接

https://www.quantamagazine.org/mathematicians-marvel-at-crazy-cuts-through-four-dimensions-20240422/