群论与博弈论虽然抽象，但也很有故事，历史上众多传奇数学家在这两个领域做出了杰出贡献。人们很早就知道要研究博弈论中的对称性问题需要群论，但用群论研究博弈论仍是冷门方向。
撰文 | 曹志刚、杨晓光等
论文题目：On group structures of strategic-form games
论文地址：https://www.sciencedirect.com/science/article/pii/S2667325822002850?via%3Dihub
问：对于普通读者而言，群论和博弈论都是听起来多少有些神秘色彩的学科领域。事实是这样吗？
答：很多人对于数学都有一种复杂的感情，就是既害怕又喜欢。害怕数学的抽象和困难，喜欢听数学界的八卦和故事。群论和博弈论这两个领域都是非常典型的例子。而这种既爱又怕的复杂矛盾心理很容易让人着迷并产生某种神秘感。如果你对这种抽象的论证没感觉的话，不妨尝试回忆一下暗恋某个人的感觉。所以说数学是我们暗恋的绝佳对象，因为她美丽且高冷，永远得不到从而永远神秘。
群论和博弈论比较抽象比较难就不多说了，为什么有故事呢？因为他们的主要创始人，伽罗华、阿贝尔、冯诺依曼以及纳什等，都不是普通人，都有非凡的故事吸引着我们。所以群论和博弈论都是自带流量的。
问：博弈论和群论这两个自带流量的领域能发生什么有趣的化学反应吗？
答：正如简介中所提到的，早在1944年出版的博弈论的开山之作《博弈论与经济行为》中，冯诺依曼和摩根斯坦就说过，要真正理解清楚博弈论里的对称性问题，多少得用一点群论（“A real understanding of the nature and structure of symmetry is not possible without some familiarity with (at least) the elements of group theory. ——von Neumann, Oskar Morgenstern, 1944.”）。我们尝试用 Midjourney 画了一副伽罗华与冯诺依曼决斗魔方的图片展示这两个领域的交叉（见图1）。
对称性对于博弈论的确很重要，因为对称可以简化问题使得我们把主要精力用于分析核心矛盾。比如博弈建模中经常假设的同质性就是一种简单的对称；表示单种群演化博弈的矩阵博弈也是对称的，因为我们假设种群内的个体都是同质的；对称性也是合作博弈中经常使用的公理。
群论在博弈论中很早就引起了关注。除冯诺依曼和摩根斯坦外，纳什1951年的经典论文也用群论证明了一个比我们熟知的结论更强的结果：有限博弈不仅一定有混合策略纳什均衡，其实还有一个满足原博弈对称结构的“对称均衡”。
对称和群论还可以用来建模焦点均衡。由诺奖得主谢林提出的焦点均衡是博弈论中的一个基础概念。我们知道谢林是罕见的不使用数学研究博弈论的大家。焦点均衡是一个展示其研究风格的绝佳例子。这是一个对多重均衡进行精炼的基本思想，但是其严格定义很难用数学形式化表达。奥地利著名博弈论学家Alós-Ferrer与合作者在2013年发表于 Journal of Economic Theory 的文章尝试用对称性对焦点均衡进行了严格定义：焦点均衡就是所有均衡中最对称的那个。
所以从逻辑上来讲，博弈论和群论理应碰撞出重大的基础性研究成果。但是很遗憾，历史和逻辑并不总是统一的。博弈论和群论的交叉，或者更确切地说用群论来研究博弈论，是一个非常冷门的研究方向，80年来实质性进展屈指可数。
图1 群论遇上博弈论
问：有哪些基本事实可以说明用群论研究博弈论很冷门？
答：目前关于什么叫对称博弈这一基本问题，教科书和学术界都没有完全标准的答案。几乎所有教科书中给出的定义都属于狭义对称博弈。由于策略的名字在狭义对称博弈中起作用，这显然不能令人满意。比如按照此定义，性别大战不属于对称博弈。但是只要把“歌剧”和“足球”两种选择的名字在一个参与人中做一个对调，我们就能发现性别大战也是一种对称博弈。诺奖得主Selten和Maskin等在上世纪八九十年代的研究中用到的对称博弈概念也不能包含性别大战。
问：你们前期在此领域有哪些相关成果？
答：博弈论中很多经典的例子，比如囚徒困境、性别大战，以及硬币匹配博弈，都有一定的对称性。但是按照我们教科书中对对称博弈的定义，只有囚徒困境是对称的，性别大战和硬币匹配博弈都不是。那么如何严格定义进而充分理解这些直观上不同的对称呢？
我们2018年发表于Mathematical Social Sciences 的工作发现可以使用对称群定义三种不同的对称博弈：普通对称博弈，重命名对称博弈以及命名无关对称博弈（图2）。普通对称博弈就是狭义的对称博弈，命名无关对称博弈借助的是纳什曾经使用过的对称群，而重命名对称博弈是我们提出的一类全新的对称博弈。教科书都会讲到的囚徒困境、性别大战和硬币匹配博弈恰好是这三类对称博弈的典型代表。
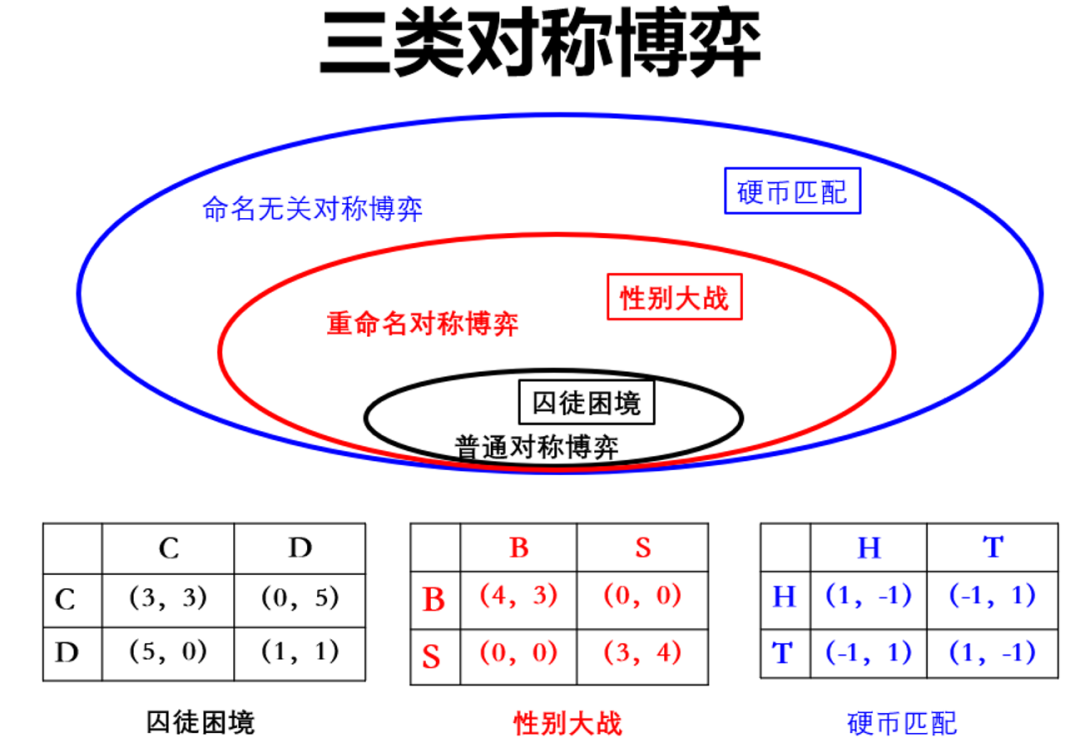
图2 三种不同的对称博弈
问：本文有什么主要贡献？
答：本文是我们前期工作的自然延续。我们前面研究了给定一个博弈，用什么群来刻画不同的对称性。本文研究了如下的逆问题：对于一个置换群，它什么时候有可能成为某个策略博弈的普通对称群，什么时候可以是命名无关的对称群？我们发现Sudholter等在2000年发表于Journal of Mathematical Economics 的论文中提出的“覆盖群”的自然推广恰好是充分必要条件。在此基础上我们进一步研究了策略博弈对称群的更多数学结构。
以上内容节选自期刊Fundamental Research 2024年第3期发表的文章“Z. Cao, G. Li, Z. Tan et al. On group structures of strategic-form games, Fundamental Research 4(3) (2024) 540-549.
主要作者简介
杨晓光 中国科学院数学与系统科学研究院研究员。国家杰出青年科学基金获得者、中国系统工程学会理事长、《系统工程理论与实践》主编。主持国家自然科学基金重大项目等课题，曾获复旦管理学杰出贡献奖等荣誉。
曹志刚 北京交通大学教授。中国“双法”研究会智能决策与博弈分会和中国运筹学会博弈论分会副理事长、中国系统工程学会和中国信息经济学会副秘书长。主持国家自然科学基金优秀青年科学基金等项目。
本文经授权转载自微信公众号“Fundamental Research”，原题目为《Fundamental Research｜杨晓光等：群论遇上博弈论》。
0
推荐
京公网安备 11010502034662号 