埃达·洛夫莱斯,一位19世纪英国贵族女性,英国数学家和作家。她因为结识数学家查尔斯·巴贝奇并看到他发明的差分机而对数学产生兴趣。后来她作为翻译和注释者深入研究了巴贝奇希望制造但未成功的分析机的文章,在注释中给出了计算伯努利数的运算方法——人们认为这是历史上第一段计算机程序,其实现方式与今天的计算机运行几乎相同,包含循环和嵌套循环的思想;她还预见到通用计算的可能。因此她作为第一位程序员而被当代人铭记。

本文经授权节选自《科技群星闪耀时:15个创新创奇》(人民邮电出版社,2024年8月版)第6章《埃达·洛夫莱斯》,有删改,图片为编辑所加。
撰文 | 斯蒂芬·沃尔弗拉姆(Stephen Wolfram)
翻译 | 应俊耀、蔚怡
2015年是埃达·洛夫莱斯(Ada Lovelace)诞辰 200 周年。对于一些人来说,她是计算机史上的伟大英雄;而对于另一些人来说,她只是一个被高估的小人物。很长一段时间以来,我一直对她的真实故事感到好奇。为了准备她的诞辰 200 周年纪念,我决定尝试解开对我来说一直存在的“埃达之谜”。
埃达的早年生活
埃达·拜伦(Ada Byron,她当时的名字)于1815 年 12 月 10 日出生在伦敦,她的父母是上流社会人士。她的父亲拜伦勋爵(George Gordon Byron)当时 27 岁,刚刚因其诗歌而成为英国的知名人物。她的母亲安妮·伊莎贝拉·米尔班克(Anne Isabella Milbanke)23 岁,投身于进步事业,继承了温特沃思(Wentworth)男爵夫人的头衔。埃达的父亲说,他给她取名“埃达”是因为“这个名字简短、古老、有韵味”。

埃达·洛夫莱斯(Ada Lovelace,1815-1852) 丨图片来源:New York Public Library
埃达的父母可以说是截然相反的人。拜伦一生放荡不羁,也许是 19 世纪最具“坏小子”形象的人物,童年时期有过黑暗的经历,后来也有过很多浪漫的和其他过激的行为。除了写诗和无视当时的社会规范,他还经常做一些不寻常的事:他在剑桥大学的宿舍里养了一只温顺的熊;在意大利与诗人和“大台阶上的五只孔雀”一起生活;写了一本亚美尼亚语语法书;假如不是英年早逝的话,他或许还会继续率领军队参加希腊独立战争(雅典至今还矗立着一座纪念他的大雕像),尽管他本人从未受过任何军事训练。
而安娜贝拉·米尔班克(安妮·伊莎贝拉的昵称)则是一位受过教育、虔诚且相当得体的女性,热衷于改革和公益事业,她被拜伦昵称为“平行四边形公主”(Princess of Parallelograms)。她与拜伦的婚姻非常短暂,在埃达只有5 周大的时候就破裂了,埃达自此再也没有见过拜伦(尽管拜伦在自己的书桌上放着她的照片,并在诗歌中极尽赞美地提到过她)。拜伦在 36 岁时去世,正值其名望的巅峰时期,而当时埃达只有 8 岁。围绕他的丑闻足以写成数百本书,拜伦夫人(埃达母亲的自称)的支持者和拜伦的支持者之间的公关战持续了一个世纪甚至更久。
埃达在母亲租来的乡间庄园里度过了孤独的童年,陪伴她的只有家庭女教师和助教,还有她的宠物猫“泡芙夫人”(Mrs. Puff)。埃达的母亲经常因为各种(相当古怪的)健康疗法而不在家,她对埃达实施了一套教育体系,包括长时间的学习和自我控制练习。埃达学习了历史、文学、语言、地理、音乐、化学、缝纫、速记,数学(部分通过经验方法教授)达到了初等几何和代数的水平。埃达11 岁的时候,跟着母亲和随从们一起到欧洲进行了为期一年的旅行。回来后,埃达热衷于研究她所谓的“飞行学”(flyology),并想象如何用蒸汽动力机械模仿鸟类飞行。
但后来她得了麻疹(也可能是脑炎),最后卧床不起,身体欠佳长达三年之久。她最终在 17 岁时及时恢复了健康,遵循当时社交名媛的习俗,去伦敦参加了一个社交季。1833 年 6 月 5 日,在她“进宫朝见”(即觐见国王)26 天后,她参加了 41 岁的英国数学家查尔斯·巴贝奇(Charles Babbage,其长子与埃达同龄)的家庭聚会。显然,她给主人留下了深刻的印象,主人再次邀请她及其母亲,观看他新造的差分机的演示。这是一个 2 英尺高的手摇装置,由 2000 个黄铜零件组成,现在陈列在伦敦的科学博物馆。

图片来源:Science Museum, London INV-1862-89
埃达的母亲称它为“思考机器”(thinking machine),并报告说它“取了几个数的 2 次和 3 次幂,并解出了一个二次方程的根”。这台机器改变了埃达的人生轨迹。
查尔斯 · 巴贝奇
查尔斯·巴贝奇有怎样的故事呢?他的父亲是一位积极进取、事业有成的金匠和银行家(尽管与他本人关系疏远)。经过多所学校和导师的推荐,巴贝奇前往剑桥大学学习数学,但没过多久他就决心改革那里的数学教学方式,并与他的毕生好友约翰·赫歇尔(John Herschel,天王星发现者之子)和乔治·皮科克(George Peacock,后来成为抽象代数的先驱)一起成立了分析协会(后来成为剑桥哲学学会),推动改革,比如用莱布尼茨基于函数的(“欧陆式”)微积分符号取代牛顿基于点的(“英国式”)微积分符号。

查尔斯 · 巴贝奇丨图片来源:wikimedia
1814 年(埃达·洛夫莱斯出生的前一年),巴贝奇从剑桥大学毕业,与新婚妻子搬到伦敦居住,并开始在伦敦科学界和社交圈立足。他没有正式的工作,只是公开举办天文学讲座,撰写有关各种数学主题(函数方程、连乘积、数论等)的论文,虽然并不引人注目,但也值得尊敬。他父亲和妻子的家族为他提供了适度的经济资助。
1819 年,巴贝奇访问了法国,获悉法国政府正在实施一个制作对数表和三角函数表的大型项目。数学表格在当时具有相当重要的军事和商业意义,被广泛应用于科学、工程、金融及航海等领域。人们常常声称,数学表格中的错误会导致船只搁浅或桥梁倒塌。
回到英国后,巴贝奇和赫歇尔开始了一个为他们新成立的天文学会制作表格的项目,据说在检查这些表格的过程中,巴贝奇惊叹道:“我真希望这些表格是由蒸汽制成的!”从此,巴贝奇开始了将表格生产机械化的毕生努力。
早在巴贝奇之前,就已经有了机械计算机。帕斯卡(Pascal)在1642 年就制造了一台,我们现在知道,计算工具甚至在古代就有了。但在巴贝奇的时代,这样的机器还只是稀奇古怪的东西,在日常实际应用中还不够可靠。表格是通过人工计算制成的,计算工作被分派给一个团队中的成员来完成,最低级的计算基于使用差分法对多项式(例如级数展开式)进行求值。巴贝奇设想的是有一种差分机器,可以用差分法来计算任意次数的多项式,然后自动逐步求值并打印结果,完全排除了人类容易出错的倾向的干扰。
1822 年初,30 岁的巴贝奇忙于研究不同类型的机械,并制订设计了差分机的计划和原型。他参与创立的伦敦天文学会(后成为皇家天文学会)为他的这个想法颁发了一枚奖章。1823 年,英国政府同意为建造这样一台机器提供资金支持。
1824 年,巴贝奇因有望加入一家初创的人寿保险公司而稍有分心,他为此做了一系列生命表的计算。但他在自己的马棚(他的“车库”)里设立了一个工作室,不断萌生关于差分机,以及关于如何利用当时的工具制造它的组件的构想。
1827 年,巴贝奇终于完成了手工计算的对数表,并在近 100 年的时间里不断重印。巴贝奇把它们印在黄色的纸上,理论上这样可以减少用户出错。(在我上小学的时候,对数表仍然是做乘法运算的快速方法。)
同样是在 1827 年,巴贝奇的父亲去世,留给他大约 10 万英镑,大致相当于今天的 1400 万美元,这为巴贝奇的后半生奠定了坚实的经济基础。不过,同年,他的妻子也去世了。她和巴贝奇共养育了 8个孩子,但只有 3 个活到了成年。
巴贝奇因妻子的去世而消沉,他去了欧洲大陆旅行,并对他在那里所见到的科学成就印象深刻,于是写了一本名为《对英国科学衰落的反思》(Reflections on the Decline of Science in England)的书,结果该书内容主要是对英国皇家学会(他是其中的一员)的抨击。
虽然经常分心,但巴贝奇仍在继续研究差分机,写下了数千页的笔记和设计稿件。在起草计划或在机器车间做实验时,他总是亲力亲为。但在管理他雇用的工程师方面,他却完全不插手,而且他对成本的管理也不甚理想。尽管如此,到 1832 年,一台小型差分机(不带打印机)的工作原型已经成功完成。这就是埃达·洛夫莱斯在1833 年 6 月所看到的机器。
说回埃达
埃达与差分机的邂逅似乎点燃了她对数学的兴趣。她结识了拉普拉斯(Laplace)的译者以及著名的科学解说者玛丽·萨默维尔(Mary Somerville),并在她的鼓励下,很快热衷于研究欧几里得。1834 年,埃达随母亲参加了一次慈善之旅,访问了英格兰北部的工厂,对当时的高科技设备产生了浓厚的兴趣。
在回来的路上,埃达教了她母亲一位朋友的女儿一些数学知识。她通过信件继续教学,并指出这可能是“两位贵族女士之间长达数年的‘感性数学通信的开始’,毫无疑问将来会出版,以启迪人类”。这并不是什么高深的数学,但埃达说得很清楚,而且还带有这样的告诫:“当可以给出直接证明时,你不应该选择间接证明。”(在埃达的所有手写信件中,有很多下划线,本书以黑体显示这部分文字。)起初,巴贝奇似乎低估了埃达,他试图将埃达的兴趣引到他用作聚会谈资的银娘子(Silver Lady)自动人偶上(并指出,他给人偶加了一块头巾)。但(用她自己的话说)埃达继续与巴贝奇先生和萨默维尔夫人单独或一起互动。很快,巴贝奇就向她敞开了心扉,谈起了许多知识性的话题,也谈起了他在差分机的经费问题上与政府产生的矛盾。
1835 年春天,19 岁的埃达遇到了 30 岁的威廉·金(William King,或者更准确地说,是威廉·金勋爵)。他是玛丽·萨默维尔儿子的朋友,曾就读于伊顿公学(150 年后我也在同一所学校就读)和剑桥大学,后来当过公务员,后期大部分时间在英国位于希腊的一个前哨站工作。尽管威廉有些呆板,但他似乎是一个严谨、认真、正派的人。无论如何,埃达和他一见钟情,他们于 1835 年 7 月 8 日结婚。埃达直到最后一刻才公布这则消息,避免了花边新闻的骚扰。
在接下来的几年里,尽管埃达也有一些时间骑马、学习竖琴和数学(包括球面三角学等主题),但她的生活似乎主要是照顾三个孩子和管理繁重的家务。1837 年,英国维多利亚女王(时年 18 岁)即位,作为上流社会的一员,埃达与她见了面。1838 年,威廉因在政府工作而被封为伯爵(即洛夫莱斯伯爵,Earl of Lovelace),而埃达则成为洛夫莱斯伯爵夫人(Countess of Lovelace)。
1839 年,在她第三个孩子出生后的几个月里,埃达决定重新认真对待数学。她告诉巴贝奇,她想在伦敦找一个“数学导师”,但要求巴贝奇在打听时不要提到她的名字,大概是担心社会上的流言蜚语。
这个导师就是奥古斯塔斯·德·摩根(Augustus De Morgan),伦敦大学学院的第一位数学教授,著名逻辑学家,写过几本教科书,他不仅是巴贝奇的朋友,也是埃达母亲童年时期主要老师的女婿。(是的,世界真小,德·摩根也是乔治·布尔的朋友,是他间接促成了布尔代数的发明。)
在与巴贝奇的通信中,埃达表现出了对离散数学的兴趣,例如,她想知道纸牌接龙游戏(solitaire)是否“可以用数学公式来求解”。但按照当时(如今也还是如此)的数学教育传统,德·摩根让埃达从学习微积分开始。
埃达写给德·摩根的关于微积分的信与今天的微积分学生的信别无二致,只是她用了维多利亚时代的英语。尽管埃达对微积分的糟糕符号更为敏感(比如“为什么不能用 dx 做乘法?”),但她的许多困惑甚至与今天的学生都是一样的。埃达是一名坚持不懈的学生, 似乎很享受不断学习数学的过程。她对自己的数学能力感到高兴, 并对德·摩根给予的积极反馈感到满意。
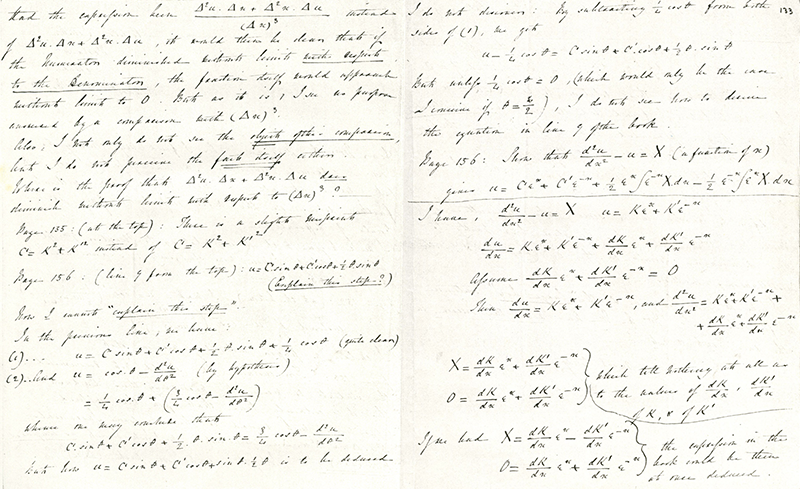
埃达向德摩根学习的笔记丨图片来源:多年来,埃达的健康状况时好时坏,但到了 1841 年,她的健康状况明显恶化,她开始系统地服用阿片制剂。她非常渴望在某些方面有所建树,并开始萌生这样的想法:自己也许应该选择音乐和文学,而不是数学。但她的丈夫威廉似乎说服了她,到 1842 年底,她又重新开始学习数学。
给巴贝奇的“论文”做注释
当这一切发生的时候,巴贝奇又在做什么呢?他一直在做各种各样的事情,取得了不同程度的成功。
相比于一台只会计算差分的机器,他构思了一台“分析机”,支持一系列可能的运算,实际上可以按照任意编程的顺序进行运算。起初,他只是想让机器对固定的公式求值,但随着对不同使用案例的研究,他增加了其他功能,比如条件运算,并常常想出一些非常巧妙的方法来机械地实现这些运算。最重要的是,他想出了如何使用打孔卡片来控制计算步骤,这种卡片是雅卡尔(Jacquard)于 1801 年发明的,用于指定织布机上的编织图案。
巴贝奇创造了一些极为复杂的设计,在今天看来,它们能够正常运行就已经十分了不起了。但早在 1826 年,巴贝奇就发明了一种他称之为机械符号的东西,旨在为机械运算提供一种符号表示,就像数学符号为数学运算提供一种符号表示一样。
早在 1826 年的时候,巴贝奇就已经对没人赏识他的发明而失望了。毫无疑问,人们当时并不理解它,因为即使是现在,也没人能搞清楚它是如何工作的。但这可能是巴贝奇最伟大的发明,因为很显然,正是这项发明催生了他所有的精心设计。
巴贝奇最初的差分机项目耗费了英国政府 17 500 英镑,大约相当于今天的 200 万美元。与政府的其他开支相比,这只是一笔小数目,但这个项目非同寻常,引起了相当多的讨论。巴贝奇喜欢强调,与和他同时代的许多人不同,他本人并没有拿过政府的钱(尽管他把自己的马棚装修成防火车间等都要花钱)。他还声称,他最后差不多在各种项目上花了自己 2 万英镑,或者说是他大部分财产(我并不明白这些数是怎么加起来的)。他还不断努力争取政府的进一步支持,并制定了建造差分机 2 号的方案,该方案只需要 8000 个零件,而不是 25 000 个。
到 1842 年,政府人事已经更迭,巴贝奇坚持要与新首相(罗伯特·皮尔,Robert Peel)会面,但最终被新首相痛斥了一番。在议会上,给差分机提供资金的想法最终被诸如“机器要能够进行计算才算有点儿用”的讥讽叫停了。
巴贝奇的想法虽然在英国得不到支持,但在其他地方却受到了一定欢迎。1840 年,巴贝奇应邀到意大利都灵就分析机这一主题做了演讲,并获得了意大利政府的嘉奖。
巴贝奇从未发表过关于差分机的正式报告,也从未发表过任何关于分析机的文章。但他在都灵谈到了分析机,一个名叫路易吉·梅纳布雷亚(Luigi Menabrea)的人做了笔记,当时他还是一位 30 岁的陆军工程师,但 27 年后,他成了意大利王国的首相(还对结构分析数学做出了贡献)。
1842年10月,梅纳布雷亚根据自己的笔记用法语发表了一篇论文。埃达看到这篇论文后,决定将其翻译成英文,并投稿给英国的一家出版社。许多年后,巴贝奇声称他曾建议埃达撰写自己关于分析机的说明,而她回应说自己并没有过这个想法。但无论如何,到 1843 年2 月,埃达已决心完成翻译工作,但要加上她自己的大量注释。
在随后的几个月里,她非常努力地工作,几乎每天都与巴贝奇通信(尽管有时还有其他“紧迫且无法回避的约会”)。埃达向巴贝奇提问,巴贝奇回答,她找到方案,巴贝奇提出意见。显然是她在主导,但她认为自己首先是在解释巴贝奇的工作,因此希望与巴贝奇一起核对确认。不过,当巴贝奇试图修改她的手稿时,她会感到恼火。
埃达在调试伯努利数的计算时写下了这样一封信,真是引人入胜:“亲爱的巴贝奇,这些数让我陷入了令人震惊的泥潭和麻烦之中,我为此感到非常沮丧,以至于我今天不可能完成这件事。……我现在要出去骑马了。”后来,她告诉巴贝奇:“我整天都在不停地工作,而且非常成功,您一定会非常欣赏这些图表。它们都是我极其精心制作出来的,所有的指数都得到了最细致和最严谨的处理。”然后她补充说,威廉(或她口中的“L. 勋爵”)“此刻正在亲切地为我把这一切都涂上墨水。我不得不用铅笔来写……”。
威廉显然也是建议她在译文和注释上签名的人。正如她在写给巴贝奇的信中所说的那样:“我并不想宣布这本书是谁写的。同时,我更希望附上一些东西,以便日后将它与所谓的 A.A.L.(即 Ada Augusta Lovelace,埃达·奥古丝塔·洛夫莱斯)的其他作品区分开来。”
到 1843 年 7 月底,埃达几乎完成了她的注释写作。她为这些注释感到骄傲,巴贝奇也对它们赞不绝口。最后,埃达的译文出现了,署名为“AAL”。
后来,她的健康状况急转而下,她花了好几个月去看医生并尝试各种“疗法”不过,她仍然对科学充满激情。她与迈克尔·法拉第有过交往,据说法拉第称她为“科学界的新星”。当她的注释发表时,巴贝奇曾说:“你应该写一篇原创的论文,即便推迟发表也只会使它更加完美。”
再后来,埃达的健康状况就变得非常糟糕。有一段时间,医生只是让她多去海边走走,但他们最终承认她得了癌症(从我们现在所知道的情况来看,很可能是宫颈癌)。阿片不再能控制她的疼痛,她开始尝试大麻。到了 1852 年 8 月,她写道:“我开始理解死亡,它每时每刻都在悄悄地、逐渐地进行着,永远不会是某个特定时刻的事情。”8 月 19 日,她邀请巴贝奇的朋友查尔斯·狄更斯来访,狄更斯为她朗读了自己一本书中关于死亡的描述。
巴贝奇在埃达去世后又活了 18 年,于 1871年去世。1856 年,他再次尝试研究分析机,但没有取得重大进展。
重新发现
巴贝奇去世后,他在他的机器方面的毕生工作几乎被人遗忘了(尽管 1911 年的《不列颠百科全书》等还有提及)。尽管如此,机械计算机仍在继续发展,逐渐让位于机电计算机,最终被电子计算机 所取代。20 世纪 40 年代,当人们开始理解编程时,巴贝奇的工作和埃达的注释被重新发现。
人们知道“AAL”代表埃达·奥古丝塔·洛夫莱斯,她是拜伦的女儿。艾伦·图灵读过她的注释,并在 1950 年的图灵测试论文上 创造了“洛夫莱斯夫人的异议”(Lady Lovelace’s Objection,即“人 工智能无法创造任何东西”)这个术语。但在当时,埃达本人在很大程度上还只是一个脚注。
一位名叫伯特伦·鲍登(Bertram Bowden)的英国核物理学家进入了计算机行业,最终成为英国科学和教育部部长,是他“重新发现”了埃达。在为他 1953 年出版的《比思考更快》(Faster Than Thought,没错,是关于计算机的)一书做研究时,他找到了埃达的外孙女温特沃思夫人,她向他讲述了关于埃达的家族传说,有准确的,也有不准确的,并让他看了一些埃达的论文。有趣的是,鲍登注意到,在埃达的外孙女的《纯种赛马》(Thoroughbred Racing Stock)一书中,使用了二进制来计算血统。当然,埃达和分析机所使用的是十进制,还没有考虑二进制。
但即使是在 20 世纪 60 年代,巴贝奇和埃达也并不出名。巴贝奇的差分机原型曾被赠送给伦敦的科学博物馆,我在 20 世纪 60 年代还是个孩子时经常去科学博物馆,我很确定我从来没有在那里看到过它。不过,到了 20 世纪 80 年代,特别是在美国国防部以埃达的名字为其命运多舛的编程语言(即Ada语言)命名之后,人们对埃达·洛夫莱斯和查尔斯·巴贝奇的认识开始增加,传记也开始出现,不过有时会出现一些匪夷所思的错误(我最喜欢的是,有人提到,在巴贝奇的一封信中提到的“三体问题”表明巴贝奇、埃达和威廉之间存在三角感情关系,而它实际上指的是天体力学中的三体问题!)。
随着人们对巴贝奇和埃达的兴趣与日俱增,人们也越来越好奇,如果按照巴贝奇的计划建造差分机,它是否真的能够工作。2002 年,一个项目启动了,经过艰苦的努力,一台完整的差分机被制造了出来,只对方案做了一处修正。令人惊讶的是,这台机器居然真的可以运行。考虑通货膨胀因素,建造这台机器的成本与巴贝奇在 1823年向英国政府提出的要求大致相同。
那分析机呢?到目前为止,还没有一台真正的分析机被制造出来,甚至没有完全模拟出来。
埃达究竟写了什么
埃达关于分析机的注释的实际内容又是什么呢?
它的开头很清晰:“差分机是用来计算特定函数的积分并制作表格的,该函数是……”她接着解释说,差分机可以计算任何六次多项式的值,但分析机则不同,因为它可以执行任何运算序列。或者,正如她所说:“分析机是运算科学的具体体现,它在构建时特别参考了抽象的数作为运算对象。而差分机则是一组特定且非常有限的运算的具体体现……”
考虑到我在 Mathematica 上花了这么多年的时间,至少对我来说,令人高兴的是,她在后面的一段话中继续说道:“我们可以将机器视为分析的物质和机械代表,通过机器我们能够完全控制代数和数值符号的执行运算,从而使我们在人类研究的这一领域的实际工作能力,比以往更有效地跟上我们对其原理和法则的理论认识。”
稍后,她又解释说,打孔卡片是控制分析机的方式,然后她发表了一个经典声明:“分析机编织代数模式,就像雅卡尔提花机编织花朵和叶子一样。”
然后,埃达详细介绍了一系列特定类型的计算如何在分析机上工作,其中“运算卡片”定义了要执行的运算,“变量卡片”定义了值的位置。埃达谈到了“循环”和“循环的循环”等,也就是现在所说的循环和嵌套循环,并给出了相应的数学符号: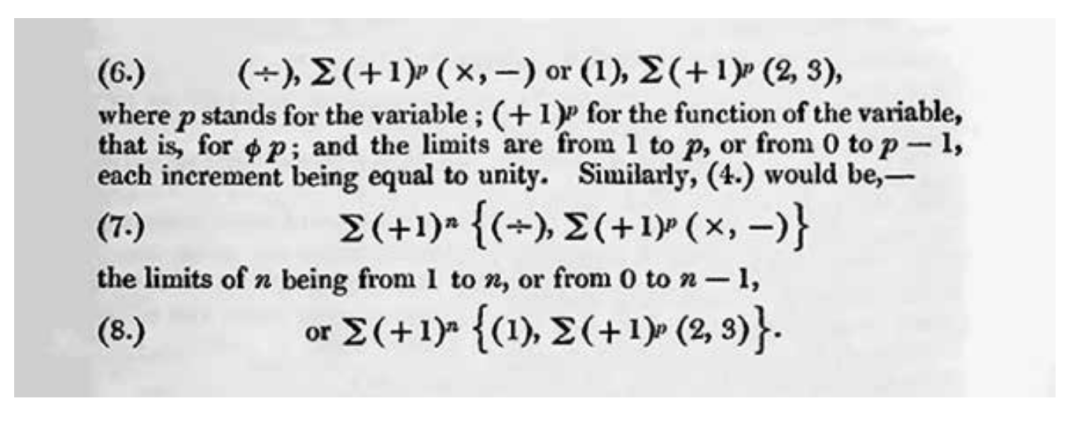 在埃达的注释中有很多看起来很现代的内容。她评论说:“有一幅美丽的雅卡尔提花机编织的画像,制作它需要 2.4 万张卡片。”然后,她讨论了使用循环来减少所需卡片数量的想法,以及重新排列运算以优化其在分析机上的执行的价值,最终表明只需 3 张卡片就能完成看似需要 330 张卡片才能完成的工作。
在埃达的注释中有很多看起来很现代的内容。她评论说:“有一幅美丽的雅卡尔提花机编织的画像,制作它需要 2.4 万张卡片。”然后,她讨论了使用循环来减少所需卡片数量的想法,以及重新排列运算以优化其在分析机上的执行的价值,最终表明只需 3 张卡片就能完成看似需要 330 张卡片才能完成的工作。
埃达谈到了分析机在计算以往无法计算的东西方面所能达到的程度,至少在精确度上是如此。作为例子,她讨论了三体问题,以及在她那个时代,在“大约 295 个月球摄动系数”中,许多系数经由不同的人计算所得的结果并不一致。
最后是埃达的注释 G。她早期就说过:“分析机并不自诩能创造任何东西。我们知道如何命令它做什么,它就能做什么。……它的职责是帮助我们了解我们已经熟悉的东西。”
埃达似乎对编程的传统观点有了较为清晰的理解:我们设计程序来做我们知道如何做的事情。但她也指出,在实际把“真理和分析公式”变成一种适合机器的形式时,“这门科学中许多主题的性质必然会被置于新视角,并得到更深刻的研究”。换句话说,正如我经常指出的那样,实际上编程不可避免地会让人对其进行更多的探索。
她接着说:“在为数学真理设计一种新的形式来记录和投入实际使用时,很可能会引发一些观点,而这些观点又可能会对这门学科更为理论的阶段产生影响。”或者换句话说,正如我经常说的那样,以可计算的形式来表示数学真理可能有助于人们更好地理解这些真理本身。
不过,埃达似乎明白,由机器所实现的“运算科学”不仅适用于传统的数学运算。例如,她指出,如果“和声学中音高的基本关系”可以进行抽象运算的话,那么机器就可以利用它们“创作出任何复杂程度或范围的精致而科学的音乐作品”。对于 1843 年来说,这样的理解水平还不错。
伯努利数的计算
在埃达所写的文章中,最著名的部分是注释 G 中关于伯努利数的计算。这似乎源于 1843 年 7 月她写给巴贝奇的一封信。她在信的开头写道:“我很努力地为你工作着。事实上,我就像魔鬼一样(也许我就是魔鬼)。”然后,她要求巴贝奇提供一些具体的参考资料。最后她说:“我想在我的一处注释中加入一些关于伯努利数的内容,作为一个例子,说明如何通过机器计算出隐函数,而无须先通过人的头脑和双手计算出来……。请你给我必要的数据和公式。”
埃达用伯努利数来展示分析机是一个有趣的选择。早在17世纪,人们耗费毕生的时间来制作整数幂和的表格,换句话说,列出不同m和n的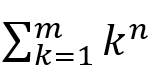 值。但雅各布·伯努利(Jacob Bernoulli)指出,所有这些和都可以表示为 m 的多项式,其系数与现在所谓的伯努利数有关。1713 年,伯努利自豪地说,他“在 15 分钟内”计算出了前10 个伯努利数,再现了其他人多年的工作成果。
值。但雅各布·伯努利(Jacob Bernoulli)指出,所有这些和都可以表示为 m 的多项式,其系数与现在所谓的伯努利数有关。1713 年,伯努利自豪地说,他“在 15 分钟内”计算出了前10 个伯努利数,再现了其他人多年的工作成果。
当然,今天用 Wolfram 语言进行计算是可以瞬间完成的: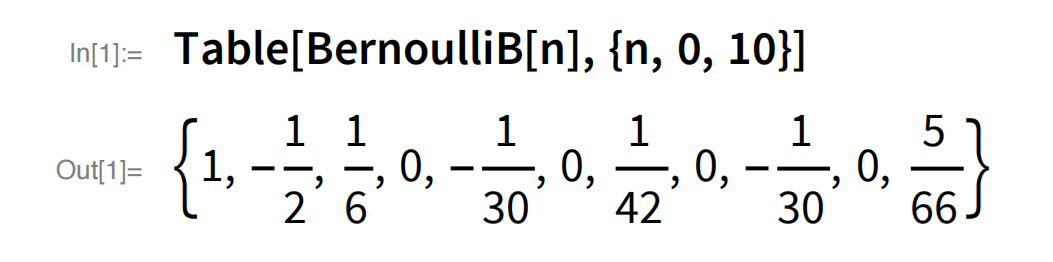 碰巧的是,几年前,为了展示新的算法,我们甚至计算了 1000 万个伯努利数。
碰巧的是,几年前,为了展示新的算法,我们甚至计算了 1000 万个伯努利数。
那么,埃达打算怎么做呢?她从伯努利数出现在级数展开式中这样的事实出发:
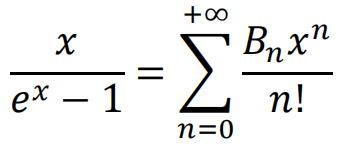
然后,通过重新排列并匹配 x 的幂次,她得到了一系列伯努利数Bn的方程,然后她将其“展开”,得到了一个递推关系式:
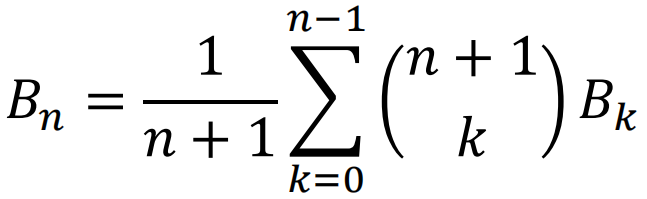 现在埃达必须说明如何在分析机上实际计算这个问题。首先,她利用(除 B1 外的)奇伯努利数为零的事实计算出 Bn ,即我们现代的 B2n(或 BernoulliB[2n])。然后,她从 B0 开始,对较大的 n依次计算 Bn ,并存储每个结果。她用于计算的算法(用现代方法来描述)是 :
现在埃达必须说明如何在分析机上实际计算这个问题。首先,她利用(除 B1 外的)奇伯努利数为零的事实计算出 Bn ,即我们现代的 B2n(或 BernoulliB[2n])。然后,她从 B0 开始,对较大的 n依次计算 Bn ,并存储每个结果。她用于计算的算法(用现代方法来描述)是 :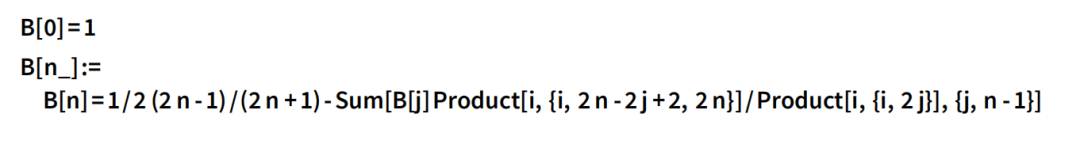
(编者注:这里用 Wolfram 语言对这一算法进行了说明。“B[n]”表示伯努利数 Bn ,“Sum”和“Product”分别为求和与连乘。这段代码首先指定伯努利数第一项为 1,然后定义了一个用于求伯努利数的递归函数。)
在分析机上,我们的想法是进行一系列由“磨坊”来执行的运算(由运算卡片指定),这些运算数来自“仓库”(Store,即存储单元,地址由变量卡片指定)。(在“仓库”中,每个数由一系列轮子表示,每个轮子转到每位数字的对应值。)以埃达想要的方式计算伯努利数需要两个嵌套的循环运算。在当时的分析机设计下,埃达基本上不得不展开这些循环。但她最终成功地描述了如何计算 B8(她称之为 B7 ):
这实际上是在分析机上运行程序的执行轨迹,共 25 步(加一个循环)。在每一步中,轨迹显示了对哪些变量卡片执行了哪些运算,以及哪些变量卡片收到了运算结果。由于缺乏循环的符号表示,埃达只能使用大括号在执行轨迹中表示循环,并用英语指出重复的部分。
最后,计算的最终结果出现在位置 24 上: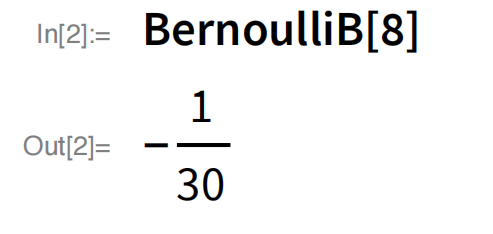
正如打印出来的那样,埃达的执行轨迹在第 4 行出现了一个错误:分数上下颠倒了。但如果修正了这个错误,就可以很容易地得到一个现代版的埃达算法。正如埃达所指出的那样,计算更靠后的伯努利数最终并不需要更多的工作变量(由变量卡片指定),只需要更多的运算。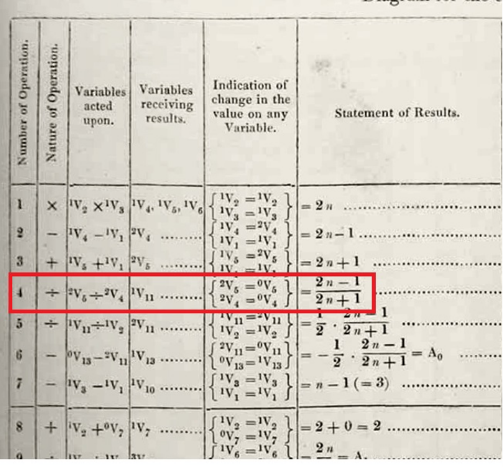
1843 年设计的分析机应该可以存储 1000 个 40 位数,原则上可以计算到 B50 ( = 495 057 205 241 079 648 212 477 525 / 66 )。它的速度也相当快,其设计目标是每秒进行约 7 次运算。所以埃达的 B8运算大概花了 5 秒钟,而 B50 运算可能需要 1 分钟。
奇怪的是,即使在几年前我们创纪录的伯努利数计算中,我们使用的算法也基本上与埃达相同,尽管现在有了稍微快一点的算法,可以有效地计算伯努利数的分子对一系列质数进行模运算的结果,然后使用中国剩余定理(也称孙子定理、中国余数定理)重构完整的数。
巴贝奇 vs 埃达?
分析机及其构造都是巴贝奇的工作。那么埃达又补充了什么呢?埃达认为自己首先是一个阐释者。巴贝奇曾给她看了很多分析机的图纸和例子。她想解释它们的总体要点是什么,并将其与“宏大、概括和形而上学的观点”联系起来。
在现存的巴贝奇论文档案(多年后在其律师家的牛皮行李箱中被发现)中,有大量关于分析机的阐述草稿,这些草稿从 19 世纪30 年代开始,一直持续了几十年,标题包括《关于分析机》(“Of the Analytical Engine”)和《将数的科学归约为机械》(“The Science of Number Reduced to Mechanism”)。我们尚不清楚为什么巴贝奇从未发表过这些作品。它们似乎是对分析机基本运作原理的完美描述,尽管与埃达的作品相比,这些描述无疑更加乏善可陈。
巴贝奇去世时,他正在写一本关于分析机的历史的书,他的儿子完成了这本书[编者注:他的儿子即前文提到的亨利·巴贝奇,最终成书为《巴贝奇的计算机器》(Babbage's Calculating Engines)]。在这本书中,有一份注明日期的清单,列出了“446 种分析机符号”,每一种符号基本上都代表了如何在分析机上进行某种运算,比如除法。日期从 19 世纪 30 年代开始,一直持续到19 世纪 40 年代中期,其中 1843 年夏天列示的符号并不多。
同时,在英国科学博物馆收藏的巴贝奇的论文中,有一些关于分析机的更高级运算的草图。例如,1837 年的草图中,有“两个一阶方程之间的消元”,这本质上是对有理函数的求值。
但是,没有任何一项工作能像埃达对伯努利数的计算那样复杂或清晰了。巴贝奇当然对埃达的工作有所帮助和评论,但埃达绝对是这项工作的推动者。
埃达对分析机应该具备的能力有了想法,并向巴贝奇提出了如何实现这一目标的问题。根据我自己与现代硬件设计师打交道的经验,这些问题的答案往往会非常详细。埃达的成就是从这些细节中提炼出对机器抽象运算的清晰阐述,而这是巴贝奇从未做过的。(在他的自传中,他基本上只是提到了埃达的注释。)
更广阔的图景
埃达·洛夫莱斯是一位聪明的女性,她和巴贝奇成了朋友(没有任何证据表明他们曾经有过恋情)。出于对巴贝奇的帮助,她写了一篇关于分析机的阐释,在此过程中,她对分析机有了比巴贝奇更抽象的理解,并窥见了通用计算这一令人难以置信的强大思想。
当埃达写到巴贝奇的机器时,她想用最清晰的方式解释它的功能。为此,她对机器进行了更抽象的研究,结果是她最终探索并阐明了现代通用计算一些很容易被识别的概念。
埃达所做的一切被遗忘了很多年。但随着数理逻辑领域的发展,通用计算的概念再次出现,最明显的是艾伦·图灵在 1936 年的工作。然后,在 20 世纪 40 年代,当电子计算机被制造出来时,人们意识到它们也表现出了通用计算的特性,并将其与图灵的工作联系起来。
埃达接触到了在我们这个时代具有决定性意义的知识思想,这是一种幸运。巴贝奇不知道自己拥有什么,而埃达则看到了一些蛛丝马迹,并成功地描述了它们。
作者简介

斯蒂芬·沃尔弗拉姆(Stephen Wolfram):计算机科学家、数学家和理论物理学家。他创造了在全世界备受推崇的软件系统——Mathematica、Wolfram|Alpha和Wolfram语言。35年来,他一直担任科技公司Wolfram Research的首席执行官,并取得了基础科学领域的一系列突破性进展,包括最近的Wolfram物理项目(Physics Project)。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 