撰文 | 孟子杨

 

来源 | 选自《物理》2020年第11期

 

引 子

 

有的童话穿越历史，变成了一个民族心中的文化图腾，如西游记之于中国人，安徒生和格林童话之于欧洲人。有的童话停留的时间稍短，但也是一代人甚至几代人心中共同的启蒙故事，如《星际旅行》、《铁臂阿童木》、《机器猫》甚至《哈利波特》。对中国的孩子来说，尤其是在1980年代至1990年代成长起来的孩子，这样的童话应属皮皮鲁和鲁西西的故事了。这些故事填补了彼时孩子们十分枯燥和闭塞的学校教育的空白 (现在也许不闭塞了，但是否枯燥不得而知)，让他们感受到了想象力的震撼和独立思考带来的乐趣。现在回头看，皮皮鲁和鲁西西的那些奇遇从技术上讲十分落伍，在科学上有的更是完全不合理，当然也无法和现在的硬核工业党穿越科幻相比，但是皮皮鲁和鲁西西好就好在不按照彼时学校里和社会上灌输给孩子们的教条行事，总爱搞些小玩闹、小探索，却总能在无意中发现一个新的世界，让彼时的孩子们知道，好奇心和对不公正的一点点小反抗不但不是罪恶，反而是特别正确和特别好玩的事，在特立独行和无拘无束中才能学会真正的同情心和责任感。

 

一晃几十年过去，彼时的孩子都长成了大人，他们中有人也开始教育自己的孩子按照当下学校里和社会上的教条行事，而他们自己也努力地学着当下社会上的通行规范，扮演着一个好员工、好同事、好下属、好老师或者好领导的角色，童话嘛，毕竟是要远去的。但是大家偶尔想起皮皮鲁和鲁西西，又似乎心有不甘，想着毕竟什么时候还是要做出一些像他们那样出格的、有趣的事情，尝试一些与众不同的、能够发现新的世界的探索，人生才不算白过。若是有人完全忘记了皮皮鲁和鲁西西，那么这样的人要么是对自身彻头彻尾的失望者，要么就是在当下社会中彻头彻尾的成功者。

 

在笔者熟悉的量子多体计算领域，就有一群这样不能忘情的人，还总想着皮皮鲁和鲁西西，总喜欢玩些在行业内的正人君子们、行业内的成功者们看来离经叛道，吃力不讨好的游戏。好在他们自己觉得有趣，在这样的玩闹中自己的好奇心和求知欲得到了极大的满足，并且渐渐开始影响和鼓励着身边的朋友们。最近就有这样一个故事，这几个童心未泯的小伙伴，用蒙特卡洛和张量重正化群的计算方法，完成了好几个好玩的计算，还鼓动着实验物理学家们验证了他们的结果，实验的伙伴们更发现了有趣的新问题。大家就这样一路乐此不疲地玩下去。

 

下面就是他们的故事，为了讲好这个故事，为了向皮皮鲁和鲁西西致敬，姑且称这样一群人都是蒙蒙卡和张量量吧。

 

蒙蒙卡与张量量探索量子材料

 

量子材料研究是很好玩的事情，因为量子材料是一个很大的筐，什么东西都放得进去：从超越摩尔定律的新一代集成电路人工智能芯片材料，到具有解决能源危机潜力的高温超导体，还有现在十分流行的转角石墨烯二维范德瓦尔斯层状材料，再到希望成为量子计算机信息存储载体的拓扑物态，都算量子材料的内容。但是对于这些材料性能的研究需要严格处理其中阿伏伽德罗常数量级的满足量子物理学规律的电子行为(因此这类问题也被称为量子多体问题)，计算量子多体系统在温度、压力和磁场等外界环境变化时的响应，从而确定其在科研和工业应用中合适的参数范围。这样复杂的问题已经不是铅笔和白纸般古典时代的推算可以解决得了，很多时候以微扰论为基础平均场计算甚至不能提供定性正确的结果，遑论定量。取而代之的，大规模量子多体计算方法，伴随着全球范围内计算平台的迅猛发展和普及，辅之以场论、对称性和拓扑性质分析等高级数学语言的应用，逐渐成为现代物理、化学、材料科学的主流研究方式，使得科学家和工程师们可以不断地发现具有更加优异性能的材料，拓展量子物质科学的内涵和外延，造福人类生活。

 

在量子多体计算研究这个广大的领域之中，量子蒙特卡洛方法 (是为蒙蒙卡) 和张量重正化群方法 (是为张量量)，无疑是两种最具有代表性的手段。前者及其最近的发展笔者在这个系列的前几篇文章中已反复介绍过，主要是通过设计抓住问题物理实质的晶格模型，然后在如是模型的合适相空间中进行蒙特卡洛抽样，计算量子多体问题的配分函数和各种物理观测量的系综平均值和误差。而后者则一路从密度矩阵重正化群演化而来 (见参考文献，哦不对，见蒙蒙卡和张量量迷宫地图之[1])，主要关注于量子多体基态波函数的张量网络表示与其重正化群操作。

 

当然，传统的蒙蒙卡和张量量研究，主要还是专注于量子多体模型性质的计算，比如Hubbard模 型，t—J模型，Heisenberg模型，还有之前在这个系列中提到的费米子—玻色子耦合模型。如果严格计算真实量子材料的性质，考虑到材料本身的复杂性(多种相互作用和晶格的物理、化学环境所带来的指数墙问题)，即使对于蒙蒙卡和张量量这样充满活力的小伙伴，大多数时候也无能为力。但是问题有意思的地方就在于是否敢于尝试，敢于特立独行不按教条行事，找到走出迷宫的神秘地图，这里的故事就是一个成功的事例 (见蒙蒙卡和张量量迷宫地图之[2，3])。

 

这次蒙蒙卡和张量量面对的问题是如何“破译”二维阻挫磁性晶体TmMgGaO4(TMGO)的“材料基因”，即得到这样材料体系的正确微观模型和模型中的参数。材料的示意图如图1，晶格结构为三角晶格，通过物理和化学结构的分析，人们认为三角晶格量子伊辛模型似乎是一个合适的出发点，但是问题是精确模型参数该如何得到？这里张量量发挥了很大的作用。一直以来，在张量重正化群领域中，人们普遍地喜欢开发新的方法，从DMRG，TMRG到后面的LTRG，CTMRG，PEPS，iDMRG，TEBD，METTS，SETTN等等，不一而足，让外行人看得眼花缭乱、一头雾水，只见业内专家们口吐莲花般抛出许多新名词与它们的骨感缩写。其实领域内部大家主要还是关注量子多体模型基态波函数的张量表示，以及为了达到某种精度在张量的数值操作上如何降低计算复杂度等等。但在外人看来，这个领域就显得对于实际量子材料系统的热力学和动力学性质关注比较少，也就很难和行业之外的物理学家(如实验物理学家)进行实质性的沟通。

图1 磁性晶体TMGO中的电子自旋排布与磁振子—涡旋对激发(见蒙蒙卡和张量量迷宫地图之[2，3])

 

但还是有特立独行的人，此次张量量小伙伴们是来自北京航空航天大学物理学院的李伟老师和他的研究生李涵和陈斌斌等，他们与合作者独辟蹊径，开发出了指数热态张量网络方法 (Exponential ThermalTensor Network，XTRG，虽说又多了一个名字……)，但这个方法可以在尽量保持计算结果精度的情况下，得到量子多体系统的热力学信息 (细节见迷宫地图之[7])。然后他们运用XTRG计算了TMGO模型系统的比热、磁化率和磁矩等物理可观测量随着温度和磁场变化的行为，再通过与实验结果进行对比和调整模型参数，最终得到了TMGO的正确晶格模型——三角晶格量子伊辛模型及其精确模型参数。如图2所示，XTRG算出的熵、比热、磁化率和磁矩可以在很宽的温度范围内完美地拟合实验观测的磁比热、熵曲线、磁化曲线等诸多磁热力学性质。

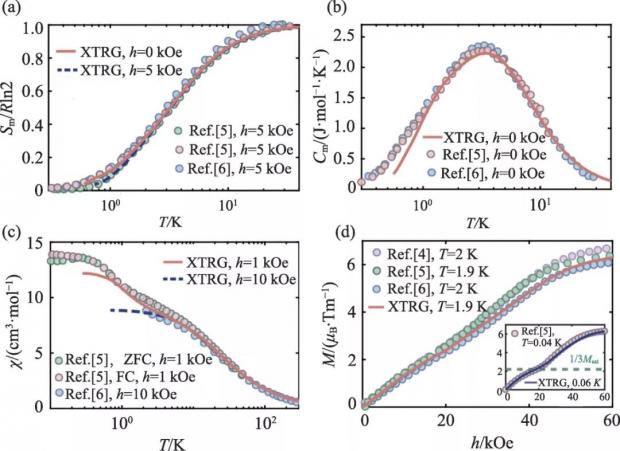
图2 热态张量网络多体计算精确拟合TMGO磁热力学测量数据

 

得到了材料的微观模型之后，小伙伴中的真∙理论物理学家复旦大学戚扬老师略作沉思，口占一偈道，“籍此三角晶格量子伊辛模型，磁性晶体TMGO将在特定的温度范围内展现出奇异的拓扑Kosterlitz—Thouless(KT)相”。鉴于戚老师讲话常常暗含玄机，此处笔者不得不写下一个按语，原来Kosterlitz与Thouless是2016年诺贝尔物理学奖得主，是次诺奖颁发给拓扑物态的三位开拓者，其中Kosterlitz与Thouless在1970年代便预言了量子磁性材料中可能存在的拓扑相，即现在用他们名字命名的KT相。此前人们在二维超流体和超导体中已经观察到KT相，但是经过半个世纪的寻找，KT相在量子磁性材料中却一直没有找到。戚扬老师掐指一算，口中念念有词，“KT相将会在模型如此如此这般这般的参数范围内出现，下面可以请蒙蒙卡君来为之一决”。

 

蒙蒙卡果然是好样的，如笔者在之前的系列文章中所讲，蒙蒙卡在最近的几年里开始逐渐扬弃如死磕square lattice Hubbard模型等等主流套路，剑走偏锋，捣鼓出很多新的技能，其中一项就是从量子多体系统路径积分的虚时关联函数中，运用随机解析延拓的方法得到系统在频率空间的谱函数[8]。有了张量量给出的精确微观模型，蒙蒙卡计算了如是模型的自旋动力学谱函数，如图3所示，如此的谱函数可以直接和TMGO材料在非弹性中子散射实验中得到的自旋谱函数进行比较。在图3(a)中，可以看到模型计算所得的结果与实验结果完全吻合。不仅如此，蒙蒙卡还确实看到了系统出现KT相的温度范围，并对于在这样温度范围内应该看到的中子散射自旋能谱的色散关系和谱权重分布做了预测，结果如图3(c)。

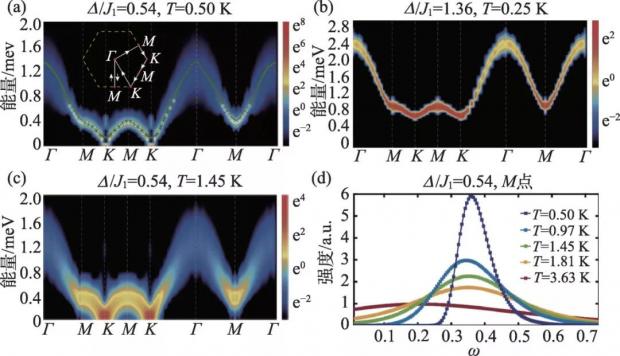
图3 二维自旋阻挫量子磁体TMGO的量子多体蒙蒙卡动力谱学模拟结果。(a)中的数据点为中子散射实验结果，其后的背景为蒙蒙卡计算所得的量子伊辛模型自旋谱函数。(b)，(c)，(d)都是蒙蒙卡在不同模型参数下计算得到的材料自旋能谱

 

成功地得到了材料的微观模型参数并解释了已有的实验结果，大家都觉得“量子磁体真是非常有趣的量子材料，丰富的多体效应中涌现出新奇的量子物态与相变，吸引着我们在其中探寻凝聚态物理的新范式”，虽说开展精确理论计算并与实验对比仍然是量子多体问题亟待解决的前沿问题。但在这项研究中，通过蒙蒙卡和张量量的配合，小伙伴们成功地完成了关联量子晶体材料的热力学—动力学的多体计算。“那么下面一步该去哪里玩耍呢？”有人问到。这时又是戚扬老师给大家指点迷津，“下面咱们去找实验的朋友们，验证已经从理论上得到的结果，如KT相的探测和这种具有准长程序和强烈磁性涨落的奇异物态的其他标度行为，岂不快哉？”，众人皆欢喜不待。

 

蒙蒙卡和张量量找到了实验的伙伴

 

为了能够从实验上看到KT相所特有的磁性涨落，需要十分精密的测量手段，小伙伴们找到了南京大学的温锦生老师和中国人民大学的于伟强老师。温老师那里可以长出单晶样品并完成磁化率在不同温度和磁场下的测量，而于老师组里发展的核磁共振测量正是探测系统磁性涨落的敏感利器。实验小伙伴们听明白了蒙蒙卡和张量量的话，不但欣然应允入伙，而且还发现因为材料中的面内磁矩具有多级矩的性质，通过施加面内磁场刚好就可以收集到材料中 Ga 元素的核磁共振自旋—晶格弛豫率 (行内黑话叫 1/T1)。对于普通的磁性相变，1/T1在相变点会有一个峰出现，代表了相变点上的发散关联长度与丰富的低能涨落。而在如TMGO这样的磁性系统中，从高温的无序顺磁到低温的磁有序相，系统不是经历一个相变，而是要走过一个有限温度的区间，这个区间就是KT相。虽然此处没有长程序，但是系统的关联长度却发散，是一个准长程序的状态。我们不禁要问，在如此状态中1/T1应该是什么样子？

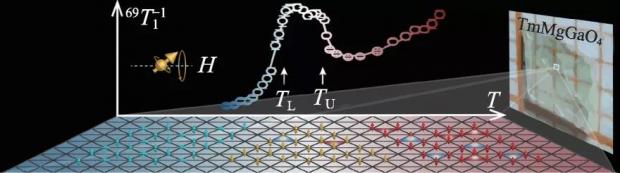
图4 背景为磁性晶体TMGO中KT相的核磁共振信号。下面的平面中示意性地画出在对应的温度范围内，系统处在高温顺磁、中间温度KT相，与低温下的磁有序相的自旋构型。右边的背景为实验生长出的单晶照片

 

实验的结果显示在图4这个示意图的背景中 (顺便说一句，图1和图4这样漂亮的示意图，既有物理内容，又充满艺术气息，都出自张量量之北京航空航天大学物理学院的李涵同学和李伟老师，可见其玩心之大)。随着温度的降低，系统处于顺磁状态，自旋晶格弛豫率随着温度先降低，后开始缓慢抬升，预示着系统内部的磁性涨落在逐步增强；当温度到达KT相的上边界Tu的时候，本要发散的1/T1突然到达一个平台，而在T1<T<Tu的整个温度范围内，自旋晶格弛豫率始终保持在这个高的平台而基本不变，这样的平台就说明系统在这个温度范围内具有很强的磁性涨落，但没有发展出长程序，这正是KT相应该具有的行为。说来有意思，如此的行为，如此的核磁共振1/T1平台信号，还是第一次在磁性晶体中被观测到，着实让众人兴奋了一会儿。

 

这时戚扬老师又口占一偈， “ 籍此实验观测，其实核磁共振的信号我们也可以从蒙卡计算所得的自旋动力学能谱中获得，蒙蒙卡你应该如此如此这般这般，就可以从数据中得到与实验观测类似的物理量，在模型的层次上也抓住系统低能的磁性涨落。汝其为我一决。”蒙蒙卡当下依计行事，果然得到了图5(b)的计算结果，与图5(a)的实验观测定性相似。当然实际的材料总比理论模型复杂，实验中还有很多有趣的细节，如温锦生老师他们测得磁场下系统的磁化率，还可以分析出很多与KT相有关的有趣物理，这些实验的小伙伴们自然会专门撰文解答，在此就不熬述了。细节也都在参考文献 (哦不，蒙蒙卡和张量量迷宫地图之[9]) 中。

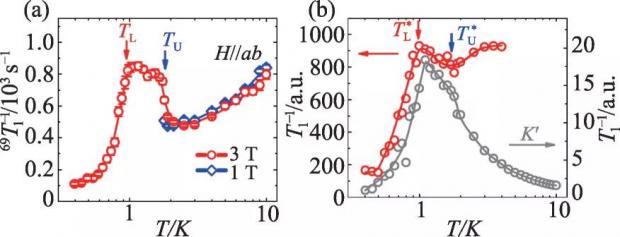
图5 (a)核磁共振实验测得的自旋晶格弛豫率1/T1，其中的平台信号是中间温度KT相；(b)蒙蒙卡在三角晶格量子伊辛中计算的1/T1，不但与实验观测定性吻合，更看出来系统主要的低能磁激发来自于布里渊区中K点附近

 

蒙蒙卡和张量量下面会去何处探险

 

至此，蒙蒙卡和张量量此番量子材料探索行迹已交代清楚，这样无拘无束的探寻让众人尝到了不按教条行事的乐趣。量子多体系统的巍峨群山、森森林海和广阔原野就是他们自由自在驰骋的世界，转角石墨烯、拓扑序的模型与材料实现、非费米液体和量子临界金属……等等胜地都是他们探寻路上行经的风景。也许有一天，他们会来到你的身边，神气活现地给你讲起他们最近的奇遇。这时请耐心听，那其中也许又是新的惊喜，你也许也会按捺不住加入他们的行列的。

 

蒙蒙卡与张量量迷宫地图

 

[1] 刘耘婧，陈斌斌，李伟. 有限温度量子多体系统与热态张量网络. 物理，2017，46(7)：430

 

[2] Li H，Liao Y D，Chen B B et al. Kosterlitz-Thouless melting of magnetic order in the triangular quantum Ising material TmMgGaO4. Nature Communications，2020，11：1111

 

[3] 李伟，孟子杨，戚扬. 二维量子磁体中的“幽灵软模”与KT物理. 物理，2020，49(5)：400

 

[4] Cevallos F A，Stolze K，Kong T et al. Anisotropic magnetic properties of the triangular plane lattice material TmMgGaO4. Mater. Res. Bull.，2018，105：154

 

[5] Li Y et al. Partial up-up-down order with the continuously distributed order parameter in the triangular antiferromagnet TmMgGaO4. Phys. Rev. X，2020，10：011007

 

[6] Shen Y et al. Intertwined dipolar and multipolar order in the triangular lattice magnet TmMgGaO4. Nat. Commun.，2019，10：4530

 

[7] Chen B B，Chen L，Chen Z Y et al. Exponential Thermal Tensor Network Approach for Quantum Lattice Models. Physical Review X，2018 8：031082

 

[8] 孟子杨. 海森伯模型的谱，到底有多靠谱. 物理，2018，47(9)：595

 

[9] Hu Z，Ma Z，Liao Y D et al. Evidence of the Berezinskii-Kosterlitz-Thouless Phase in a Frustrated Magnet. Nature Communications，2020，11：5631

 

本文经授权转载自微信公众号“中国物理学会期刊网”。