阅读：0
听报道
你真的会解方程吗？今天我们从简单的解方程开始，为大家介绍一位英年早逝的数学家的工作，从这些工作中我们将看到优美的对称性，以及蕴含在其中的和谐奥妙。
撰文 | Marianne Freiberger
翻译 | Nothing
审校 | C&C
尼尔斯·亨里克·阿贝尔
1824年，一位年轻的挪威数学家尼尔斯·亨里克·阿贝尔取得了一个与某类方程相关的令人震惊的结果。不久之后，法国天才数学家埃瓦里斯特·伽罗瓦以深入的眼光证明了这一结果为什么是正确的——并在这个过程中开创了用数学研究对称性的先河。可惜两人都英年早逝，没有来得及享受他们的工作带来的好处。阿贝尔于1829年死于肺结核和贫困，时年26岁。伽罗瓦死于1832年，他在一场据称是为了争夺一个女人而进行的决斗中被杀死。当时他只有二十岁。
那么他们做出了什么样的工作？方程和对称性又有什么关系？
解方程
Solving Equations
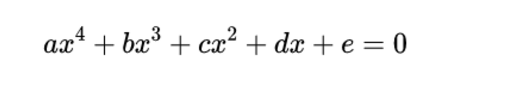
虽然关于二次，三次，四次方程的通解公式看起来有些复杂，但是它们只包含了有限个运算操作：加、减、乘、除、开平方、开三次方、开四次方。
很显然，你接下来会问，我们可以为五次方程找到一个类似的通解公式吗？
更一般的，包含x高阶项的多项式方程的通解公式长什么样子？
伽罗瓦画像 在他死后16年的1848年，由他的兄弟根据记忆所作
我们想要的是一个公式，这个公式只包含加减乘除和求根操作。如果一个方程具有这样一个通解公式，那么我们说这个方程是有根式解的。
1824年阿贝尔证明的结论是：对于一般的五次方程，不存在根式解。当然，这并不意味所有的五次方程都是没有根式解的。例如，多项式方程：
阿贝尔证明了这一结果，但几年后，伽罗瓦才真正意识到为什么五次方程不存在根式解。伽罗瓦常被认为群论的奠基人，群论是一门研究对称性的数学。 我们通常认为对称性是一种视觉现象：一幅画或图案可能是对称的。但是对称性和方程有什么关系呢？答案有些微妙，但非常美丽。
不变的对称性
Unchanging Symmetry
首先，让我们思考对称性真正的含义。我们说一个正方形是对称的是因为我们将它绕着中心轴旋转90度，或者将它对于各种轴做反射操作并不会改变它的外观。所以对称性意味着没有变化：如果我们对某个物体进行某种操作之后并没有改变它，那么它就具有对称性。
当我们思考二次方程式，我们可以发现少许对称性。例如，二次方程
方程具有两个离散的解，但是某种意义上，它们非常相似：只需在一个解上加上一个负号就可以得到另一个解。也许交换两个解并不会带来什么不同，就像对正方形做镜像操作一样意味着一种对称性一样，交换方程的两个解也许也意味着某种对称性。但究竟是哪种对称性呢？
加入无理数
Including Irrationals
蝴蝶有对称性，方程也有对称性！
交换两个解
Switching Solutions
伽罗瓦群
Galois's Group
为什么你解不出一般的五次方程？
Why you can't solve the general quintic?
纪念伽罗瓦的法国邮票
伽罗瓦所能证明的是，一个方程是否有根式解，取决于它的伽罗瓦群的结构。有时候伽罗瓦群可以被分成更小的分量，它们和取n次方根有关。如果是这种情况，那么方程拥有根式解。
然而，如果它无法以恰当的方式分被解成更小的分量，如果你不能把对称性分离出来，那么你就找不到一个只涉及加、减、乘、除和求根的通解，在这种情况下，方程不存在根式解。
我们可以证明，五次方程并不能以恰当的方式分解。因此，五次方程不存在根式通解。对于包含x的更高次幂的多项式方程也是一样的：它们没有根式通解。用群论研究方程的解被称为伽罗瓦理论，这一理论以其发明者的名字命名。
本文经授权转载自微信公众号“中科院物理所”。
原文链接：https://plus.maths.org/content/stubborn-equations
话题：
0
推荐
财新博客版权声明：财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有，未经博主及/或相关权利人单独授权，任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点，不代表财新网的立场和观点。
京公网安备 11010502034662号 