量子场论是目前我们描写微观世界的基本语言，描写所有基本粒子的标准模型就是用量子场论写出来的。但是量子场论有一个很严重的问题——它甚至还不是一个数学上自洽的理论。这是因为有相互作用的量子场论，目前是通过微扰级数展开来描述的。尴尬的是，这一级数展开根本就不收敛。在标准模型中，如果只取级数展开的前几项，标准模型会给出与实验非常接近的结果；但展开项越多，标准模型的结果就与实验差距越大，甚至会趋近于无穷大（参见《文小刚：标准模型还不是一个自洽的理论+温伯格演讲丨众妙之门》）。所以这样定义的量子场论并不自洽，也反映出我们对标准模型没有基本的理解。理论物理、数学物理的先驱一直想给量子场论一个更坚固的基础，找到一个非微扰的数学定义，是今天乃至后面几代数学家和物理学家有待解决的问题。

 

——文小刚

 

撰文 | Kevin Hartnett

 

编译 | 刘航

 

人们为理解量子场论中的数学而做出的加倍努力，将同时对数学和物理产生深远的影响。

 

在过去的一个世纪里，量子场论（Quantum Field Theory，QFT）已经被证明是有史以来最全面、最成功的物理学理论。它是一个涵盖了许多具体量子场理论的术语——就像“形状”的概念里面涵盖了正方形、圆形等具体图形。这些理论中最著名的被称为标准模型（Standard Model），正是这种物理学框架取得了如此的成功。

 

“它可以从根本上解释我们做过的每一个实验。”剑桥大学的物理学家大卫·汤（David Tong） 说。

 

然而，一个无可争辩的事实是，量子场论是不完整的。物理学家和数学家都不知道到底是什么让量子场论成为了量子场论。他们瞥见了全貌，却无法完全理解。

 

普林斯顿高等研究院的物理学家内森·塞伯格（Nathan Seiberg）表示：“各种迹象表明，我们可能有更好的方法来理解量子场论。正如管中窥豹，还看不到真正的全貌。”

 

数学，可能是使量子场论完整的语言；因为数学必须满足其内在的一致性，并且注重每一个细节。如果数学能够学会像描述完善的数学对象那样，同样严格地描述量子场论，那么一个更加完整的物理世界图景可能就会随之而来。

 

“如果你真的能以恰当的数学方式理解了量子场论，那么目前许多开放性的物理问题就有答案了，甚至可能包括引力的量子化。”普林斯顿高等研究院的主任罗伯特·戴克格拉夫（Robert Dijkgraaf）说道。

 

过去的几个世纪里，物理学中使用的所有其他数学思想都在数学中都有其天然的地位。但量子场论除外。

 

——内森·塞伯格，普林斯顿高等研究院教授

 

当然，这也不是一条单行道。千百年来，物理世界一直是数学发展的最伟大的灵感源泉。古希腊人发明了三角学来研究恒星的运动，而数学把它变成了一门有定义和规则的学科，今天的学生学习时不必了解其天文学起源。又过了近2000年，当牛顿想要理解开普勒的行星运动定律时，并试图找到一种严格的方式来思考无穷小的变化，这种冲动（以及莱布尼茨的启示）催生了微积分的诞生。然后数学把它拿了过去并改进——如今微积分已经无处不在。

 

现在，对于量子场论，数学家们想做同样的事情——将物理学家为研究基本粒子而发展的思想、对象和技术纳入数学的主体。这意味着我们要定义好量子场论的基本特征，这样未来数学家就不必考虑理论最初出现时的物理背景。

 

这样做的回报很可能是巨大的。当我们发现新的研究对象和新的结构，捕捉到数字、方程和形状之间某些最重要的关系时，数学就会发展。而这些都可以由量子场论来提供。

 

德克萨斯大学奥斯汀分校的数学家大卫·本-兹维（David Ben-Zvi）说，“物理学作为一种构造，本身是非常深刻的，而且往往会提供更好的方式让我们思考感兴趣的数学问题。物理学恰好是一种很好的形式。”

 

至少过去40年来，量子场论一直诱惑着有想法的数学家去探索其内涵。而近年来，他们终于开始理解量子场论本身的一些基本对象——将它们从粒子物理学的世界中抽象出来并转化为数学对象。

 

不过，目前数学家的努力还处于起步阶段。

 

“我们不能预见结果，但显然我期望我们目前看到的只是冰山一角。如果数学家真的弄清楚了量子场论，那么将给数学领域带来巨大的进步。”罗格斯大学物理学家格雷格·摩尔（Greg Moore）如是说。

 

永恒的场

 

人们通常认为宇宙是由基本粒子构成的，包括电子、夸克、光子等等，但物理学在很久以前就超越了这一观点。现在物理学家谈论的不再是粒子，而是粒子所对应的“量子场”，它们才是真实物理世界中的经纬线。

 

种类繁多的场布满了整个宇宙时空，像起伏的海洋一样波动。随着场产生涟漪并相互作用，粒子从场中出现，然后又在场中消失，就像转瞬即逝的波峰。

“粒子不是永远存在的实体。”汤说，“它是场的舞动。”

 

要理解量子场，最简单的方法就是从普通的场或者说经典场出发。比如，你想测量地球表面每一点的温度，那么你可以将无限多个要测量的点结合起来，形成一个包含了所有温度信息的几何对象，这个几何对象即为场。

 

一般来说，只要你有一些参量，它们可以在空间中以无限精细分解且唯一测量，场就会出现。加拿大滑铁卢圆周理论物理研究所的物理学家戴维·盖奥托（Davide Gaiotto）谈道，“在某种程度上，你可以对时空的每个点提出独立的问题，比如这里和那里的电场各是什么。”

 

当你观察量子现象时，量子场就出现了，比如时空中电子的能量。但量子场与经典场有本质的不同。

 

地球上某一点的温度是个经典的量，不管你是否测量，它就在那里。而对于电子的位置，只有在你观测的那一刻它们才有确定的位置。在此之前，它们的位置只能用概率来描述——量子场中的每个点被赋予概率值，以此来描述你在那里找到电子的可能性。在观测之前，你可以认为电子不在任何地方，也可以认为电子无处不在。

 

“物理学中的大多数事物不只是物体; 它们是存在于空间和时间中每个点的某种东西。”戴克格拉夫说。

 

量子场论提出了一系列被称为关联函数的方法，用来描述场中某一点观测量与另一点观测量之间的关联。

 

不同的量子场论会以特定的维度来描述物理。二维量子场论通常用于描述材料的行为，如绝缘体；六维量子场论与弦理论紧密相关；四维量子场论描述了我们实际四维宇宙中的物理，标准模型正是其中之一，也是最重要的量子场论。因为它是目前最适合描述宇宙的理论。

 

已知的12种基本粒子构成了我们的宇宙，每种粒子都对应于一个独特的量子场。在这12个粒子场的基础上，标准模型又增加了四个力场，代表了四种基本相互作用: 引力、电磁力、强核力和弱核力。标准模型将这16个场融合到一个方程中，描述了它们之间是如何相互作用的。通过这些相互作用，基本粒子被理解为它们各自量子场的涨落，这样，整个物理世界就呈现在我们眼前了。

 

这听起来可能很奇怪，但物理学家在上世纪30年代才意识到，物理学是基于场的，而不是粒子。他们用场的观点解决了一些最紧迫的矛盾：因果性以及粒子不会永远存在等问题。它还解释了物理世界中原本看似不可能的一致性问题。

 

“宇宙中所有相同类型的粒子都是一样的。”汤说，“如果我们用大型强子对撞机（Large Hadron Collider）制造一个新的质子，它与一个已经运动了100亿年的质子一模一样。这需要一些解释。”量子场论给出了这样的解释：所有的质子都是同一个基础质子场（或者更进一步，基础夸克场）中的波动。

 

但是，量子场论的解释能力是以极高深的数学为代价换来的。

 

汤表示，“量子场论是迄今为止数学中最复杂的对象，以至于数学家们尚不知如何理解它们。量子场论是数学家尚未发明的数学。”

无穷太多了

 

是什么让数学家觉得如此复杂呢？两个字：无穷。

 

当你在某一点观测量子场时，得出的结果并不是像坐标或温度那样的几个数字，而是一个矩阵——一组数字阵列。而且它还不是一个普通的矩阵，它无穷大，是一个有无穷多行和无穷多列的矩阵，也被称为算符。这也反映了量子场是如何覆盖了粒子从场中出现的所有可能性。

 

“一个粒子可以有无穷多个位置，这就必然要求描述位置和动量测量的矩阵也必须是无穷维的。”约克大学的卡西亚·雷兹纳（Kasia Rejzner）说。

 

当理论中出现无穷时，问题就来了：它与物理上的相关性作何解释？因为无穷是作为一种概念而存在，而不是任何实验可以测量的物理量。这也使其理论难以用数学方法来处理。

 

“我们并不喜欢一个描述无穷的理论框架。这就是为什么你开始意识到需要对此有更好的数学理解。”阿姆斯特丹大学的物理学家亚历杭德拉·卡斯特罗（Alejandra Castro）说道。

 

当物理学家开始思考两个量子场如何相互作用时，无穷大的问题变得更糟了。例如，在日内瓦郊外的大型强子对撞机上模拟粒子碰撞。在经典力学中，这类计算很容易：要模拟两个台球碰撞时会发生什么，只需指定每个球在碰撞点的动量即可。

 

现在换成两个量子场相互作用，你也会想做类似的事情：在它们相遇的时空点上，将一个场的无限维算符乘以另一个场的无限维算符。显然，这种计算——将两个无限维的对象在它们靠的无穷近时相乘——是很困难的。

 

“这就是发生严重错误的地方。”雷兹纳说。

 

了不起的成功

 

物理学家和数学家不能使用无穷大进行计算，但是他们已经发展了一些变通的应对之措——用近似的方法来回避这个问题。物理学家用近似的方法做出了一些预测，结果显示和实验非常吻合，毕竟实验也不是无限精确的。

 

“我们的实验测量可以精确到小数点后13位，理论近似的结果与实验测量惊人的一致。这是所有科学中最令人惊讶的事情。”汤说。

 

其中一种方法，是想象有一个无相互作用的量子场，即“自由”理论——不必担心有无穷维矩阵相乘的问题。因为这种情况下既没有运动，也没有碰撞，很容易用完整的数学细节来描述，只是这种描述没有太大价值。

 

雷兹纳认为，“这确实没什么意思，因为它描述的是一个孤立的场，没有任何互动。所以它仅仅是学术上的尝试。”

 

不过，你可以让它更有趣一些。物理学家在里面加入了一点相互作用，且试图用数学方法来控制相互作用的强弱，从而使理论适应不同的情况。

 

这种方法被称为微扰量子场论，表示在自由场中允许有微小的变化或扰动。你可以将微扰思想应用于类似自由理论的量子场论里，它对于验证实验也非常有用。“你会得到惊人的精确度，惊人的实验一致性。”雷兹纳说。

 

但如果相互作用不断增强，微扰的方法最终会失效。相互作用逐渐变大时，微扰论的结果变得越来越不精确，也就离真实的物理越来越远。这表明，虽然微扰论的方法对实验有一定指导意义，但它终究不能完全正确地描述整个宇宙——它在实际中有用，但在理论上是不坚实的。

 

“我们还不知道如何把所有的情况都考虑进来，也不知道怎么才能得出合理的结论。”盖奥托谈道。

 

我们一直将量子场论作为一种外部刺激，但如果它是一种内在刺激就好了。

 

——丹·弗里德，德克萨斯大学奥斯汀分校教授

 

另一种近似方案试图通过其他方式，渐渐靠近真实世界的量子场理论。理论上，量子场包含无穷精细的信息。为了构建这样的场，物理学家从网格或晶格出发，并将场定义在晶格线及彼此交叉的地方（费米子定义在格点上，规范场定义在链接上）。最初你只能在分立的格点上进行测量，而不能随意对量子场做连续的测量。

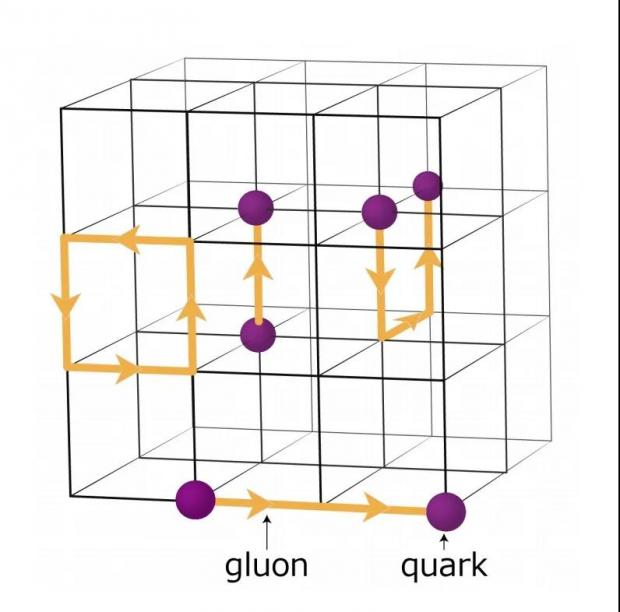
此后，物理学家不断提高格子的精细程度，使其精细程度的上限不断提高。随着格子变得越来越细密，可测量点的数目不断增加，越来越接近一个可以到处测量的场的理想概念。

 

“当点之间的距离变得非常小，这样就非常接近一个连续的场。”塞伯格说。用数学上的专业术语来说，他们所说的连续量子场其实是精细晶格的极限。

 

数学家们擅长处理极限，并且知道如何确定某些极限是否存在。例如，他们已经证明了无穷数列1/2+1/4+1/8+1/16…的极限是1。物理学家想要证明量子场是这种晶格过程的极限，只是目前他们还不知道该怎么做。

 

摩尔表示，“目前我们还不清楚如何计算这个极限，以及它在数学上意味着什么。”

 

物理学家并不怀疑不断精细的格点正朝着理想化量子场的概念发展。量子场论的预测和实验结果之间的高度吻合有力地说明了这一点。

 

赛博格说，“毫无疑问，这些极限是确实存在的，因为量子场论已经取得了极大的成功。”但是，有强有力的证据暗示某事是正确的，和最终证明它是正确的，完全是两码事。

 

量子场论渴望取代其他伟大的物理理论，而这种不精确正在拖量子场论的后腿。牛顿的运动定律、量子力学、爱因斯坦的狭义相对论和广义相对论——它们都只是量子场论想要讲述的更伟大故事的一部分。但与量子场论不同的是，它们都可以用精确的数学语言写下来。

 

“量子场论是作为一种描述所有物理现象的通用语言而出现的，但它在数学上却没有完善的定义。”戴克格拉夫谈道。对一些物理学家来说，这就是暂停脚步的原因。

 

戴克格拉夫说，“如果整个理论都依赖于某个核心概念，而这个概念本身并不能用数学的方式来理解，那你怎么能如此确信它能描述整个世界？这使整个问题更加尖锐。”

 

外部推动

 

即使在这种不完整的状态下，量子场论也促成了许多重要的数学发现。两者的交互通常是这种模式：物理学家使用量子场论进行计算时，偶然发现了令人惊讶的结果，然后数学家试图对其进行解释。

 

“这（量子场论）就是一台创意机器。”汤说。

 

在一个基本层面上，物理现象与几何有着密切的关系。举个简单的例子，如果你让一个小球在一个光滑的表面上运动，它的轨迹就是沿着任意两点之间的最短路径，也就是所谓的测地线。用这种方式，物理现象可以探测出一个形状的几何特征。

 

现在，我们把小球换成一个电子。电子以概率的形式可以存在于表面上任意一点。通过研究那些概率所对应的量子场，你可以了解这块表面的总体性质（数学家称之为流形），比如它有多少个洞。这是研究几何学和相关拓扑学领域的数学家想要回答的一个基本问题。

“即便一个粒子即使呆在原地不动，我们也会知道流形的拓扑结构。”汤说。

 

上世纪70年代后期，物理学家和数学家开始应用这种观点来解决几何中的基本问题。到90年代初，塞伯格和他的合作者爱德华·威滕（Edward Witten）提出了如何用这种思想来创造一种新的数学工具——Seiberg-Witten不变量——将量子现象转化为一个指数，其反映了形状的纯数学特征: 通过计算量子粒子以某种方式出现的次数，你就能有效地计算出一个形状中洞的数量。

 

“威滕表明了量子场论能给几何问题提供完全意想不到却又极其精确的洞见，使棘手的问题变得可解。”牛津大学的数学家雷姆·西格尔（Graeme Segal）表示。

 

另一个数学与物理相互融通的例子也发生在20世纪90年代初，当时物理学家正在进行与弦理论有关的计算。他们根据完全不同的数学规则在两个不同的几何空间中进行运算，结果总是得出一长串却彼此完全匹配的数字。数学家们从这个线索出发，仔细研究后发展出一个全新的研究领域——镜像对称。数学家研究出它们为何如此吻合，还发现了许多类似的现象。

 

“物理学会提出这些惊人的预测，数学家则会尝试用自己的方法来证明它们。”本-兹维说，“这些预测既奇怪又奇妙，可是结果证明，它们几乎总是正确的。”

 

尽管量子场论成功地为数学创造了可寻的线索，但其核心思想仍然几乎完全存在于数学之外。与多项式、群、流形等其他起源于物理学并且如今已被熟练应用的方法相比，量子场论仍然没有被数学家们理解得足够好。

 

对物理学家来说，这种与数学的疏远关系表明，对于量子场论，还有很多东西需要深入理解。塞伯格说：“过去的几个世纪里，物理学中使用的所有其他数学思想都在数学中都有其天然的地位。但量子场论除外。”

 

我想说，物理学家不一定洞悉一切，但物理学可以。

 

——大卫·本-兹维，德克萨斯大学奥斯汀分校教授

 

而对于数学家来说，似乎量子场论和数学之间的关系应该比偶尔的互动更为深刻。这是因为量子场论包含了许多对称或基本结构，这些结构决定了场中不同部分的点如何相互关联。这些对称性具有物理意义——它们体现了诸如能量等守恒量是如何随着量子场的演化仍保持守恒的。另一方面，在数学上它们本身也是很有趣的研究对象。

 

卡斯特罗表示，“数学家可能关心某种对称性，我们可以把它放在物理背景中。如此一来，两个领域之间就搭起了一座美丽的桥梁。”

 

从不同类型方程的解到素数分布，数学家几乎对所有问题都使用了对称性和几何学来研究。通常，几何编织出了数字问题的答案。而量子场论为数学家们提供了全新的且丰富多彩的几何对象——如果数学家能直接运用它，也许他们能做的超乎想象。

 

“从某种角度上来说，我们只是在摆弄量子场论。”德克萨斯大学奥斯汀分校的数学家丹·弗里德（Dan Freed）说，“我们一直将量子场论作为一种外部刺激，但如果它是一种内在刺激就好了。”

 

为量子场论铺路

 

数学不会轻易接纳新的对象。许多基本概念都是经过了长时间的检验，才在数学领域中找到了正确且严格规范的位置。

 

比如实数——表示数轴上无穷多个刻度的全部。这一概念在数学上实际使用了近2000年，数学家才在定义它的方式上达成一致。终于在19世纪50年代，数学家们确定了一个精确的陈述，只用三个词语表达，即“完备、有序、域（complete ordered field）”。它们是完备的，因为实数没有任何间隙；它们是有序的，因为总有一种方法来确定一个实数是否大于或小于另一个实数；它们形成了一个“域”，这对数学家来说意味着它们遵循算术规则。“从历史上看，这三个词来之不易。”弗里德说。

 

为了使量子场论变成内在刺激——成为一种数学家可以为自己研究所使用的工具——数学家想对量子场论进行与他们对实数相同的处理：找出一个清晰的特征列表，任何特定的量子场论都需要满足里面的要求。

爱尔兰数学家凯文·科斯特洛

 

加拿大圆周研究所的数学家凯文·科斯特洛（Kevin Costello）做了大量关于将量子场论转化到数学上的工作。2016年，他与人合著了一本教科书（Factorization Algebras in Quantum Field Theory: Volume 1），他们将微扰量子场论建立在坚实的数学基础上，包括如何形式化地处理随着相互作用增加而出现的无穷量。这是继早期2000年代的代数量子场论后的又一尝试，代数量子场论也寻求类似的目标，雷兹纳在他也是于2016年出版的书（Perturbative Algebraic Quantum Field Theory）中回顾了这项研究。虽然现在的微扰量子场论仍然不能真正描述宇宙，但数学家们知道如何处理它产生的物理上无意义的无穷大。

 

摩尔表示，“科斯特洛的贡献是非常巧妙和有见地的。他把（微扰）理论置于一个适用于严格数学的漂亮的新框架中。”

 

科斯特洛解释说，他写这本书的目的是想让微扰量子场论更加连贯。“我发现有些物理学家使用的方法是不可论证的，而且只针对特定的情形。我想要使其理论更自洽，让数学家可以更好地研究它。”

 

通过准确地说明微扰理论的工作原理，科斯特洛创造了一个基础理论框架。在此基础上，物理学家和数学家可以构建满足要求的新量子场论。这个理论很快就被该领域学者所接受。

 

“一定会有许多年轻人尝试这个框架。他的书已经产生了极大的影响。”弗里德说。

 

科斯特洛也一直致力于定义什么是量子场论。在简化形式下，量子场论需要一个几何空间，在这个空间中你可以对每一点进行观测，并结合关联函数来描述不同点间的观测量如何相互关联。科斯特洛的工作描述了一组关联函数需要具备的性质，以便为量子场论提供一个可行的基础。

 

我们最熟悉的量子场论，比如标准模型，可能包含了一些不是所有量子场论都具备的额外特征。没有这些特征的量子场论可能描述了其他尚未被发现的特性，而这些特性可以帮助物理学家解释标准模型无法解释的物理现象。如果你对量子场论的想法只停留在我们已知的版本，你甚至很难想象其他必要的可能性。

 

盖奥托比喻道：“在一个巨大的灯柱下，你可以找到场的理论，比如标准模型，而在它周围是一大片量子场论的黑暗区域。我们不知道它如何定义，但我们确定它就在那里。”

 

科斯特洛用他对量子场的定义照亮了其中一部分黑暗空间。从这些定义出发，他发现了两个令人惊讶的新型量子场理论。虽然它们都不是描述我们的四维宇宙的，但它们确实都满足几何空间里关联函数的核心要求。这是纯粹的思想结果，类似于你在物质世界中发现了一类全新的形状，一旦你对它们有了一般定义，你就可以思考与实物毫无关系的例子。

 

如果数学可以确定量子场论的全部可能性，而且是满足一般定义（包含关联函数）的所有不同的可能性，物理学家就可以从中找到那个能解释他们最为关心的物理问题的具体理论。

 

“我想知道全部量子场论的空间，因为我想知道量子引力是什么。” 卡斯特罗说道。

 

接力挑战

 

显然，努力刚刚开始。迄今为止，所有用完整数学描述的量子场论都依赖于各种简化，这使得它们在数学上更容易处理。

 

研究更简单的二维量子场论代替四维量子场论，是简化问题的一种方法，这项工作可以追溯到几十年前。最近，法国的一个研究小组确定了这个著名的二维量子场论的所有数学细节。

 

有一些简化方法是假设量子场是对称的，可是这不符合物理现实。但从数学的角度，这使它们更容易处理，例如“超对称”量子场论和“拓扑”量子场论。

 

接下来，也是更困难的一步，就是移除“拐杖”——为物理学家最想描述的真实物理世界的量子场论提供完整的数学描述：一个四维连续的宇宙，在这个宇宙中，所有相互作用都可能同时发生。

 

“比较尴尬的是，我们没有一个四维时空的非微扰量子场论。”雷兹纳谈道，“这是个难题，显然需要一两代数学家和物理学家才能解决。”

 

但这并不妨碍数学家和物理学家的渴求。对于数学家来说，量子场论是他们所希望研究的那类最为丰富的对象。要定义量子场论所共有的特性，几乎肯定需要合并数学的两大支柱——分析和几何。前者来解释如何控制无穷大；后者则提供讨论对称性的语言。

 

“就数学本身而言，这是一个令人着迷的问题，因为它结合了两个伟大的思想。”戴克格拉夫说。

 

如果某天数学家们能够理解量子场论了，那么与其相关的数学发现将是不可估量的。很久以前，数学家定义的一些对象的特征属性，比如流形和群，现在几乎渗透到数学的每个角落。当它们最初被定义时，数学家是不可能预见所有成果的。量子场论也是如此。

 

“我想说，物理学家不一定洞悉一切，但物理学可以。”本-兹维说，“如果你提出了正确的问题，那可能已经有数学家在寻找答案了。”

 

对于物理学家来说，量子场论的完整数学描述也是他们领域最重要目标的另一面——对物理现实的完整描述。

 

塞伯格说：“我觉得有一种知识结构可以涵盖所有这些，也许它将涵盖所有的物理。”

 

现在就等数学家们把它挖掘出来。

 

参考资料

 

[1] 原文链接：https://www.quantamagazine.org/the-mystery-at-the-heart-of-physics-that-only-math-can-solve-20210610/

 

[2] https://indico.cern.ch/event/696311/contributions/3204292/attachments/1755653/2846405/cichy-cracow2018.pdf