统计力学通过概率分布来联系系统的微观状态和宏观性质。几个世纪以来，统计力学中相互矛盾的描述一直困扰着物理学家，使他们一度为热力学的三个妖精所困：洛施密特妖可以让不可逆的热力学从时间可逆的微观动力学中产生吗？麦克斯韦妖可以打破热力学第二定律吗？隐藏在概率背后的无知是一种固有存在，还是有一个拉普拉斯妖，它对宇宙中每个分子的微观状态都无所不知？将量子力学引入统计力学，帮助我们永久地驱除这三个妖精。

撰文 | Katie Robertson

翻译 | 潘佳栋

审校 | 张澳、梁金

热力学是一个奇怪的理论。它虽然是我们理解世界的基础，但与其他物理理论有很大的不同。出于这个原因，它被称为物理学的“乡村女巫”（village witch）文[1]。热力学的奇怪体现在经典统计力学的哲学含义上。早在相对论和量子力学将现代物理学的悖论带入公众视野之前，路德维希·玻尔兹曼（Ludwig Boltzmann）、詹姆斯·克拉克·麦克斯韦（James Clerk Maxwell）和其他统计力学的先驱就在与几个可能破坏热力学的思想实验（妖精）搏斗。 尽管作出了巨大的努力，麦克斯韦和玻尔兹曼仍无法完全战胜困扰“乡村女巫”的妖精，这主要是因为热力学仅限于经典视角。如今，量子实验和理论发展使研究人员和哲学家对热力学和统计力学有了更深入的了解。量子理论使我们能够通过“量子驱魔”（quantum exorcism），一劳永逸地解决困扰热力学的妖精。 

图1. 这幅版画描绘了一个将头伸出宇宙边缘的人，常被用来象征人类对科学知识的追求。| 来源：Engraving from Camille Flammarion, L’atmosphère: météorologie populaire, 1888, p. 163/public domain.

1. 洛施密特妖和时间可逆性

玻尔兹曼是统计力学和热力学的创始人，他对热力学领域的一个看似悖论的问题非常着迷。一个达到热力学平衡的系统所表现出的不可逆行为，如一杯咖啡的冷却或气体的扩散，是如何从更基本的时间可逆的经典力学中产生的？[2] 这种平衡行为在时间上仅单向发生。如果你看到一个酒杯打碎的视频，你能立即判断视频是否在倒放。相比之下，更基础的经典和量子力学是时间可逆的。如果你看到一个很多台球碰撞的视频，你不一定能知道视频是否在倒放。玻尔兹曼在整个职业生涯中进行了一系列尝试，从基本的可逆动力学出发，解释不可逆的热力学平衡行为。 玻尔兹曼的朋友约瑟夫·洛施密特（Josef Loschmidt）对这些尝试提出了著名的反对意见。他认为，基础的经典力学允许出现动量反转的可能性，从而回溯系统并使其“反平衡”到早期的低熵状态。玻尔兹曼向洛施密特提出挑战，要求他尝试逆转动量，但洛施密特无法做到这一点。尽管如此，我们可以设想一个可以做到这一点的妖精——洛施密特妖（Loschmidt’s demon）。毕竟，将手伸进一箱气体并扭转每个分子的轨迹只是现实实现上不可能，而不是物理上不可能。 自1895年洛施密特去世以来，技术的发展扩大了现实世界可实现的范围（见图1）。厄温·哈恩（Erwin Hahn）在1950年的自旋回波（spin-echo）实验中实现了洛施密特关于逆转动量的设想，这在洛施密特生前看来是不可能的。在该实验中，厄温·哈恩通过一个射频脉冲将已经变得无序的原子自旋带回早期状态。如果现实中有可能逆转动量，这对热力学平衡意味着什么？洛施密特妖胜利了吗？ 

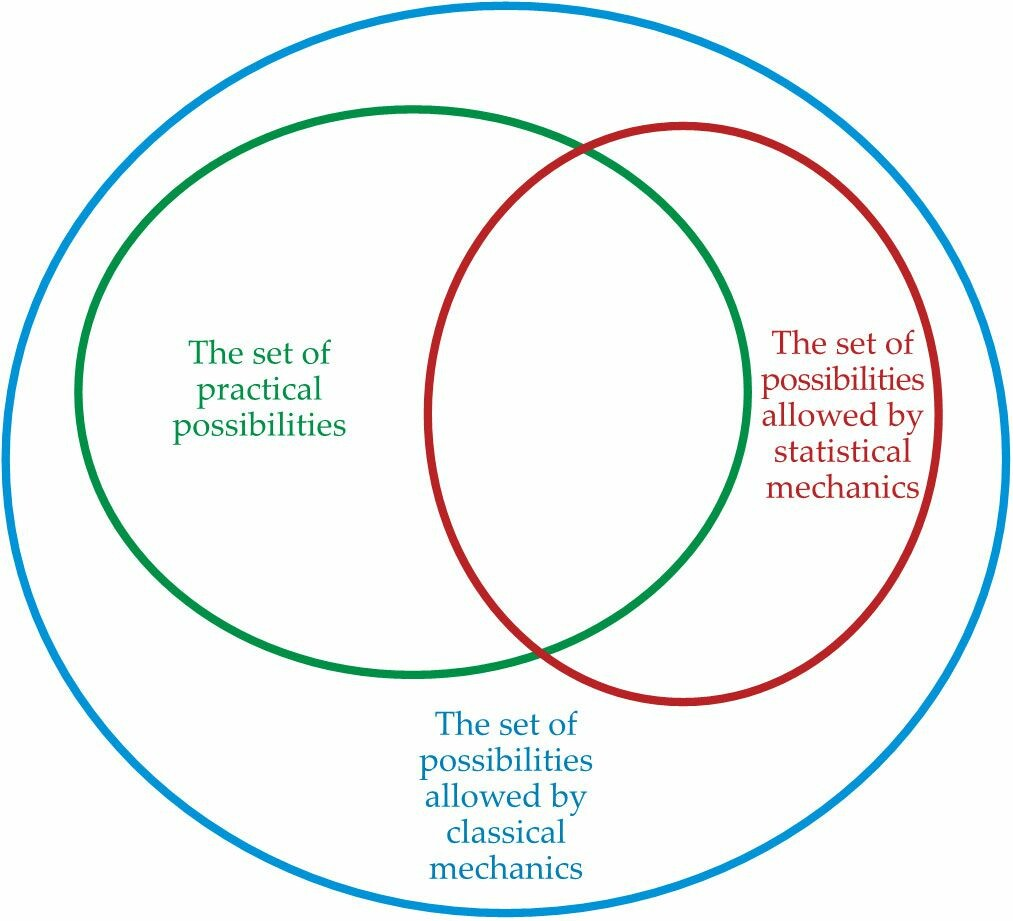
图2.可以用相交的椭圆来描述各种物理理论允许的可能性集合。经典力学所允许的可能性集合（蓝色椭圆）既包含统计力学所允许的可能性集合（红色椭圆），也包含现实中可以实现的可能性集合（绿色椭圆）。洛施密特妖在经典力学下是可能存在的，因为该范式存在系统动量被逆转的可能性。然而，统计力学下，系统平均而言不能减少熵，这就排除了任何妖精存在的可能性。尽管玻尔兹曼认为，逆转动量的妖精实际上是不可能存在的，但自旋回波实验已经证明，妖精在极少数情况下可以存在。因此，洛施密特妖在蓝色和绿色的椭圆内，但不在红色的椭圆内。

  与我们将遇到的其他两个妖精（麦克斯韦妖与拉普拉斯妖）不同，洛施密特妖可以与现实世界和平相处。然而，事实证明自旋回波实验是一个特例。现实世界中，大多数系统都趋向平衡状态，而不是回溯到非平衡状态。但洛施密特妖生动地提醒我们，力学的基本定律允许一个系统回溯到原来的状态。为什么我们在现实世界中没有看到这种可能性的发生？为什么气体不会被压缩到更小的体积？为什么鸡蛋不会从破碎状态恢复，一杯咖啡不会自发升温？ 答案在于规律和初始条件的区别。考虑将石头扔进池塘，其初始条件为石头击中池塘，这解释了为什么我们看到水波向外扩散。相比之下，我们从来没有看到水波向内汇聚，把石头从池塘深处推出来，因为该过程所需的初始条件是非常难以设置的。同样地，在涉及气体的系统中，典型的初始条件解释了为什么它们会趋向平衡状态。但是，确实也存在具备精确相关性的特殊初始条件，可能会导致系统达到反平衡的情况，例如咖啡自发地变热或石头被推出池塘。换句话说，根据物理学的微观动力学定律，反平衡是可能出现的，但这只有当系统具有非常特殊的初始条件时才有可能。   

2. 麦克斯韦妖与热力学第二定律

到目前为止，物理学中最著名的假想妖精是麦克斯韦在1867年设想的妖精（见图2）。他设想了在充满气体的盒子里存在一个妖精，它可以观察单个气体分子。盒子中间有一个隔板，如果这个妖精看到一个快速移动的气体分子，它就打开隔板上的活动门，让快速移动的分子通过，而把慢速移动的分子留在隔板的另一边。反复这样操作会使隔板两边产生温度差，而热机可以利用这个温差来做功，这与热力学第二定律相矛盾。 

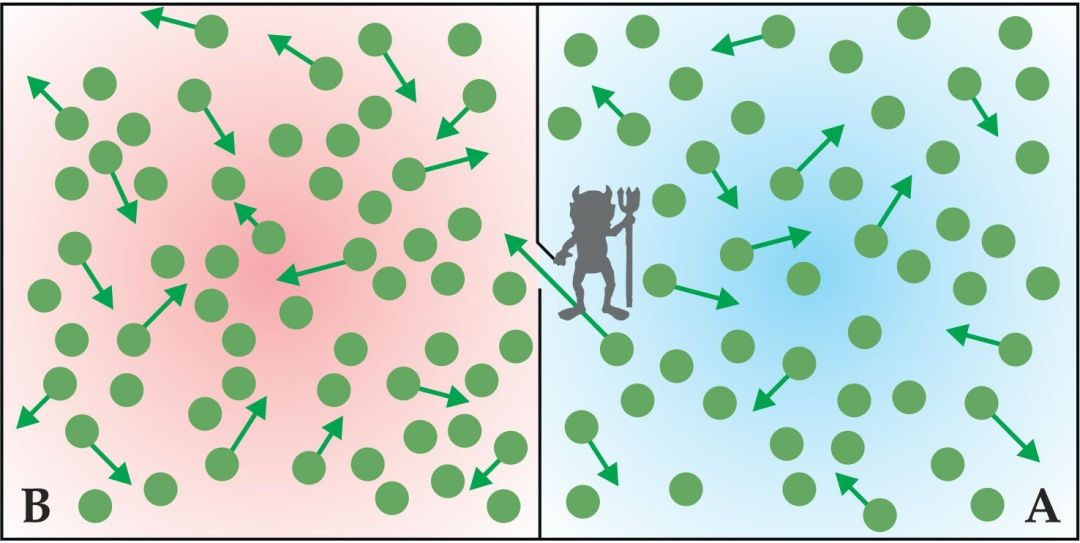
图3. 麦克斯韦妖是一个假想的生物，它可以观察一个充满气体的盒子里的各个分子，盒子中间有一个隔板将A室和B室分开。如果这个妖精看到一个快速移动的气体分子，它就打开隔板上的活动门，让快速移动的分子进入B室，而把慢速移动的分子留在A室。麦克斯韦妖反复这样操作将在隔板的两边建立起温度差。而热机可以利用这个温差来做功，这与热力学第二定律相矛盾。

 麦克斯韦妖和洛施密特妖属于同类问题吗？即麦克斯韦妖是否仅在现实中难以实现，而不是物理上的不可能情况？麦克斯韦认为两者是同类问题。根据物理哲学家韦恩·米尔沃德（Wayne Myrvold）的说法，麦克斯韦认为，“只是我们目前（也许仅是暂时）无法操纵单个分子......才会阻止我们做这个小妖精能做的事。”[3] 在150多年前时，操纵单个分子的可能性可能看起来很小，但今天情况已不再如此。从特制的实验装置到自然界中发现的分子机器，类似麦克斯韦妖的装置比比皆是。例如，使用棘轮式机构（ratchet-style mechanisms）的生物分子机器[4]，类似于理查德·费曼（Richard Feynman）在1962年的一次演讲中所提出的麦克斯韦妖。 此外，研究人员似乎已经能够在实验中实现麦克斯韦妖。东京一个由佐野正明（Masaki Sano）领导的小组，在2010年设计了一个麦克斯韦妖式的实验。通过使用一个倾斜的光学晶格来操纵单个粒子，他们创造了一个“螺旋楼梯”。平均而言，粒子倾向于“下楼”。通过使用CCD相机，实验人员实时监测粒子位置的波动。当粒子“上楼”时，他们改变电压并将其困在较高的位置，就像妖精关闭了活动门一样（见图3）。通过重复这一过程，他们能够逐渐将粒子向上移动并做功。 

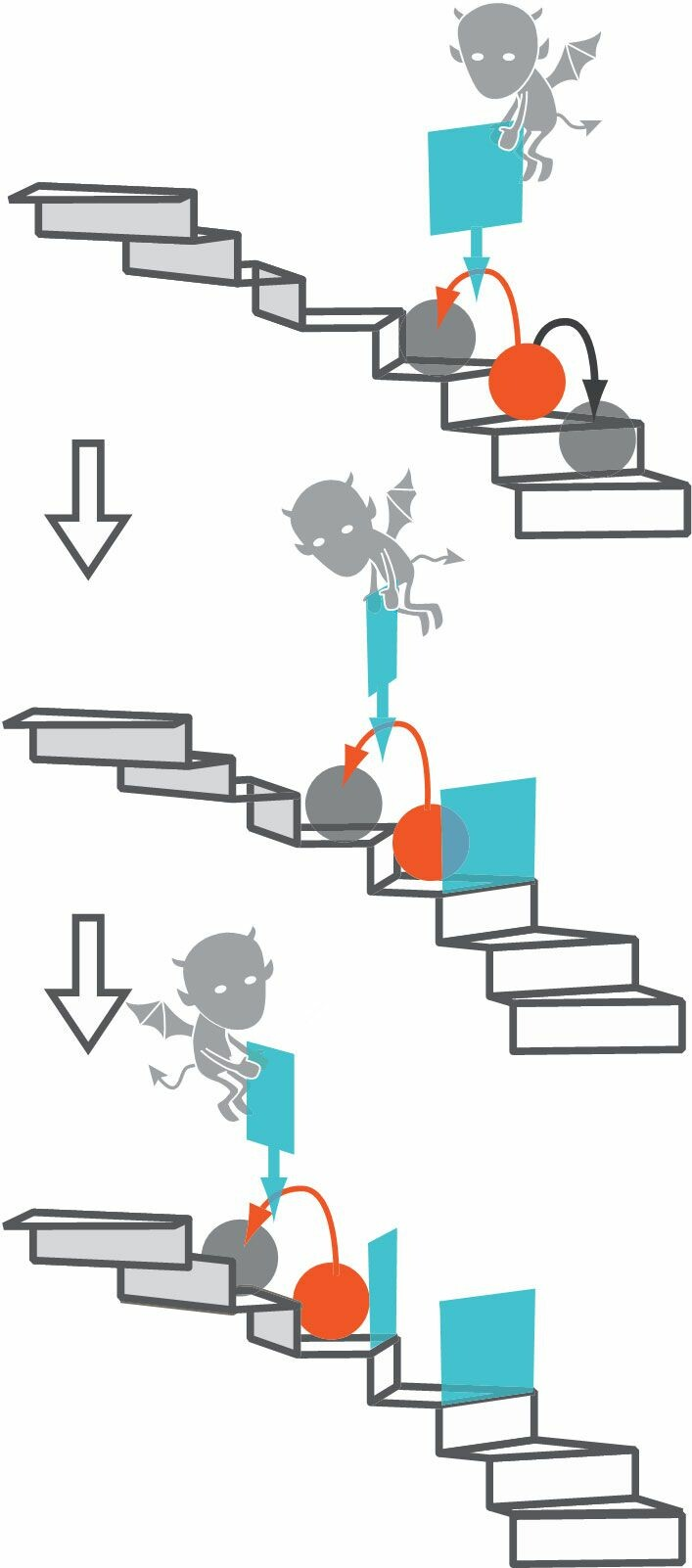
图4. 佐野正明的小组在2010年设计了一个麦克斯韦妖式的实验。他们使用倾斜的光学晶格来创造“螺旋楼梯”，使粒子倾向于“下楼”。实验人员实时监测粒子位置的波动，当粒子“上楼”时，他们改变电压并将其困在较高的位置，正如麦克斯韦妖关闭活动门。| 来源：Adapted from S. Toyabe et al., Nat. Phys. 6, 988, 2010, doi:10.1038/nphys1821.

 这种巧妙的装置是真正的麦克斯韦妖吗？它会使热力学第二定律失效吗？尽管它们的机制似乎与麦克斯韦妖类似，但仍有必要仔细计算熵。只有当过程中整个系统的熵减小时，该过程才违反了热力学第二定律。可以举一个熟悉的例子，理想气体的熵在等温压缩过程中减小了，但环境中的熵增意味着系统的总熵增加。那么这一装置的环境中是否存在补偿性的熵增，从而否定了违反热力学第二定律的可能性？ 麦克斯韦妖一直以来备受争议[5]。许多物理学家认为，麦克斯韦妖的活动会产生熵值成本（entropic cost），因为这些巧妙的装置会导致系统其它地方的熵增加，所以麦克斯韦妖没有真正违反第二定律，但仍有一些物理学和哲学家不同意这个观点[6]。熵值成本源于麦克斯韦妖的活动。麦克斯韦妖需要进行反馈的操作：如果分子移动得快，它就会打开活动门，如果分子移动得慢，它就会关闭活动门。 这就要求麦克斯韦妖具有记忆，该记忆必须在循环过程结束时重置。但是重置记忆会产生熵值成本，这可以通过罗尔夫·兰道尔（Rolf Landauer）在1961年提出的理论来量化。他指出，每重置一个信息位，熵就会增加kBln2（kB是玻尔兹曼常数）。换句话说，擦除信息将付出熵的代价。兰道尔原理在热力学和信息论之间建立了联系——尽管它们之间的确切关系仍有争议。 尽管如此，在我看来，兰道尔原理解释了为什么无论如今的实验者多么聪明，手指多么灵活，都不能制造出真正违反热力学第二定律的热机，以解决全球能源危机。一旦窥探到其幕后的原理，我们就会发现，今天所谓的麦克斯韦妖是灵巧的幻术师而不是真正的魔术师。 当代热力学的许多活动来自于量子信息论与热力学的结合。量子信息论能把麦克斯韦妖从兰道尔原理的桎梏中释放出来吗？遗憾的是，它不能。热力学第二定律适用于所有具有相空间体积的动力学形式，而经典力学和量子力学都符合这一标准。此外，量子操作甚至可能有额外的熵值成本，因此量子计算机不能达到兰道尔极限（Landauer limit）[7]。   

3. 量子蒸汽朋克

麦克斯韦对热力学和统计力学性质的哲学推测超越了他提出的麦克斯韦妖。为了使这些概率理论与他的古典世界观相协调，麦克斯韦提出了两个哲学主张。第一，热力学只适用于具有许多自由度的系统；第二，热力学是以人类为中心的，并取决于我们人类的观点。这些哲学假设在今天还能成立吗？ 自20世纪中期以来，热力学的实验和理论发展表明，麦克斯韦的第一个主张是不正确的。在麦克斯韦的时代，热力学的产物是为工业革命提供动力的蒸汽机。但今天的热力学革命——尼科尔·永格·哈尔彭（Nicole Yunger Halpern）称之为“量子蒸汽朋克”（Quantum steampunk）的子领域——是在原子尺度上的。[8]例如，德里克·斯科维尔（Derrick Scovil）和埃里希·舒尔茨·杜波依斯（Erich Schulz-DuBois）在1959年首次提出量子热机，证明了三层微波散射器如何作为热机发挥作用。随着量子信息论的出现，这些微小的热力学系统现在为整个子领域提供了发展空间。[9]其他类型的量子热机使用多能级原子、量子比特和量子点等微观系统作为热机的工质。 量子热机和经典热机有什么不同？在量子体系中热机可以获得额外的资源，纠缠和相干性可以作为“燃料”使用。尽管如此，仍然没有人找到绕过热力学第二定律的方法。[10]也许这是意料之中的，毕竟，赛斯·劳埃德（Seth Lloyd）认为，“除了死亡、税收和热力学第二定律，生活中没有什么是永恒的”。 然而，这两种类型的热机有所不同。在经典热力学中，只有当热力学过程准静态进行，或无限缓慢地进行时，才能达到最大的卡诺效率，但这意味着热机产生的功率趋于零。这一限制导致了有限时间热力学（finite-time thermodynamics）的发展，而在这一框架内，还有其他对热机效率限制的因素。在有限时间内，量子热机可以比经典热机更有效率，但两者仍然都受到卡诺极限的限制。[11] 如果热力学不局限于宏观的大系统，那么它是普遍成立的吗？许多物理学家认为，它是普遍成立的。阿尔伯特·爱因斯坦（Albert Einstein）曾经说过，“它是唯一具有普适性的物理理论，我相信在其基本概念的适用范围内，它永远不会被推翻。”[12]如今，热力学被用来理解各种概念，如量子热机、球状星团、黑洞、细菌群，以及更有争议的大脑。[13]    

4. 热力学是以人类为中心的吗？

麦克斯韦的第二个哲学主张是什么，即热力学是我们对现实看法的一个特征？正如他在1877年《大英百科全书》的一篇文章中写道，“区分热力学中有序运动和无序运动的不是物质本身的属性，而是感知它们的思想。”[14]事实证明，麦克斯韦的观点具有持续的影响力。例如，珀西·布里奇曼（Percy Bridgman）附和麦克斯韦的观点，他在1941年断言：“热力学比物理学的其他分支更有人类起源的味道——观察者通常出现在争论中。”[15] 为什么会这样呢？我们以蜜蜂为例。昆虫看到的花园与我们非常不同，因为它们的眼睛对电磁频谱的其他波段敏感。热力学是人类中心主义的说法，或者说是依赖于观察者的说法，意味着如果我们是不同类型的生物，热力学特征（如熵）可能看起来是不同的，或者根本就不存在。在这种观点下，热力学将类似于一副玫瑰色的眼镜，我们通过它来理解和感知世界，但却看不到它的实际面貌。 这样一来，麦克斯韦的想法就把热力学与人联系在一起。考虑到量子力学已经让许多人接受观察者似乎无法从物理学中消除的情况，热力学也依赖于观察者的观点可能看起来并不奇怪。但麦克斯韦并不是在向像蜜蜂一样的一般观察者发出呼吁。他认为，热力学是专门以人类为中心的。正如他在《大英百科全书》的同一篇文章中写道：“处于中间阶段的人类可以掌握部分形式的能量，只有对人类而言，能量似乎不可避免地从可用状态转为耗散状态。”[16]理解这种人类中心主义充满了挑战。例如，不管我们对咖啡的了解如何，也不管我们对现实的看法如何，杯中的咖啡都会降温，这似乎不可否认。 我们对人类中心主义存在的担心程度完全取决于对科学事业本身的立场。科学家是否真的在以独立于人类视角的方式，研究现实的深刻本质？还是说科学仅仅是一个工具和手段，要求我们“闭嘴并计算（shut up and calculate）”。关于科学现实主义的辩论，已经延续了几个世纪而没有定论，但最近量子热力学的发展为那些想摆脱热力学中人类中心观点的人提供了一些希望。   

5. 驱除拉普拉斯妖，摆脱无知

经典统计力学的基本假设之一是系统微观态的等几率假设。但是我们应该如何理解统计力学中的概率呢？多年来，这个问题受到了玻尔兹曼、保罗·埃伦费斯特（Paul Ehrenfest）和塔蒂亚娜·埃伦费斯特·阿法纳西娃（Tatiana Ehrenfest-Afanasyeva）等人的关注。在此，我们将注意力集中在由物理学家埃德温·杰恩斯（Edwin Jaynes）推广的主流观点，该观点认为统计力学的基本假设源于我们对微观态细节的无知。因为杰恩斯的观点强调我们人类的无知，它暗中强化了热力学是以人类为中心的观点。我们必须假设每个微观状态出现的可能性相等，因为我们不知道系统处于哪个确切的微观态。 在这里，我们遇到了我们的第三个也是最后一个哲学妖精：皮埃尔·西蒙·拉普拉斯（Pierre Simon Laplace）于 1814 年首次提出的拉普拉斯妖（见图4）。拉普拉斯妖是一个假想的观察者，它知道宇宙中每个分子的位置和动量。换句话说，它知道宇宙中每个系统的确切微观状态。 

图5. 拉普拉斯妖是一个假想的观察者，知道宇宙中每个分子的位置和动量。| 来源：Ele Willoughby, linocut, 2011.

 在统计力学中，系统的熵通常用吉布斯公式表示，SG=∫ρlnρdNqdNp，其中 ρ(q,p) 表示N个粒子的位置和动量相空间 {q1, …, qN; p1, …, pN} 上的概率分布（例如微正则分布）。但是对于拉普拉斯妖，ρ=1，因为它知道系统确切的微观状态。无所不知意味着拉普拉斯妖会计算出系统的吉布斯熵为零。因此，杰恩斯的统计力学概率观点有一个根本性的结论：人类分配给吉布斯熵的值取决于人类对世界的了解。 拉普拉斯妖是否威胁到杰恩斯的统计力学观点？不完全是。幸运的是，人们可以通过转向统计力学的量子观点来驱除拉普拉斯妖。在经典统计力学中，概率是添加到系统的微观动力学中的一个额外成分。根据杰恩斯的观点，由于我们的无知，这是一个必要的步骤。但在量子情形下，概率已经是理论的固有部分，所以没有必要把无知加入到描述中。换句话说，统计力学和量子力学的概率是一样的。 但在量子力学中，玻恩定则（Born rule）意味着一个量子态编码了不同测量结果的概率。这些概率如何能产生统计力学中熟悉的概率分布？这个问题特别棘手，因为量子力学给一个孤立的系统分配了一个明确的状态，称为纯态（pure state）。与此相反，统计力学给这样一个系统分配了一个固有的不确定状态，称为最大混合态（maximally mixed state），其中每种状态出现的可能性都是相等的。从表面上看，统计力学和量子力学似乎有冲突。 独特的量子纠缠（entanglement）性质是解决这一冲突的关键[17]（见图5）。考虑一个与周围的热浴纠缠在一起的量子比特（qubit）。因为它们是纠缠在一起的，如果这两个系统中的一个被单独拿出来，它将处于一种被称为混合态的内在不确定状态。然而，由量子比特和热浴组成的复合系统处于纯态，因为作为一个整体时，该复杂系统是孤立的。假设周围的环境足够大，那么对于复合系统所处的几乎任何纯态，量子比特将处于一个非常接近于经典统计力学所指定的状态。 

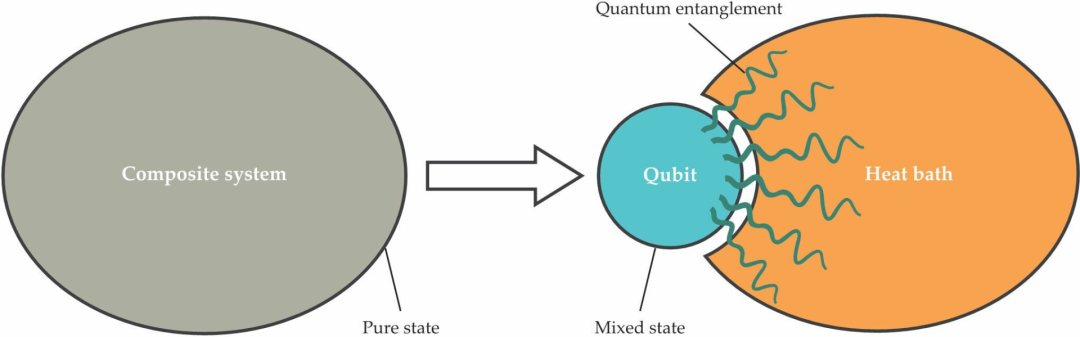
图6. 量子纠缠解释了拉普拉斯妖被消灭的原因。考虑一个纠缠在一起的量子比特和一个热浴（左图）。如果把量子比特单独拿出来，它将处于一种混合态，热浴也是如此。但是，由量子比特和热浴组成的复合系统（右图）处于纯态，因为它作为一个整体是孤立的。假设环境足够大，对于复合系统所处的几乎任何纯态，量子比特将处于非常接近于经典统计力学所赋予它的状态。因此，该系统表现出的行为会使人认为统计力学的基本假设是真的。统计力学分配的概率分布与量子状态是不可区分的，这意味着统计力学不需要杰恩斯引入的“无知”。因此，拉普拉斯妖被打败了。| 来源：Adapted from S. Deffner, Nat. Phys. 11, 383, 2015, doi:10.1038/nphys3318. 

换句话说，被研究的量子比特系统的行为就好像复合系统处于最大混合态，即好像复合系统的每个微观状态的可能性相同。概率的本质最终是量子的，但系统的行为会使人认为统计力学的基本假设是真的。因此，量子描述的概率分布与统计力学中的概率分布没有区别。 这个结论是如何战胜拉普拉斯妖的？量子力学给事件赋予概率，不是因为我们不知道它们的准确值，而是因为我们和拉普拉斯妖都无法知道准确值。概率是量子力学内在的一部分。当描述自身纠缠系统的时候，拉普拉斯妖不可能比我们知道更多信息。 阿瑟·爱丁顿（Arthur Eddington）在1928年宣称，热力学第二定律在 “自然法则中处于最高地位”。他写道，任何反对该定律的理论都会“在最深的羞辱中崩溃”[18]。近100年后，爱丁顿还没有被证明是错误的。
 

参考文献

[1]J. Goold et al., J. Phys. A: Math. Theor. 49, 143001 (2016).[2]C. Cercignani, Ludwig Boltzmann: The Man Who Trusted Atoms, Oxford U. Press (1998).[3]W. C. Myrvold, Stud. Hist. Philos. Sci. B 42, 237 (2011).[4]V. Serreli et al., Nature 445, 523 (2007).[5]H. Leff, A. F. Rex, eds., Maxwell’s Demon 2: Entropy, Classical and Quantum Information, Computing, CRC Press (2002).[6]O. Shenker, M. Hemmo, Entropy 22, 269 (2020); J. Norton, Stud. Hist. Phil. Sci. B 42, 184 (2011).[7]D. J. Bedingham, O. J. E. Maroney, New J. Phys. 18, 113050 (2016).  [8]N. Y. Halpern, Sci. Am., May 2020, p. 60.[9]H. E. D. Scovil, E. O. Schulz-DuBois, Phys. Rev. Lett. 2, 262 (1959).[10]A. Levy, D. Gelbwaser-Klimovsky, in Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions, F. Binder et al., eds., Springer (2018), p. 87; B. Gardas, S. Deffner, Phys. Rev. E 92, 042126 (2015).[11]J. Klatzow et al., Phys. Rev. Lett. 122, 110601 (2019).[12]A. Einstein, Autobiographical Notes, P. A. Schilpp, trans. and ed., Open Court (1979), p. 31.[13]K. Friston, Nat. Rev. Neurosci. 11, 127 (2010).[14]J. C. Maxwell, “Diffusion,” in The Encyclopædia Britannica: A Dic- tionary of Arts, Sciences, and General Literature, 9th ed., vol. 7, Adam and Charles Black (1877), p. 220.[15]P. W. Bridgman, The Nature of Thermodynamics, Harvard U. Press (1941), p. 214.[16]Ref. 14, p. 220.[17]S. Lloyd, Nat. Phys. 2, 727 (2006); S. Popescu, A. Short, A. Winter, Nat. Phys. 2, 754 (2006); S. Goldstein et al., Phys. Rev. Lett. 96, 050403 (2006).[18]A. S. Eddington, The Nature of the Physical World, Cambridge U. Press (1928), p. 74.

本文经授权转载自微信公众号“集智俱乐部”。