2025年6月25日，是我的博士论文指导老师李天岩教授逝世五周年。三天后的28日，将迎来他的八十周岁诞辰。

五年前，在他离世的那个早晨，弟子们马上举行网上追思会的沉重哀悼气氛至今还弥漫在我的脑海中；十年前，在密歇根州立大学数学系为他庆祝七十寿辰的师生欢乐场景也依然在我眼前不时浮现；再向前十年，在台湾新竹清华大学理论研究中心“庆祝李天岩教授六十周岁国际学术研讨会”上拍下的那张师门群聚照，一张张笑脸栩栩如生地反射出充满“李天岩学术家族”特色的亲密师生情缘……现在，思绪万千的我把对他的感恩和思念之情，聚焦在几十年中他对博士弟子们的一生影响中。

人在一生一世中受到各种影响，有幼儿直至少年时期的父母影响，有读书时代的师长影响，有无孔不入的社会影响，有潜移默化的好友影响。这些来自四面八方的复合影响，有正有负，就像机械工厂锻造车间的冲床，将我们捶打成不同类型之人、不同善恶之心、不同追求之辈、不同发育之躯，而选择了不同的价值观念和生命轨迹。

然而，就我自己可以记忆的六十年人生历程，撇开阅读习惯这个功率极强的影响力不谈，抚育孩子长大的父母和教育学生成才的教师对于个体可能是公认的两大“影响因素”。我在回忆先母的文章《母亲的手》中写道：“她不仅潜移默化我一生爱书，而且言传身教我莫为功利；她不仅树立我远大理想，而且鼓励我永不退缩；她不仅教育我礼貌待人，而且告诫我勿忘他恩；……”从中可量度出家长对子女的影响力。但是，对于未来将走向探索学问之路的大学生和研究生，亲炙于优质导师的治学之道和做人原则，对其职业的影响毫无疑问是最具决定性的。

在李天岩教授几乎所有的弟子眼里，他就是这样一位言行完美结合的导师：在对待治学的态度上，他为学生做出表率；在用于钻研学问的时间上，他比学生还要投入；在将后学者带入新的研究领域时，他慷慨播撒思想的种子；在教导怎样解释数学的过程中，他对学生倾情传授演讲技巧；在每周举行的弟子讨论班上，他常常跳上讲台示范一个概念的自然登场。他沉浸数学未知世界探索其中奥秘时显示出的忘我状态，他在课堂讲授数学声情并茂迸发出的迷人激情，四十年间影响了他一批又一批的弟子和学生们。

今天，在李天岩教授离世五周年之际，让我梳理这段历史中自己比较熟悉的那几根经纬，踏着他所留下的研究足迹，回放对年轻学子或许有启迪意义的几首学术乐章，以典型而具体的代表性人物故事，追忆他是怎样深刻地影响了众多的弟子和广义的学生。

在那之前，博士生李天岩独立或跟随导师约克所做的所有研究都属于微分方程与动力系统领域，这是纯粹数学的一个重要分支，对自然科学和工程技术有着广泛的应用价值。此刻的李天岩已经完成了“周期三则意味着混沌”这一“约克猜想”的初等微分学证明，但日后让他声名显赫的“李-约克混沌定理”还要等到1975年的圣诞之月，才在大众杂志《美国数学月刊》中横空出世。

为何这时以纯粹数学研究见长、已有数个不平凡成果的李天岩，一下子修起了某些纯粹数学家都比较轻视甚至轻蔑的计算数学课程？

这是因为，在上世纪七十年代初的美国，高等院校新增教职对于刚刚出炉的新科博士，极难获取。当时是与九十年代初同样艰难的大学教鞭稀少期。结果是许多来自中国台湾的留美博士生，获得博士后因在美国学术界很难找到职位而最终打道回府。为了帮助弟子留美工作多一条后路，即便拿不到大学教鞭也有可能靠实用学科的知识在工业界谋到一份差事，那学期约克教授便让李天岩去凯洛格教授的课堂旁听，学一学数值求解非线性代数方程组有用的理论和方法。

差不多九年后的1982年，我在南京大学的教学大楼里与硕士导师何旭初教授的几个同门弟子及南京师范学院的一位旁听研究生，作为最优化理论研究方向的专业基础课，注册修读了李天岩教授早九年旁听过的同名研究生课程。开讲此课的沈祖和老师很会教书，他选用的教材，恰好就是1970年出版的马里兰大学计算数学家James M. Ortega（1932-）和Werner C. Rheinboldt（1928-2024）两教授撰写、现已成为经典的一本厚书《多变量非线性方程组的迭代解》（Iterative Solution of Nonlinear Equations in Several Variables）。我没问过李教授当凯洛格教授于1973年讲授该课时有没有将其本校同事的这本著作指定为教材或列为参考书，但当我于1986年留学密歇根州立大学数学系读博士学位而修了几年课，才知道美国大学和当时的中国做法经常不一样：许多教授讲授的研究生课程没有专门的教科书而只列出参考书，有的连参考书都没有，全靠教授依据自己准备的讲义，靠他的三寸不烂之舌来兜售知识。可是，这种看似不甚统一的做法，却至少会让有创造性思维倾向的一些听课者受益无穷。

为什么呢？因为那部分研究型教授在教学中由于知识常新，会有意或无意地将与课程内容相关的思想浪花泼洒在学生的头顶上，而这正是凯洛格教授在班上所做的。他的课中有一节讲的是布劳威尔不动点定理。这是以其主要发现者荷兰拓扑学家布劳威尔（L. E. J. Brouwer，1881-1966）的名字命名的一条大定理，其叙述语言稍微简单一点的某个版本是：n维欧几里得空间中的单位闭圆球到其自身的任何光滑映射必有不动点。既然此定理极其重要，且应用十分广泛，从它问世后的几十年间人们找到了多种多样的证明也就不足为奇了。沈祖和老师发给我们听课研究生的教科书中有一章，专讲非线性映射的度理论，作为该分析学重要数学工具的一个直接应用，布劳威尔不动点定理自然而然地就被推理了出来。我当时学习完这一段内容后，虽然惊叹于度理论之精妙，却根本想不到，也可能无从想起，从这里可以再闯出一条探索之路来。盖因那时的我还没有懂得怎样做研究，同时，周围的教学环境也没能向我提供浸润于创造性思维的良好机会。

然而，凯洛格教授却独辟蹊径，没有按照标准教科书中现成的方法在黑板上抄下证明，而是从期刊中拿出加州大学伯克利分校数学系的赫希（Morris Hirsch，1933-）教授十年前在美国数学会的期刊上发表的一个简洁反证法，展现给班上的学生。赫希的推理过程可简单叙述如下：倘若将闭圆球映到自身的光滑映射没有不动点，就可定义一个将闭圆球映入到其表面（维数比球体少一的球面）的一个光滑映射，它具有下面的性质：球面上每一点在该映射下动也不动；换言之，这个值域比定义域维数少一的映射限制在球面上是个恒等映射。这却和微分拓扑学中的一个基本结果相矛盾。下图对二维闭圆盘情形展示了赫希反证法中所构造的将闭圆盘映到圆周上的那个光滑映射：

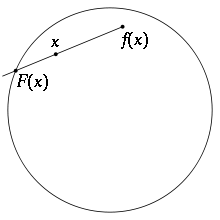
在图中，由于反证法假设，闭圆盘上任一点x不等于f(x)，其中f是给定的将闭圆盘映到自身的光滑映射，故可将从点f(x)到点x的有向线段延长到与圆周的交点F(x)。这就构造出了一个光滑映射F，它将闭圆盘映到圆周，并保持圆周各点不变。但微分拓扑学中的一个基本事实却阻止了它成真。

仅仅旁听凯洛格教授这门课的中国青年李天岩，却没有像正式注册此课的其他研究生一样，对赫希的证明“一听了事，下课就走”，而是深深陷入探索性的苦苦思索之中。这或许就是浅尝辄止学习者和刨根问底学习者的分水岭。他在想，虽然那个将闭圆球映到圆球面的映射（在上图中标记为F）无法在整个闭圆球上的每一点处都能有定义（因为不动点存在！），却能在将闭圆球中所有不动点（至少有一个）去掉之后的那个集合上处处可定义，那么，根据微分拓扑学中的沙德定理，随机地在圆球面上取一点（所构造映射的“正则值”，在球面上几乎处处存在），它在这个余维数为一的映射下的逆像是一条维数为一的光滑曲线，它起始于该点，最终将会趋向于原先映射的所有不动点组成的集合。如果从所取初始点出发，数值上沿着这条曲线向前推进，就有可能计算出一个不动点来。这同时也可形成布劳威尔不动点定理的一个“构造性证明”。

这个将赫希反证法再向前推进了一步的思考结果，播下了现代同伦延拓法的种子。李天岩将他的新想法告诉了导师约克教授和授课老师凯洛格教授。他们都支持他利用电子计算机实战他的新点子。经过两个月的紧张数值试验，之前从未上过计算机的纯数学博士生在计算数学史上基于微分拓扑学，第一次算出了布劳威尔不动点。

年轻时的李天岩教授是够幸运的，因为他在博士生阶段开创了一个新领域——现代同伦延拓法。但是他的幸运首先建立在他的主观能动性之上：不是被动地接受现成知识，而是主动出击，敏锐发现新的突破口，创造出新的知识。而这个学术机遇也跟凯洛格教授分不开。如果这位教授仅仅满足于按部就班地照本宣科，可能听课的学生不易从中获取启动创造性思维的第一推动力。所以，好的老师，尤其是论文指导老师，往往能激发出学生对探索未知的好奇心和成功欲。

李天岩教授对他的博士论文导师约克教授推崇备至，认为自己对数学及其研究的品味极受后者的影响。赴美留学前，尽管在台湾清华大学数学系本科四年的成绩单拿出来十分耀眼，几乎门门五分，但他却在几十年后的文章《回首来时路》中，剖析自己当年对数学“一窍不通”，只会“背定义背定理”，而大学成绩自称“C或C以下”的约克教授，在他眼里却是数学武林中的“一代宗师”。

约克被弟子如此仰视，一个重要原因是，如同他十年前在电邮中告诉过我的：“我在高中起就学会了怎样学数学”。这个怎样学数学的真谛，再用他对我说过的另一句话说，就是“理解重要定理证明中的关键想法比理解定理本身更重要”。我想，正是透彻理解了混沌之父洛伦兹（Edward N. Lorenz，1917-2008）关于长期天气预报不可预测性的那篇论文《确定性非周期流》（Deterministic Nonperiodic Flow）中的关键想法，他的大脑中才提炼成“周期三意味着混沌”的伟大猜想，而他的弟子则抓住了这个猜想反射出的迭代内涵，运用微积分手段破解了它，变合理猜想为深刻定理，三十年过后被卓越的理论物理学家戴森（Freeman Dyson，1923-2020）在其“爱因斯坦讲座”文章《鸟与蛙》（Birds and Frogs）中赞叹为“数学文献中的不朽珍品”。

李天岩教授年轻时的另一大数学贡献，也和约克教授的创见及他自己的眼光相关。约克与其亲密合作者波兰数学家拉速达（Andrzej Lasota，1932-2006）在1973年发表了一篇现代遍历理论的重要论文，回答了被后世称为“数学科学家”的氢弹之父乌拉姆（Stanislaw Ulam，1909-1984）提出的一个数学问题——“区间上的逐片单调映射是否具有绝对连续不变测度？”他们证明：对于逐片拉长的映射回答是肯定的。在其存在性定理的证明中，约克发现的关于有界变差函数的一个不等式——后来被称为约克不等式——起了关键性作用。

这类映射现在称为拉速达-约克类区间映射。刚获得博士学位不久的李天岩读到导师的这篇合作论文时，没有仅仅停留在理解文章的定理和结论上，而是想得更远：在拉速达-约克类映射绝对连续不变测度的存在性得到保证后，数值上能否方便地将它算出来？这当然属于计算数学的范畴，可惜的是，不少纯粹数学家不大瞧得起计算数学这门应用性极强的学科，他们的姿态有点像美声唱法歌唱家对待流行歌手，以为后者不能登大雅之堂，所以他们中的许多人鲜有考虑计算之想。然而，约克教授于2005年借庆祝弟子六十岁生日之际，在台湾接受数学家刘太平教授采访时说道：“计算能导致伟大的发现”。当然，只要读一读刚刚去世的美国应用/计算数学家拉克斯（Peter Lax，1926-2025）的学术履历，瞧一瞧上面所罗列的国家科学奖、沃尔夫数学奖、阿贝尔奖等大奖，部分纯粹数学家对计算数学的那些轻视之语大概就应该收回。由于发明了现代同伦延拓法，此时纯粹数学出身的李天岩博士可能自告奋勇担当一位计算数学家了。

一旦又有了新的想法，他就全力以赴地沉浸其中，很快构造出一种用于可积函数空间的算子方程数值逼近法。利用已驾轻就熟的布劳威尔不动点定理，他确认了该算法计算近似不变密度函数的合理性，并采用了他导师发现的那个新颖的约克不等式，证明了他的逐片常数投影密度计算法在可积函数空间中的强收敛。更由于他的方法恰好也是乌拉姆在自己1960年出版的书《数学问题集》中提出的矩阵逼近算子法，他实际上对一类区间映射解决了关于书中提出的乌拉姆方法收敛性的所谓“乌拉姆猜想”。李天岩教授的这项成就使他和乌拉姆一同成为计算遍历理论这一新兴应用学科的两位主要奠基者。

1976年，硕果累累的李天岩博士被密歇根州立大学数学系聘为助理教授，此时他的身体状况已经逐渐变坏；事实上，到他去世为止，他与肾脏疾病搏斗了半个世纪。然而他没有停下脚步，常在医院里思考数学。

1986年1月2日，是我到达留学美国目的地的第一天。在当晚祖国同胞招待我的晚餐上，李天岩教授的一位博士生告诉我，本系一些教授在研究之路上寸步难行，却看到李教授的论文预印本如同雨后春笋不断冒出。从李天岩教授1982年带出的第一个博士开始，他的创造性研究风格也极大地影响了他的弟子们。

李教授常提及朱天照的第二个用意，是介绍这位优秀弟子在数值代数领域率先用同伦思想处理矩阵特征值问题的新颖想法。我们这几个大陆弟子同年进校后，最后写出的博士论文除了两人之外，都聚焦于矩阵特征值同伦延拓法计算，其最基本的想法出现在朱博士早他们几年发表的那几篇论文中。同伦延拓的思想用于计算数学的不同领域，就会催生出能保证全局收敛性的新算法，对于特征值问题，它还有计算过程可以实现并行化的额外优势。李教授深信，矩阵特征值同伦算法具有与在数值代数中占有老大地位的经典QR方法一比高低的潜能。于是，他率领手下兵马在那些年中，为实现这一目标做出了令人瞩目的成绩。

作为李教授最优秀的弟子之一，朱天照在获得博士学位六年后就晋升为正教授。而在正常情况下，从助理教授到副教授，在研究型大学一般需要六年的“试用期”，即经过自下而上的系、院、校三级投票结果为正时，所在大学就会相信被晋升者有了可以永久聘用的资格，而不再“试用”。朱天照在计算和应用数学领域中的众多学术贡献，包括对于特征值反问题的深入研究并出版了专著。我在读博士阶段的几年中只见过他一次，那次他应导师之邀从他正在访问的位于芝加哥的国家实验室驱车回到母系，做了一场学术报告，专论离散迭代算法与连续动力系统之间的姻缘关系。他关于这个论题和特征值反问题的综述性文章都刊登在美国工业与应用数学学会的期刊SIAM Reviews上。

李天岩教授后半生的主要研究领域是多元多项式方程组数值解。求联立多项式方程的共同零点是代数几何的一个中心问题，同伦算法成为数值求解的一件利器。在同我一批的弟子中，以七七级考进吉林大学数学系的王筱沈是他在这一领域的学术传人之一。王筱沈兄弟四人中有三人在美国当了数学教授，他们的父亲是中国有名的数学家王柔怀教授。1986年秋季学期开学前，刚进校几天的王筱沈就去考了本系博士生撰写学位论文前两大必要考试之一的“资格考”（第二个过关考试叫“预备考”，都考两门）。因为我和他同进考场，看到李教授跨进教室查看他“考得怎样”，其情节被我写进了《走出混沌：我与李天岩的数学情缘》书中。当善于发现学生天赋资质和用功程度的李教授了解到这位长我五岁者读书时和他一样是个“拼命三郎”时，就对他额外加码好好栽培了。

我在上述的书中这样回忆王筱沈：“李教授看出他的学术素质、研究潜力和用功精神，在他一通过博士预备考后，就交给他受过格罗滕迪克（Alexander Grothendieck，1928-2014）栽培的美国代数几何学家哈茨霍恩（Robin Heartshorn，1938-）的名著《代数几何》（Algebraic Geometry），里面的语言将在弟子未来的职业生涯中不停地挂在嘴上或写进文章里。密歇根冬季的冰天雪地来得早却去得迟，地面是一片白雪皑皑。王筱沈除了白天去校修课教书，每天在家吃完晚饭后，同样骑着自行车飞驰到办公室，继续沉浸在代数几何的王国里，直至夜深人静骑车回家。”

对代数几何下了苦功的王筱沈将这套纯数学的艰深理论运用于数值求解多项式系统的同伦算法，取得不俗的成绩。他进攻学问的精神和诚实做人的品质一直深受导师的喜爱，他们不仅合写研究论文，而且王筱沈夫妇位于阿肯色州首府小石城的家很可能是李教授光顾得最多的弟子之家。

本科和硕士学位均在武汉大学获得的曾钟刚，是另一个在研究的开拓性探险上继承了导师衣钵的例子。在李教授的所有博士生中，我和曾钟刚在两人出国前就有过通信交流，介绍人是中山大学数学系的王则柯老师，因为八十年代初王老师从访学的美国引进了单纯不动点算法这一新的领域，而曾钟刚则先于我接触到该研究课题。我们于1985年6月初分别从南京和武汉去了中山大学，与首次访问祖国的李教授见面，一同聆听了他为时一周的若干次讲座和演讲。那次曾钟刚和李教授同游中山纪念堂的合照，被我放进了回忆录《走出混沌：我与李天岩的数学情缘》里的第一章。

几十年来，曾钟刚钻研学问的特点是甘坐冷板凳，深入问题的心脏，不达目的绝不罢休。他的博士论文研究集中在用同伦思想计算一般矩阵的特征值和特征向量，这是在同门师兄朱天照、Noah Rhee（韩国名字是李弘九）先前工作的基础上，对李教授所开创的代数特征值问题同伦延拓法的继续推进。在进一步深入探索的过程中，他自然而然地面临对计算数学而言极端困难的一个棘手问题：怎样有效地计算代数方程的重根？

由于计算过程出现各类误差的不可避免性，数值处理重根问题的困难性可用一个日常经验打比方：如果将一件小物品放在桌面的边界之内，则该物被稍稍移动一下位置后，依然还会在桌面上而不至于掉下地来；然而，如果将它放在桌面的边缘处，则微小的一个移动都有可能致使它掉在地上，除非将它向着桌子的中央移动。这说明，东西放在桌面的内部是安全的，而放在边界上则是危险的。用此来比较代数方程的单根重根，“桌面内部”相当于“单根”状态：在方程参数的微小变化后单根依然保持单根；“桌面边缘”类似于“重根”情形：不同方向的微小变化会引起重根的不同变化。

在矩阵理论中也有类似的现象：可逆矩阵的小小扰动不改变矩阵的可逆性，因而从可逆矩阵到其逆矩阵的变换是连续的，即矩阵元素的小变化导致逆矩阵元素的小变化；然而奇异矩阵就复杂多了，某些小扰动可以保持矩阵的秩，但另一些小扰动却可以增加秩，因此从一般矩阵到其广义逆矩阵的变换是不连续的，可以证明这仅仅是个“上半连续”的变换。

如果在数值上能卓有成效地克服重根问题带来的困难，便能成就计算数学的一个大突破。曾钟刚从导师那里继承了进攻难题“不到长城非好汉”的气概，埋头苦干了好几年，终于想出了一种“流形投影”的妙法，成功解决数值计算重根困扰计算数学界的这一个难题。李教授曾经告诉过我，在那几年中，曾钟刚没有满足于做些容易发表论文的小研究，事实上这样的文章他五六年间好像一篇也没有发表过，集中精力专攻“重根问题”，最终是不鸣则已，一鸣惊人，他的优秀成果发表在计算数学的名刊上，他的研究思路得到美国科学基金会的赏识而获得基金支持。他关于重根计算的开创性文章获得美国计算机协会符号与代数计算2003年会的杰出论文奖。

事实上，这篇内容厚实的杰作，如果愿意的话，可以分成三篇写：多项式最大公因子数值计算的第一个算法；多项式的根的重数计算；用已知重数精确计算重根。李教授对弟子说，你要是分成三篇，都是一般渐进文章，但把三篇写成一篇就是经典。后来果然成了获奖文章，首次实现多项式重根精确计算。前几年，曾钟刚继续将降服重根的思想推广到奇异导数矩阵情形下的牛顿迭代法并获成功。目前的他正在撰写专著，总结他在这个领域中的开创性工作。

长期情系学问不折不挠的曾钟刚身上，散发出李天岩教授对他深入骨髓的影响，他也因此深得导师的赞许和期待。离开师门后的近三十年，他与李教授一直保持学术交往，结伴探索，保持浓厚的师生情谊。在和我同期的四五个师兄弟中，他任教的大学离母校最近，他也常常开车四小时回校访问加看望导师。《走出混沌：我与李天岩的数学情缘》书中的最后一张照片，是他于2020年1月18日驱车前往密歇根州东兰辛市探望老师，两人一同观看美式足球赛时留下的合影。五个月再加一周后，李教授溘然长逝。

李天岩教授的学术人生“影响因子”遍及他的所有弟子，他们无论是在大学教书或管理，还是在公司负责研发，都实践着导师对他们的教导。我同批的师兄弟中，就有两位获得任教学校“大学杰出教授”的头衔。他几十年不断的“李教授师生讨论班”，从来不会让学生仅仅停留在对所报告学术论文的定理陈述、证明逻辑以及研究结论的肤浅了解上，更不允许报告人缺乏准备地走上讲台匆匆报告可能自己也没有真正搞清楚的一篇文章。他时刻强调的是，每一个演讲者都必须搞明白定理条件和结论背后的基本思想。在他的调教下，经过讨论班严格训练的前后跨度三十年的二十多位博士生，大都成长为会讲数学、会提出问题并能解决问题的新一代学者。

李天岩教授虽然已离开人世整五年，但他的治学思想和人格魅力不仅对他亲传的弟子和教过的学生继续发生影响，同时也对知晓他一生传奇故事的广大读者带来追求真理的动力，鞭策人们不畏困难，勇往直前。长期的疾病缩短了他的寿命，但他的求知精神却长驻人间。李天岩教授将永远被人铭记与敬仰！