法国数学家André Weil是20世纪最伟大的数学家之一，他的研究涉及诸多数学领域，主要集中于在数论和代数几何。他是数学界的传奇人物，创建了布尔巴基学派，并几乎见证了20世纪的数学发展。本文为著名数学Jean-Pierre Serre（三大数学奖得主）在Weil去世后为纪念他所作，主要介绍Weil的学术工作。 

翻译 | 冯克勤

校对 | 戴新生 

André Abraham Weil，1906.5.6-1998.8.6

André Weil于1998年8月在普林斯顿去世，终年92 岁，因为他夫人 Eveline先离开人世，自己因为年纪大身体衰弱，他的最后几年是在忧伤中度过的，死亡对他来说或许是一种解脱。

法国科学院要我向诸位介绍他的生平和工作，以表悼念之意。

他于 1906 年生于巴黎一个犹太人的家庭，父亲是医生，原籍阿尔萨斯。母亲生在俄国，原籍奥地利。他有一个比他小三岁的妹妹Simone，兄妹一直非常亲近，一直到 Simone于1943 年去世。后来Weil曾为出版他妹妹遗留下来的一些文稿而尽力。

人们发现他的《学徒回忆》([1991]^[1])中精彩地叙述了他所受到的严格和比较传统的教育，总而言之：对古典语言（拉丁文、希腊文和梵文）强烈地爱好，并且很有数学天赋。这使他在 1922 年十六岁那一年进入了高等师范学校。1925 年毕业时通过了法国教师的学衔考试，尽管理论力学考试交了白卷，因为他觉得这不是数学的一部分。他去了意大利，以后又到德国，遇到了那个时代一些真正优秀的数学家：Hilbert，Artin，von Neumann，Siegel。他在 1928 年二十二岁时完成了学位论文，后来去印度 Aligarh大学当了两年教授，印度学学者 Sylvain Levi 帮他获得这个职位；他在 College de France曾跟Levi学习过梵文。后来在1933年到1939年在马赛和斯特拉斯堡任教。在斯特拉斯堡时与昔日在师范学校的朋友（Henri Cartan，Jean Dieudonn，Jean Delsarte等）创建了Bourbaki 小组。1939 年二战爆发时他去了芬兰；他被当作苏联间谍差一点被枪毙，后来他被转到法国监禁在Rouen。在对他的不服兵役加以谴责之后，他不久获得自由，在经历了各种惊险后（都写在《学徒回忆》中），他于 1940 年去了美国，居留几年后又去巴西呆了两年，一直到 1947 年才得到跟他水平相称的职位：芝加哥大学教授。从1958 年起他到普林斯顿高等研究院，在那里度过了他一生的最后四十年，这个研究院对他非常合适，给他充分的从事研究与讲课的自由（如果他愿意，也可以不讲课），也有高水平的教授同事和访问人员。（他的位置就象我们的College de Erance 一样是终身的，我一直希望他能在此占据一个数学讲座！但这不是想做就能做到的。)

要想介绍 Weil 的学术业绩，我只需列举他得到的某些头衔（或者说是他接受的一些头衔）他是美国科学院院士和伦敦皇家学会成员，他是 1979 年 Wolf奖获得者（同时得此奖的是 Jean Leray，比 Henri Cartan早一年得）他于1994 年获得京都大奖^[2]，最后这个奖令他特别感到高兴，因为他一直和日本数学家保持良好的关系。

我现在转到正题上来，即介绍他的工作。他在 1926 年于Comptes rendus上发表了第一篇摘要性文章。在此后的五十年里出版了十二本书，发表了许多论文，用法文和英文写成，有的还用德文。这些文章收集在他的三卷数学论文集中，Springer出版社于 1979年出版。Weil对每篇著作都写了精确的评论，或解释这些论文的产生背景。

我不可能按专题对这些著作加以分类，因为涉及的专题太多。当然，也可按美国方式列出关键词：zeta 函数，Siegel，有理点，阿贝尔簇，……这可能有趣，但不严肃。我觉得唯一的可能是按时间次序，何况他的选集就是采取的这种方式。

1. 从 1928 年他的学位论文开始。它属数论，更具体说是不定方程，即代数簇上的有理点。那个时代所知道的唯一方法是费马发明的无穷下降法，使用这种方法总是要进行具体的计算，虽有些奇妙，但缺点是每个特殊情形都要算。Weil 首先看出在这些计算的后面有一个一般的原则，他称之为“分解定理”。这个定理在代数性质（原则上比较容易）和算术性质（比较困难）之间实行某种转换。由此得到了一个结果，现在叫作 Mordell-Weil定理：阿贝尔簇在一个给定数域上的有理点群是有限生成的，证明很不容易，那时的代数几何还没能提供必要的工具。幸运的是，Weil在师范学校时就深入地了解黎曼的著作，用分析工具（theta 函数）来代替他所缺乏的代数方法，他最终达到了目的。

“目的”一词不够准确。事实上，正如Weil的几乎所有工作，它涉及一个“起点”，由此出发可以解决其它问题，这篇论文引发的是以下一些问题：

——证明亏格大于0的仿射曲线只有有限个整点，这是以后由 Siegel 做出的，组合了Weil 的思想和超越数论中的结果。

——证明 Mordel 猜想，即亏格大于 1的曲线上只有有限多有理点，这是五十五年后由 Faltings 做出的。

——Mordell-Weil定理，Siegel定理和 Faltings 定理的有效（即明显）定量结果。1966-68年期间，Baker只对 Siegel 定理的特殊情形给出有效的定量结果；对Mordell-Weil定理和 Faltings定理整个问题仍未解决（数论学者们对此有极大的兴趣）。

2. 在这篇论文之后的几年里，他为 Mordell 猜想所引导研究了各种线索，其中之一是他在 1938 年所写的巨著《阿贝尔函数的推广》。这篇文章的表达形式是分析学，其意义本质上是代数学，而动机却是算术！（人们可以这样的问：除了Weil 和Siegel之外，有谁在1938年能看懂这篇文章？）这篇文章成功地用于阿贝尔簇，特别是用于曲线的雅柯比簇（Jacobian）。Weil指出应当从阿贝尔的框架出发，雅柯比簇将秩为1（和0次）的向量从参数化（换句话说，要从GL₁到GL_n，这是他喜欢的一个主题）。他和其他人只知道解析向量丛，还缺乏代数向量丛，十二年之后才诞生代数向量丛（也是由Weil给出的）。这并没有阻碍Weil，他引进了与向量丛等价的概念，即“矩阵除子类，（追随黎曼和庞加莱）用分析方法证明了黎曼—洛赫公式和我们现在称为“对偶定理”的结果（也叫作非齐性的黎曼—洛赫定理）多么漂亮的大手笔！但是定义这些丛还不够，他又研究它们的“参量簇”，用来代替雅柯比簇。从代数几何观点，这是一个涉及构造商簇的重要问题，在二十余年之后由Grothendieck 和Mumford 解决。Weil 只得到部分结果，大部分没有证明（但他所揭示的本质上是正确的），从而他不能给出任何算术应用。这是失败吗？不，因为在十五年后它可将黎曼—洛赫用于其他模型上，并由此构作出的参量簇，在其他问题上的影响也被揭示出来：Donaldson在微分几何中和 Drinfeld 对特征p>0的情形所作的工作。

3. 在我所讲的1928年-1940年这段时间，Weil不仅限于研究数论，下面是他的另一些研究活动。

——多变量复分析，引入一种积分作为柯西积分的推广，现在称为Weil积分（1932和1935年）；由此给出Runge定理的推广：若D是由多项式不等式定义的有界区域，则D是每个全纯函数对于紧收敛拓扑都是多项式的极限。.

——紧微 Lie群理论，用拓扑方法（Lefschetz公式）证明极大环面彼此共轭（1935年)。

——p-adic分析（这项研究还处于幼年时期），定义了p-adic 圆函数（1936年）。

——拓扑学，定义了一致空间（1937年）。

——在Hermann公司出版了《拓扑群的积分及其应用》一书（1940年）。书中以简洁的Bourbaki方式阐述了该理论被那个时期所接受的两个方面：紧群情形（特征的正交关系）和交换群情形（Pontrjagin对偶和傅里叶变换）。

4. 现在回到数论和代数几何，讲他在1940年的一篇重要的短文。

在1925-1940年期间，德国学者在Artin和Hasse的推动下，在代数数域和有限域上的单变量函域（用几何的语言则是有限域上的曲线）之间发现值得注意的类似。彼此都有zeta函数，都可提出“黎曼猜想”。对于函数域情形，Hasse 对亏格为1的情形证明了黎曼猜想。如何解决亏格大于1的情形？Weil于1940年在Rouen时就看出问题的解决方法：这个关于一维代数簇（即曲线）的问题应当利用更高维的代数簇（曲面和阿贝尔簇）以及采用（在复数域）拓扑或解析方法证明结果的方案：他于1940年投到 Comptes rendus的短文一开头便写道：

“我在这篇短文中打算概括地叙述有限域上代数函数论中一些主要问题的解法……”

这篇短文只叙述了证明轮廓，所有事情都建立在一个“重要引理”之上，这个引理是从意大利几何学派那里得到启发的，但是怎样证明它？Weil 认识到需要重新构造整个代数几何的定义和基本结果，特别是相交理论的结果（所缺少的同调理论用cycles的计算来代替）。于是他写了三百页（有些枯燥的）的巨著《代数几何基础》（1946 年）。而在二十年后这本书被 Grothendieck更巨大并且更枯燥的《代数几何原理》所代替。《基础》一书出版之后，Weil 便可证明曲线上的黎曼猜想，结果发表在1948年同时出版的两本著作《代数曲线和相关代数簇》和《阿贝尔簇与代数曲线》，经过八年和五百多页的著作，他在 1940 年所写的短文所提出的目标终于得到实现！

有哪些推论呢？首先，黎曼猜想有许多具体应用，,对于单变量的三角和能给出上界（1948 年）。例如下面的三角和估计（可用于模型式理论）
 

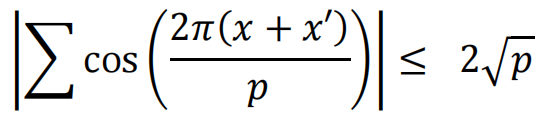
其中p为素数，x过整数 1, 2, … , p-1，而x'x=1 (mod p)。

此外，Weil不仅建立了代数几何的牢固基础，而且他发展了平行于利用 theta 函数的解析理论的阿贝尔簇的代数几何理论。阿贝尔簇是他多年来喜欢研究的课题（见他1952，1954，1976和1977年的论文），他还与谷山和志村几乎同时独立地得到复乘理论（1955年）。

5. 在曲线工作的指引下，及对单项式超曲面情形进行的具体计算，他于 1949 年提出了被后人称为Weil猜想^[3]的猜想。这是有限域上非奇异射影代数簇的一组猜想。它们假设黎曼，Lefschetz和Hodge等人的拓扑方法可用到特征p>0的情形；在这种看法之下，方程模的解数相当于不动点数，从而可用 Lefschetz的公式来计算。这种思想确实是革命的，唤起一代数学家们的热情（我可作为直接见证人），这也是随后多年代数几何学重大进步的一个源头。这项研究经过大约二十五年才完成，贡献者不是Weil，而主要是Grothendieck 和 Deligne。他们发展的方法是当今代数几何中最强有力的。应用于其他领域如模型式理论（正如Weil先前所预测）和决定有限“代数”群的特征（Deligne-Lusztig）。

6. Weil 的数论研究在 1951 年转到类域论。Artin在1927年证明一般互反律之后，类域论具有一种确定的形式。采用 Chevalley 的语言，其主要结果可以叙述成：数域K的最大阿贝尔扩域的伽罗华群同构于商群C_k/D_k，其中C_k是K的idele 类群，而D_k是它的连通分支（这样，可描述经提升或扩充后K的一些已知性质的情况，正如同有一个拓扑来描述由道路等价类所构成的复盖）。这个理论不尽人意之处是伽罗华群不是C_k而只是它的商群C_k/D_k。Weil 则提出一个想法：群C_k本身也应是某种意义上的伽罗华群（什么意义？我们不知道）。如果这是对的，则群C_k应当有好的函子性质（例如，若 L/K 是有限伽罗华扩张，则 Gal(L/K) 通过C_L应当有某种正则扩充。）人们想到是否可直接证明这些性质，而 Weil 做了这件事作为后来的发展，我还列举下面一些重要事情：

——研究了C_L的上同调群，这是类域论上同调方法的起源，由中山，Hochschild，Artin，Tate 等人所发展。

——定义了新的“Weil”群，由此得到新型的 L函数，Artin的非阿贝尔L函数和具有“大特征”的Hecke L 函数均为其特例。就像Weil所说的，实现了Artin和Hecke思想之间的联合。

7. 不久，Weil于 1952 年发表了数论中的“显公式”，1972 年又加以完备。这个公式（本质上别的专家们似乎也知道）把对素数的一些求和公式和对 zeta 函数零点的另一些求和式联系起来。Weil的写法很有建设性，比如说，从中明显看出阿基米德位和非阿基米德位之间的类比，这又是另一个Weil感兴趣的课题。更有趣的结果是把黎曼猜想归结为某个分布的正性。这种转化是否可用来证明黎曼猜想？现在预测还为时太早。

8. Weil于1940年到1965年还在微分几何领域做了许多工作，这些工作是：

——与Allendoerfer一起给出并证明了黎曼多面体的Gauss-Bonnet公式（1943年）。

——证明de Rham定理，（1947年给H. Cartan的一封信），全文于1952年发表。这对Cartan 的层论观点有很大影响（层论是Leray开创的）。

——调和形式和Kähler流形理论（1947年和1958年）。这是解析方法用于代数几何的基本工具。

——连络理论和引进“Weil代数”（1949年）。

——齐性局部空间和离散群的形变（1960年，1962年和1964年）。对于秩>1的单李群的商紧离散子群证明了刚性定理。.

9. 在五十和六十年代，Weil在由 Siegel 的工作所启发而提出的课题发表了一系列文章。Weil 在他的选集第二卷第 544 页所加的评注中说：“评论Siegel，对我来说，是当代数学家可以承揽的最有益的“任务”。注意动词“评论”：这是一个没有充分表达实情的说法^[4]。Weil的工作有:

——在1961年和1962年他系统地发展了由 Kuga 和玉河引进的 adele 方法。不仅重新证明了二次型的 Siegel定理，而且建议了许多新的问题。例如证明单连通群的玉河数为1（现在我们知道，由于Langlands，黎景辉和Kottwitz的工作，这问题的答案是肯定的）。

——他于1964年和1965年发表在Acta Mathematica的两篇重要文章中，对二次型和Siegel公式采取了新的观点。他引进并研究了一种新的群：metaplectique 群，及这个群的表示（现在称为Weil表示）Siegel公式表示成两个分布之间的等式，其中一个是Eisenstein类型的级数，而另一个则是 theta 函数的平均。这个结果不仅限于二次型，Weil 证明它可用于所有典型群。他在这个领域引进局部整体类型的定理（Hasse原则），并且决定出玉河数。

10. Hecke 的工作也启发着 Weil。他在 1947年《数学的未来》的一篇文章中已谈到欧拉积并说：“把 Hecke 的工作加以透彻的研究，对于我们进行数论和函数论的研究是极为重要的。”二十年后（1967年）他对 Hecke 理论作了决定性的贡献，证明了：狄里赫利级数和它的“扭曲”（tordues）的某些函数方程可用来刻画这些级数来源于模形式。以数学上的精确形式得出对应关系：

模形式狄里赫利级数。

Hecke证明了→，并且对level为1的特殊情形证明了←。Weil的新想法是利用torsion。他的理论最有意义之处是给出函数方程的常数随 torsion 的变化方式（即用张量）。

这项工作引起一系列发展，其中的一些是 Weil 本人作出的（1971年）。正是在这个地方产生了所谓“Langlands哲学”。其中一个结果是对于 1955 年由谷山提出的有些含混的猜想给出一个精确的形式。

根据这一猜想，Q上的所有圆曲线都应当是“模”曲线。而 Weil 则认为模形式的“水平”应当是对应椭圆曲线的“导子”，后者由坏约化性质所决定。这个论断可以通过计算加以定量地验证。1995 年 Wiles 在某种技术限制之下证明了这个结果，但没有最终解决。（译者注：谷山-Weil 猜想最终被完全证明）^[5]。

11. Weil 最后的一些著作与文章是关于数学史的。Weil长期以来对数学史感兴趣，Bourbaki的《历史注记》的某些篇章（特别是第1至3章单变量实函数中的微积分部分）可以作证。他的小册子《按Eisenstein和Kronecker 的方式论圆函数》（1976年）即是数学著作又是数学史著作。他说他是以十分愉快的心情写成这本书，而这种愉快也传递给读者！后来的著作则是实实在在的历史。特别要提出他的书《数论：从Hammurapi到Legendre 的历史》（1984年）。这本书描写了1800年以前的数论史，也就是说，高斯的《数论探究》以前的历史。但是他的讲演则涉及更广，向我们介绍了高斯、雅柯比、爱森斯坦、黎曼……人们从他那里听到的是数学，是数学家们生活的主要方面，而不是他们的私人生活和社会关系，只有思想史是重要的，这是多么清新的看法！写这样的书显然是很不容易的，需要有语言和文学修养（而 Weil在这方面很在行），还要能区分开哪些是真正的新思想，而那些只是标准的技巧（他在1978年一篇文章中表达了这种看法）。一个不懂数学的历史学家很难做到这一点（可参见他 1973年，1975年和1978年的文章）。

在我做完上述介绍的时候，我相信与 Weil 所做的相比，这些介绍是很浮浅的，他的著作在二十世纪数学中是独一无二的，即预见性的方面（Weil“看”得见未来）与古典的精致相结合。阅读和学习他的著作，和他一起共同讨论，是我数学生涯中最大的愉快。

[1]英译本《TheApprenticeship.ofa Mathematician》（一个数学家的学徒历程 ) Birkhauser. 1992.

[2]这是一个文化奖，奖励在人类文化上有杰出贡献的人。

[3]猜想的原文 Conjectures 是多数。

[4]言外之意：不仅是评论，还更应当学习。

[5]谷山-Weil猜想现在被一些人称为谷山-志村猜想，但 Weil 晚年把这件事看的很淡。他喜欢引用 Siegel的说法：阿贝尔作为形容词，第一个字母已被小写了，如abelian。