20世纪60年代,物理学家发现场论在描述强相互作用遇到了困难,只能依赖现在被称为散射振幅的方法粗略描述粒子的行为。后来一位年轻的意大利物理学家从Beta函数中得到了一个简单的散射振幅公式,它如此简洁,就像笑话中最好笑的笑点,吸引了物理学家极大的热情。它所蕴涵的对偶性质为人们导向了现代弦论。物理学家在给新的模型找到物理含义时,弦诞生了,但它所带来的“幽灵”问题,还依靠数学家趟过“怪物”(魔)群。
撰文 | 格雷厄姆·法梅洛
翻译 | 王乔琦
这个理论极有可能不正确,但我们还是会严肃对待它,因为它具有真正的数学魔力。
彼得·戈达德 (Peter Goddard ),2016
1983 年春天,粒子物理学家正在欢庆标准模型的最新成果一一实验学家观测到了传递弱力的全部3 种粒子,它们的性质与规范理论物理学家预言的分毫不差。不过,只过了15个月,物理学家就开始认真思考标准模型的一个潜在继任者了。按照这个全新的理论研究方法,宇宙的基本单元并非粒子,而是极其微小的弦。
本章介绍的就是弦论的起源。它是现代物理学史上被研究得最为深入但仍未被证实的理论。我们将会看到,一位意大利物理学家在寻找亚核粒子行为模式的过程中第一次捕捉到了通往弦论的关键线索。虽然这些后来被称作“对偶模型”(Dual models)的理论在描述自然方面只能算是差强人意,但它们的特性还是勾起了理论物理学家(后来还有数学家)的极大兴趣。这些模型的一大显著特征是一类此前从没有人注意过的数学对称性。正是这种对称性促使理论物理学家提出了超对称(Supersymmetry)的概念,而超对称则是我们这个故事中的重要角色。正如我们即将看到的那样,这种对称性光芒四射,在数学和物理学中都非常有用,因此,很多理论物理学家都觉得这一定是大自然宏伟计划的一部分,哪怕实验学家找不到证明它存在的任何直接证据。
对偶模型的贡献远不止于此,例如,它还提供了一个运用弦论从基础层面描述整个宇宙的新视角,这个视角很可能具有革命意义。1984年,对偶模型首次成了物理学家的主流观点,这一转变后来被称为“第一次弦论革命”。与每一次真正的革命一样,对偶模型也令大部分专家大吃一惊。在此前的10年中,亚原子领域的大多数研究都只关注少量所谓的基本粒子,它们似乎都比较符合标准模型的描述。对许多物理学家来说,对偶模型的研究更像是一种家庭手工作坊:有一小部分聪慧的理论物理学家参与其中,要用到许多艰深的数学知识,但似乎得不出什么成果。在深入了解第一次弦论革命之前,我们先把时钟拨回20世纪50年代末 60年代初,去看看一种研究亚原子世界的冷门老方法是如何以更加高级的形式重回舞台中心的。这对我们后续的故事颇有指导意义。
从一个简洁的公式开始
“1959年的时候,有很多人觉得场论就是垃圾,”标准模型先驱阿卜杜勒·萨拉姆(Abdus Salam)后来回忆说,“且只有蠢人(指他自己)才会讨论像规范场论这样的东西。当时,许多顶尖理论物理学家认为,一些亚原子粒子无法用麦克斯韦发现的场论的现代版本解释,哪怕现代版本的场论得到了狭义相对论、量子力学和特定对称性的强化。将场论应用于受到强相互作用约束的粒子(如原子核中的质子和中子)时尤为困难。这类粒子之间的相互作用极其强烈,以至于场论的标准研究方法失效,无法做预测性的计算:唯一的希望似乎是运用现在人们称为“散射振幅”(Scattering amplitude)的方法粗略描述这些粒子的行为。20世纪60年代小部分理论物理学家正在研究这些振幅,试图阐明它们的数学性质以解释粒子加速器得出的实验数据。
以色列的魏茨曼研究所有一个专门从事散射振幅研究的小组。1968年6月前后,第一个对偶模型就在那里诞生,提出者是年轻的理论物理学家加布里埃莱·韦内齐亚诺(Gabriele Veneziano)。这位随和的物理学家当时26岁,刚刚博士毕业。韦内齐亚诺后来回忆说,他当时正在研究所内的咖啡吧小憩,却发现自己不自觉地展开了一场“思想实验”,深入思考描述π介子间碰撞的散射振幅会是什么样子。在笔记本上整理想法的时候,他突然想到了一种特别简单的振幅数学公式,涉及一种 100多年前的数学物理系学生就已熟悉的数学函数。
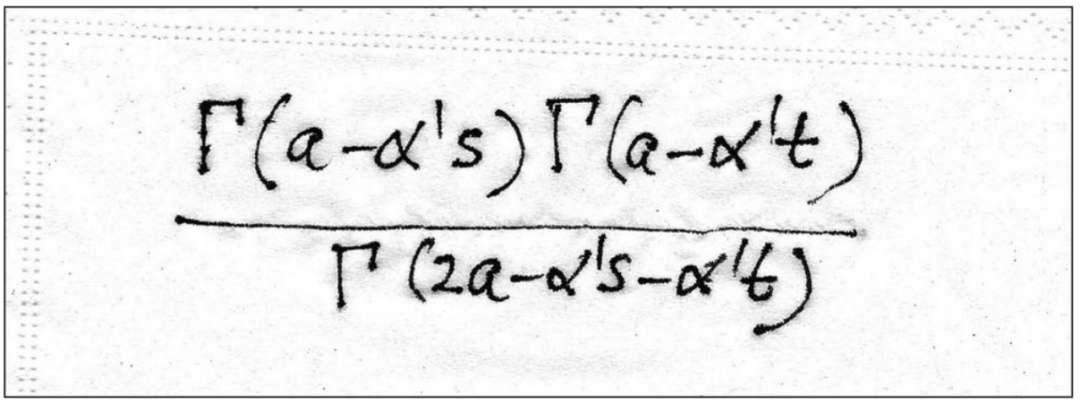
韦内齐亚诺的公式描述了某些强相互作用粒子间的碰撞。1968年6月前后,韦内齐亚诺第一次在纸上草草写下的这个公式(图中展示的是韦内齐亚诺手写在纸巾上的版本)后来被视为现代弦论的萌芽。这个公式的特点是结合了三个用希腊字母伽马(Γ)表示的相同的数学函数。式中的符号s和t与各粒子的运动状态有关,其他符号都代表常数。
散射振幅公式价值连城,也让韦内齐亚诺成了粒子物理学界的名人。虽然他这个公式的本意并不是解释实验结果中的细节问题,但它极好地解释了实验学家在观测强相互作用粒子碰撞行为时发现的大多数关键趋势。在此之前,从没有人见过哪个公式能做到这一点。对此,韦内齐亚诺“相当兴奋,但又有些紧张不安”,因为这个公式看上去实在太好,令人难以置信。这是幻觉吗? 它会不会其实没有任何意义?几周后,韦内齐亚诺在造访欧洲核子研究组织实验室理论部时,同那里的几位同行讨论了这个公式。他们中的很多人都非常惊讶,亚原子散射领域的这么多已知内容竟然可以浓缩到如此简洁的数学表达式中。韦内齐亚诺在都灵举办的一个研讨会上做了报告之后,颇有影响力的物理学家塞尔焦·富比尼(Sergio Fubini)对这个异常简洁的公式赞赏有加,称它就像是“一个非常好的笑话”的笑点所在。
韦内齐亚诺在受到富比尼的鼓励后,决定发表这个公式。相关论文正式发表于9月1日,当时他正在维也纳同近1000名物理学同行一道参加第14届国际粒子物理学大会。韦内齐亚诺的公式成了众人讨论的焦点,成了一个神奇的主题。多年以后,许多理论物理学家仍旧记得自己第一次遇到这个公式时的场景。物理学家戴维·奥利弗(David Olive)回忆说,他第一次听到韦内齐亚诺介绍这个公式是在奥地利首都中心霍夫堡(之前是奥匈帝国皇宫)恢宏的宴会厅举办的次会议上:“虽然场地的音效很差,但这段经历改变了我的人生。”不过,和许多重大科学进展一样,外行人并不理解物理学家这次又在大惊小怪些什么。韦内齐亚诺既没有发现新的定律或原理,也没有解释那些扑朔迷离的实验观测结果,更没有做出什么预言,他所做的不过是鼓舞物理学家,让他们相信,之前看似遥远的目标——找到一个简单的数学模式,描述强相互作用粒子的碰撞行为一一终究还是能达到的。
韦内齐亚诺的公式蕴含了被物理学家称为“对偶”的性质:当两个强相互作用粒子相互散射时,可以用两种不同方式计算结果并得到相同结果。在发现这个公式之后的几周里,韦内齐亚诺和几十位同行就开始发展其他对偶模型,希望能描述越来越多的粒子,并研究这种模型与实验学家收集到的新数据是否相符。虽然对偶模型的基础是精确的数学语言,但它们并不能描述实验数据中的细节。不过,许多对偶模型专家都有一种预感,觉得自己一定能发现点儿什么,毕竟这些模型与现代数学的联系是如此紧密。
对偶模型显然和现实世界有关。问题在于,没人知道如何诠释这些枯燥的数学语言,才能帮助物理学家想象出对偶模型描述的粒子。1969年夏天,更为清晰的图景出现了。当时,理论物理学家南部阳一郎(Yoichiro Nambu)、伦纳德·萨斯坎德(Leonard Susskind)和霍尔格·尼尔森(Holger Nielsen)分别独立地使用了几种比喻,比如“长度有限的量子弦”“弹簧”“橡皮筋”“小提琴琴弦”“一维结构”,来阐述对偶模型的数学内容描述的物理现实。不过,物理学家还需要找到一种与量子力学和狭义相对论一致的方式来描述这些微小实体的运动状态。南部率先做到了这点,他在一篇有关对偶模型的会议论文中提到了这种方法。他准备以这篇论文为基础,在1970年8月举办的哥本哈根会议上做一次演讲。不过,事有不巧,在驱车前往机场的路上,他的车在死亡谷内抛错,因此错过了这次丹麦之行。结果就是,这篇论文只是直接分发给了那次会议的与会者,并没有得到广泛传播。因此,直到1972年,“弦论”这个词才成了对偶模型研究者们的日常用语。
弦中幽灵
对偶模型的一大优点在于它们能激发很多新想法,其中的一部分不仅和亚原子粒子有关,还与整个宇宙有关。第一个这样的想法是,时空的维度可能远多于我们大部分人的日常经验。物理学家在试着用与狭义相对论和量子力学一致的方式描述弦运动的过程中遇到了这些更高的维度。问题在于,物理学家每次尝试描述弦运动,最后都会遇到“幽灵态”——在这类状态中,探测到某些粒子的概率可能会低于0。可是负概率完全没有意义。
要想让对偶模型对得起研究它们的那一篇篇论文,就必须把这些幽灵一个一个地清除出去。但是,要怎么做到这点呢? 1969年年末,阿根廷物理学家米格尔·维拉索罗(Miguel Virasoro)观察到了一个似乎值得深究的结果:他证明了对偶模型方程组拥有无限维对称性,且这种对称性来自一种因非凡的数学美而广受赞誉的代数方法。这项进展给理论物理学家带来了一些驱除幽灵的希望,尽管与希望一起到来的还有项令人不安的后果:如果维拉索罗的代数数学方法正确,那么这些模型就必定包含一种只有一个单位自旋的无质量粒子,它和光子很像,却并不完全一样。但根本没有迹象表明这种粒子存在。尽管如此,对偶模型的研究者还是把这种尴尬抛在了一旁,一头扎进了维拉索罗的这种方法。
出生于英国的南非理论物理学家克劳德·洛夫莱斯(Claude Lovelace)在三十五六岁的时候决心要找到一种让对偶模型在数学上自洽的方法,并且想出了一个会产生奇怪结果的方案。1970年,在结束欧洲核子研究组织的工作后,洛夫莱斯在美国新泽西州罗格斯大学谋得了一个职位,他在那儿总以古怪的形象示人,留着长长的花白胡子,就像《圣经》里的先知。他曾短暂地把自己关在普林斯顿假日酒店的一个小房间里,努力寻找一种在数学上自洽的对偶模型建立方法。从身边堆满的书籍和纸张中——其中有很多是现代物理学书籍,还有一些则介绍了庞加莱和黎曼的数学工作——他找到了一种方法可以找出对偶模型要想忠实描述现实世界必须满足的条件。最为重要的是,他提出,要想让对偶模型在强相互作用研究中确有意义,那么时空的维度数量必须是26,一个相当庞大的数字。
物理学家的数学证明
当时,时空可能不止四维的想法已经在物理学世界里流传了将近半个世纪。1919年,柯尼斯堡的德国理论物理学家西奥多·卡鲁扎(Theodor Kaluza)率先提出了这个想法。此后,在哥本哈根工作的瑞典理论物理学家奥斯卡·克莱因(Oskar Klein)又发展了这个概念。"他在1926年提出,空间肯定还有一个维度,只是这个维度因为太小而很难被观测到:这个额外维度中的运动局限在大约只有原子核直径一百亿亿分之一的极微小空间中——远小于实验可观测的最小尺度。爱因斯坦很看重这个想法,但它没有成为主流。与此同时,数学家们越来越习惯处理高维抽象空间。当然,他们并不关心这种高维空间是否与现实有关。
认为四维空间之外还存在一个未被观测到的额外维度已经是个大胆的想法,而认为这样的额外维度还有22个似乎就太过牵强,简直算得上荒唐了。在洛夫莱斯的记忆中,他在普林斯顿高等研究院的一次学术会议上第一次提出这个想法时,就是以“玩笑”的形式呈现的,并且效果很好:“大家都大笑起来。”40年后的2012年,洛夫莱斯在撰写有关自己对偶模型工作的回忆性文章时,仍旧对当年物理同行们对他这个想法的轻视感到痛心。洛夫莱斯在撰写这篇文章时已经78岁了,没有家人,也没有挚友,陪伴他的只有各种奇异鸟儿。写完这篇文章后不久,洛夫莱斯便与世长辞,留下各种长尾小鹦鹉在家中到处飞舞。
如果洛夫莱斯的观点正确,那么在物理学家运用快速发展的高维空间数学方法建立新理论的过程中,多出的这些维度就会带来意想不到的灵活性。在洛夫莱斯公开发表26维空间这个想法之后的几个月内,其他理论物理学家运用这个理论做出了一项令人惊喜的数学发现,让这个理论看上去更加合理了。
在做出这项发现的理论物理学家中,有两位当时正在欧洲核子研究组织的理论部门工作。这个部门位于一座年久失修的实验室大楼内,深藏于廊道之中。1970年,这个研究小组吸纳了几位研究对偶模型的专家。当年9月,彼得·戈达德(Peter Goddard)也加入了这个小组。戈达德时年25岁,却已经有了老派理论物理学家的风范。作为狄拉克方法的忠实拥趸,戈达德更想发展在数学上颇为有趣的宏伟理论,而不是尝试解释实验学家最新得到的令人惊奇的观测结果,大家有时戏称这种行为为“追救护车”。戈达德在这个研究小组中度过了人生中最快乐的时光,组内的氛围令他振奋——开放、乐于合作,并且,正如他后来回忆的那样,他们“以温和的方式”颠覆了正统理论物理学研究方法。
美国理论物理学家查尔斯·索恩(Charles Thorn)在1972年1月加人了这个研究小组,并开始同戈达德合作,希望能证明困扰着对偶模型的幽灵不过是幻象。与此同时,其他几名欧洲理论物理学家和美国同行也在研究这个问题。他们的研究十分重要。如果对偶模型无法摆脱那些幽灵的困扰,那么物理学家只能认为它们毫无意义并无情摒弃。经过数月艰苦卓绝的数学研究,一个春日的午后,戈达德和索恩在准备走进欧洲核子研究组织的自助餐厅时,突然想到了一个答案。戈达德后来告诉我:“我到现在都还记得想出这个答案时我俩所处的确切位置。”他和索恩之前就已明白,如果建立对偶模型的背景不是寻常时空,而是26维时空(没错,就是洛夫莱斯提出的时空维数),那么这类模型就不会受到那些幽灵的困扰。
戈达德和索恩证明一一麻省理工学院的理论物理学家理查德·布劳尔(Richard Brower)也做到了这点一一有一个定理可以保证对偶模型中不会出现那些幽灵,这个定理就叫作“无幽灵定理”(no-ghost theorem)。虽然他俩把这个结果发表在了《物理快报》(Physics Letters)上,但大多数读者还是把这篇论文归为高等数学方面的内容,事实也是如此。然而,如果对偶模型的确能可靠地描述自然世界,那么这些高等数学必须正确。这个结果完全出乎纯数学家的意料。他们一直觉得物理学家太马虎,不可能想出这么严密的定理。然而,事实摆在眼前,物理学家就是证明了这么一个严密的数学定理,而且它看上去和现实世界完全不沾边。戈达德后来回忆说:“无幽灵定理对我产生了深远影响。它的证明展示了一个优美的数学结构,而且是纯数学家此前无法企及的优美结构。”物理学抛出了一个连数学家都不知道自己需要的数学证明。戈达德相信,对偶模型涉及的数学内容一定有些神奇的地方,并且认为,即便这类模型“取得成功的概率微乎其微”,也“值得好好研究”。
友好的巨人
20世纪70年代,纯数学领域各分支的一些艰深的前沿问题常常通过对偶模型与物理学联系在一起,这令戈达德颇为惊讶。他最感兴趣的一个例子与群论(研究对称性的数学分支)的一些怪异发现有关。而且,这些发现最终正是通过戈达德等物理学家发展的方法才得以解释。这个故事始于20世纪60年代末的剑桥大学。当时,戈达德还是那儿的理论物理学研究生,无意间听到数学系的朋友们讨论有关对称性的新研究。爱好广泛的数学家约翰·康威(John Horton Conway)正和同事们尝试给离散对称(对某个具有对称性的数学对象进行离散变换而使该对象保持不变的方法)的所有基本构件分类。康威猜测,24维空间中的一种特殊对象所具有的对称性就是这样的一种基本构件。他还证明了,这种对象具有的对称性总数超过800亿亿。
几年后,德国人伯恩特·菲舍尔(Bernt Fischer) 和美国人罗伯特·格赖斯(Robert Greiss)推断,还有一种拥有更多对称性的更大的基本构件。准确来说,它所具有的对称性数量是808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000。这个基本构件存在于——或者更精确一点儿说,作用于——196 883 维空间中。格赖斯称这个基本构件为“友好的巨人”(Friendly Giant),这个绰号来自很受欢迎的同名加拿大儿童电视节目,而且这个名字的两个单词的首字母正好与菲舍尔和格赖斯姓氏的首字母一样。不过,这个基本构件更为人所熟知的名称却是康威起的“魔群”(Monster Group)后来,数学家又证明这个魔群的性质极其古怪离奇,康威就改称它为“魔群月光”(monstrous moonshine)。
直到1981年夏天,魔群才得到严谨的证明,通过考验成为正规数学的一部分。弗里曼·戴森听到这个消息后,激动得忍不住做了一个异常疯狂的猜测:“21世纪的某个时刻,物理学家会突然发现魔群以一种前所未有的方式根植于宇宙的结构中。”10年后,戴森的这个猜测看起来好像不那么疯狂了。英国数学家理查德·博彻兹(Richard Borcherds)用卓越的数学技巧证明了“月光猜想”。对偶模型专家比数学家更熟悉博彻兹在证明过程中用到的方法。在证明“魔群月光”特性的过程中,博彻兹大量使用了对偶模型涉及的数学内容,其中包括戈达德和索恩的“无幽灵定理”。
无幽灵定理对数学与物理学关系的重要性仍不明确。或许,这个定理只是对偶模型在粗略描述亚原子世界的过程中产生的一种颇受欢迎的数学副产品。这个定理会不会像一个世纪前从以太模型中兴起的扭结理论那样随后被证伪?又或者,无幽灵定理的成功会不会成为 275年前莱布尼茨发现的数学和物理学之间存在“预设和谐”的又一个例子?
超对称
对偶模型的另一个产物是超对称。这个概念之前没有任何人想到过,但许多物理学家开始相信,超对称可以应用于自然世界的所有基本方程组。如果这种对称性真的能应用于现实世界,那么它就会给我们对时空的认识带来自爱因斯坦提出相对论之后最具革命意义的改变。
超对称的故事可以追溯到20世纪20年代。当时,量子力学的先驱做出了一项令人惊讶的发现: 每种原子尺度粒子的行为都与它的自旋存在至关重要的关联。例如,光子(每个光子的自旋都为1)的行为就与电子(自旋为1/2)不同,这是实验学家们反复验证过的事实。事实证明,原子尺度的粒子可以分为两类。一类是自旋为0,1,2,3等整数的粒子,叫作“玻色子”: 另一类是自旋为 1/2,3/2,5/2 等半整数的粒子,叫作“费米子”。玻色子和费米子的性质不同,这就引出了一个显而易见的问题:这两大类粒子可以用一种对称性来描述吗?
第一批对偶模型,包括韦内齐亚诺的在内,都有局限性,因为它们只适用于玻色子。怎么才能把它们拓展到费米子呢?在尝试回答这个问题的过程中,理论物理学家发现了超对称。有了这种全新的对称性他们就能用一个理论框架描述玻色子和费米子。和许多伟大的科学思想一样,超对称的概念并不是某个人一时灵光乍现的产物。其中的一条线索来自1970年圣诞节前不久芝加哥附近的费米粒子加速器实验室中。在这个实验室的理论部门中,出生于法国的年轻理论物理学家皮埃尔·雷蒙德(Pierre Ramond)——当时他刚刚拿到博士学位——兴奋地发现了一种将对偶模型拓展至费米子的方法。他后来告诉我,他是用电子的狄拉克方程“同已经建立的对偶模型做类比,以图建立一个同时适用于玻色子和费米子的模型”时有了这个想法的。雷蒙德证明,狄拉克方程蕴含着一种新对称性的种子。他还证明,狄拉克方程可以从对粒子的描述推广到对弦的描述,而描述弦的方程组就蕴含着超对称。大约和雷蒙德同时,理论物理学家安德烈·内沃(Andre Neveu)和约翰·施瓦茨(John Schwarz)也独立提出了类似的想法。
1973年秋天,超对称离应用于现实世界又近了一步。当时,卡尔斯鲁厄大学的尤利乌斯·韦斯(Julius Wess)和欧洲核子研究组织的布鲁诺·朱米诺(Bruno Zumino)将这个想法应用到了四维时空中。如果现实世界的确有这种对称性,那么粒子物理学标准模型就必须拓展。按照超对称的要求,一个不可避免的后果就是,自然世界中存在的粒子种类要比之前人们认为的更多。这是因为超对称要求标准模型中的每种粒子都有对应的新粒子,后者被称为“超粒子”(sparticle)。在超对称标准模型中,轻子和夸克家族的每一个成员(都是费米子)都有对应的玻色子粒子;同样,每一种规范粒子(都是玻色子)也都有对应的费米子粒子。例如,自旋为 1/2 的电子和夸克都有自旋为0的对应超粒子分别被称为标量电子和标量夸克。同样,自旋为1的光子和胶子也有自旋为1/2的对应超粒子,分别被称为光微子(photino)和胶微子(gluinos)。难怪人们嘲笑超对称术语为“超语言”。
要想探测到这些假定的超粒子并不是一件容易的事。物理学家面对的问题在于,对称性几乎没有给出任何有关超粒子质量的信息,因此,实验学家根本不清楚去哪里捕获它们。这就意味着,当物理学家为了在前所未有的高能量下研究粒子相互作用而建造新加速器时,没人可以确定超粒子会出现。
超对称成为物理学家宠儿的一大主要原因在于——暂且不论检验它的技术条件是否已经成熟一一它并不是传统意义上的数学对称性:超对称独一无二。要将时空对称性(由爱因斯坦狭义相对论描述)拓展到量子世界,超对称是唯一有可能成功的方法。在这个修正版的时空中,表征“空间”每个方向上“长度”的不再是可以从测量仪器上读取的寻常数字了,而是被称为量子算符的抽象数学对象。这意味着,超对称描述的量子时空概念与我们日常经验中可以用尺子和钟表测量的时空大相径庭。这又一次证明理论物理学家在用新思路思考亚原子世界的过程中有时会产生新的世界观一一当然,最为重要的是,这种思考是在数学的辅助下展开的。
超对称的独特性还体现在另一个方面。只有整合了超对称,大自然才能赋予基本粒子所有可能的自旋:如果超对称只是理论物理学家集体虚构出来的产物,那么大自然就会错过至少一种基本粒子,也就是自旋在0~2之间的粒子,而它们是狭义相对论和量子力学允许出现的。
用更通俗的语言来说,超对称的作用就像一种魔力符咒,有了它物理学家就能运用标准模型做一些非常麻烦的计算,比如粗略估计希格斯粒子的质量。在许多支持超对称的科学家眼中,超对称太美了,因此绝对不可能是错的——大自然要是不利用这种性质,那真是太不可思议了。
然而,目前还没有任何实验证明超对称的存在,并且有一些理论物理学家,包括美国的几位顶尖学者在内,并不相信超对称在大自然的规划之内。例如格拉肖(Sheldon Lee Glashow)后来就对我说:“在欧洲,超对称似乎成了一种宗教。”如果把超对称看作一种宗教,那肯定出现了一些叛教者,其中最出名的应该是杰拉德·特胡夫特(Gerard 't Hooft),他对我说:“我没看到大自然给物理学留的位子中有超对称的一席之地,所以我对这个概念还是敬而远之比较好。”
超对称不只是理论物理学家的福音,对纯数学家来说也是如此。可以想见,第一个证明这种新的自然对称性在当代数学中也有威力的就是物理学家爱德华·威滕(Edward Witten)。1981年夏天,他在科罗拉多州阿斯彭的一个游泳池里突然有了一个想法。那个时候,威滕已经成了理论物理学界公认的超级天才。虽然威滕平日里不怎么说话,但当他对某些技巧特别有感觉时,他的语速就会变得很快,并且毫不犹豫、没有偏差、绝不重复,就像是在念预先写好的稿子一样。威滕显然很欣赏自己的精湛技巧:我还记得有一次看到他在结束讲座时春风满面的样子,那个笑容很像几十年后罗杰·费德勒用胯下击球赢下一分后的表情。
在游泳池里,威滕凭直觉想到,超对称可能与数学中的莫尔斯理论有关。莫尔斯理论主要研究的是数学函数与其描述的空间形状之间的关系,以美国数学家马斯顿·莫尔斯(Marston Morse)的名字命名。50多年前,莫尔斯率先提出了这个理论的许多主要思想。很久以前,麦克斯韦也发现了这个理论的许多元素。在利物浦刑事法庭举办的1870年英国科学促进会年会上,麦克斯韦做了题为“小丘和山谷”的演讲,并在演讲中第一次公开讨论了他的这些发现。在那个周六上午举办、到场人数不多的讲座中,麦克斯韦解释了数学推理在研究乡村地貌特征时提供的独特视角。后来,有几位听众反馈说,麦克斯韦能把一个听上去如此简单的课题翻译成许多人都多少有些恐惧的数学语言,这令他们大吃一惊。
不过,参与这次讲座的几位专家却有幸看到了麦克斯韦这位自然哲学家开创了一个新数学分支,也就是后来人们知道的莫尔斯理论。一个世纪后,这个理论成为数学界一个比较热门的理论。在科西嘉岛上举办的一期暑期课程中,威滕第一次听说了这个理论。当时,能力过人的数学家拉乌尔·博特(Raoul Bott)在开始讲课前对听众说,他接下来要介绍的这个理论是自己最喜爱的一个理论,并且未来有一天或许会对台下的各位有所帮助。威滕一直都觉得这个理论和现实世界没有什么关系,直到他在游泳池中灵光一闪。几年后,他在莫尔斯理论和超对称之间建立了完全意想不到的联系。
拓扑学家们都十分震惊。他们很难相信一个大多数数学家知之甚少甚至一无所知,且未经证实的物理学理论,竟然可以给对高维抽象空间形状的研究带来全新的视角。毕竟,这个领域似乎怎么看都和现实世界没有任何关系。威滕的一大洞见是,整合了超对称的改良版量子力学方程组与50多年前几何学家威廉·霍奇【William Hodge,迈克尔·阿蒂亚(Michael Francis Atiyah)的研究生导师】发现的方程组一模一样。也就是说,物理学家又一次踏上了数学家在几十年前铺设好的道路。狄拉克在1939年的斯科特讲座上评论道:“数学家觉得有趣的规则正是大自然选用的规则。”此时这番评论比以往任何时候都更能引起共鸣。
威滕在职业生涯初期对过多强调物理学与数学之间的关系持谨慎的态度。他后来回忆说,自己“只是逐渐”看到了向数学家学习带来的好处。他在20世纪70年代中期偶然发现量子场论和现代数学交汇时,只觉得那是一种“例外”,一种难得一见的奇怪现象。不过,到了20世纪80年代初,威滕越发相信前沿数学可以不断地促进前沿物理学的发展,反之亦然。
20世纪80年代中期,我察觉到许多具有数学头脑的理论物理学家认为,超对称在数学领域的成功至少间接证明了这种对称性是大自然的一种根本特征。当时,我常常听到理论物理学家对会议听众说,现在的问题并不是超对称是否能够得到证实,而是何时能得到证实——超对称预言的“新”粒子早晚会出现。
不过,这样的夸张说法并不能打动大部分实验学家,比如直率的意大利人卡洛·鲁比亚(Carlo Rubbia)。1986年,在一次理论物理学家和实验学家都参加的会议上,他直言不讳地说:“我感觉自己就像这场理论狂欢中的濒危物种。我真的很惊讶。理论学家们发明了一个接一个的粒子。现在好了,每一种已发现的粒子都有对应的未发现粒子,而找到它们的重任当然应该落到我们实验学家身上。我觉得自己就像住在一幢烂尾楼里,墙壁只有一半,地板也只有一半……理论物理学界看待物理学的方式和楼下实验学界眼中的真正情况大相径庭。”
结果,所有物理学家一致同意,确定超对称是否适用于现实世界的唯一方式就是让宇宙通过实验结果来告诉我们。同往常一样,吹嘘自己完全了解新理论价值的物理学家总是面临着被大自然狠狠打脸的风险。
弦论的缺陷
1974年,在加布里埃尔·韦内齐亚诺偶然间提出第一个对偶模型的6年后,物理学家开始意识到他们诠释这个模型的方法并不正确:这个模型并不仅仅适用于强相互作用力,而是适用于所有自然基本力,包括引力。换句话说,弦论的研究对象并不局限于原子核内部,而是包含了整个物质世界。
弦论适用于所有基本力的想法首先出现于两位顶尖对偶模型研究专家——美国人约翰·施瓦茨(John Schwarz)和法国人若埃尔·舍尔克(Joël Scherk)撰写的一篇文章中。他们用极其冷静的语言——几乎没有展露自己的兴奋之情——解释说,把超对称包括在内的传统弦论,如果采用这种全新的诠释方式,就可能成为在最精细层面上全面描述自然世界的统一理论的基础,而这种统一理论正是理论物理学家一个多世纪以来梦寐以求的。
弦论的核心是描述自然世界最深层面的具有革命意义的全新图景它表明,电子、夸克、光子以及其他所有实验学家已经探测到的所谓基本粒子其实并不基本。如果弦论正确,那么就只有一种真正的基本实体,也就是弦:粒子只是弦振动的产物,就像拉动小提琴琴弦时产生的音符一样。物质宇宙其实就是弦上奏出的音乐。
这种方法以精确的数学为框架,似乎很有效。最令人印象深刻的是,弦论的形式天然就包含引力,而这是此前那些描述亚原子力的场理论做不到的。弦论只在引力同其他基本力一道存在时才有意义。换句话说,弦论本身就表明了引力的存在。这个理论的另一大优点在于,它不包含把爱因斯坦引力理论同量子力学结合在一起时突然出现的无穷大量。事实证明,这些无穷大量在弦论中奇迹般地消失了,因此,它在数学上是有意义的,这点令大多数专家都感到惊喜。
然而,弦论也有一些令人忧心的缺点。它在技术上的一大明显缺陷在于,它的数学结构似乎表明,这个理论与“左右”对称性破缺似乎并不相容,而这种破缺在李政道和杨振宁预言后,已被实验学家在 20世纪50年代中期证实。如果理论物理学家不能修复这个问题,那么弦论就完了。
另一大重要缺陷在于,弦论似乎并不能被实验验证,至少在可预见的未来不行。自牛顿的研究方法成为物质科学研究的基本方法以来,在将近250年的时间里,任何提出新科学理论的人都应该做出实验学家可以检验的预言。然而,就弦论来说,这种检验并不可行,因为只有将它应用于大爆炸的最初时刻,也就是时间本身开始的那一刻,极高能粒子的相互作用时,弦论才能做出清晰的预言。在这种能量(也就是“普朗克能量”)上下,物理学家用来描述日常世界的物理量,比如长度、时间、质量,都开始失去自己的固有含义,而物理学定律也就失效了。
在这种能量水平上,量子理论和狭义相对论需要共同描述自然力或许弦论的框架可以帮助它们做到这一点。问题在于,没人知道在现代粒子加速器所能产生的这种相对低的能量水平下,如何运用弦论做出详细的预测。除非实验学家能够验证弦论物理学家的预言,帮他们悬崖勒马,否则他们就有可能坠入纯思想的深渊,也就是虽然有高等数学的优雅描述,但它和现实世界仍然毫无瓜葛。
1974年春天,施瓦茨和舍尔克很是兴奋,因为弦论可能是统一场理论的圣杯。他们在全球大学的物理系和物理学会议上做讲座,听众总是会礼貌性地倾听,哪怕他们其实无动于衷。当时,大多数粒子物理学家并不觉得研究引力是自己工作的一部分,而大多数引力专家则对亚原子物理学知之甚少。
舍尔克和施瓦茨认为弦论适用于所有自然力的观点正式发表于1974年10 月,“11月革命”的3周之前。对那些胸怀大志的粒子物理学家来说,规范理论仍是唯一的研究对象——现在可不是研究推测性理论的好时候,无论它看上去多么有前景。在当时看来,最好的研究策略就是在新实验结果的指引下发展标准模型。
研究弦论的圈子一直都很小,11月革命后,这个圈子就更小了。物理学家通常都更看重那些能在规范理论和实验数据之间建立联系的机会,也有人如前文介绍过的那样,侧重于发展理论背后的数学内容。施瓦茨和舍尔克是少数几个信奉弦论的物理学家,且后者于1980年离世年仅33 岁。施瓦茨则在加州理工学院继续研究弦论,主要合作伙伴是迈克尔·格林(Michael Green)。这两人此前在欧洲核子研究组织的自助餐厅吃午餐时偶遇,之后便迅速重拾了 10年前于普林斯顿初见时的友谊。格林在伦敦大学拥有讲师的永久职位,而施瓦茨则为选择研究冷门课题付出了代价——虽然他是加州理工学院第一流的物理学家,但他并没有终身职位。
“那些日子里,”理论物理学家杰夫·哈维 (Jeff Harvey) 如今回忆道,“格林和施瓦茨真的身处荒郊野外。”他们研究的是整合了超对称的弦论,或者说“超弦理论”,它能够将弦论描述的时空维数从26降至更容易让人接受的10,但这个理论离主流物理学的研究课题仍旧很远。即便是那时,施瓦茨研究10维空间的行为也没有得到大多数加州理工同事的理解,其中包括持怀疑态度的理查德·费曼,后者曾在走廊里开玩笑地大喊:“嘿,施瓦茨,你今天研究几个维度啊?”
虽然施瓦茨等人在弦论领域确实取得了一些进展,但他们说服不了多少理论物理学家加入,即便是那些最具数学头脑的也不行。施瓦茨后来回忆说:“大家对这个领域仍旧毫无反应。”威滕倒是为弦论做出了一些贡献,但这个理论的缺陷之深令他担忧,因此,他并不愿意全身心地投入进来。威滕担心,弦论可能成为一项战线极长的长期挑战。不过,1984年秋天,在读完一篇改变了物理学进程(某种程度上也改变了数学进程)的论文后,威滕对待弦论的态度发生了大幅转变。

本文经授权摘自《物理世界的数学奇迹》(中信出版社,2020年7月)第八章《弦论,魔法还是玩笑?》,小标题为编者所加,有删减。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 