文章通过实例讨论物理学理论与实验的“非常”关系，理论物理在追求“唯美”的同时如何“求真”；阐述是不是只有被“证实”了的理论才能是“有用的”，究竟什么样的实验才算验证理论物理的预言。作者还通过自己过去 20 年关于介观统计热力学的研究工作的历程，展示如何在开展理论物理引领的基础研究的同时，兼顾真正的应用需求。

撰文 | 孙昌璞

国家自然科学基金理论物理专款（下称“专款”）设立已经 30 周年了，作为前七届“专款”学术领导小组的成员（1993～2022 年）和第七届“专款”学术领导小组的组长，我亲历“专款”在不同的历史时期如何推动我国理论物理学科的建设和发展，也见证了彭桓武等老一辈理论物理学家为促进我国理论物理事业的进步，严谨认真，殚精竭虑、心系全局、以长远的眼光务实当下、布局未来。

在“专款”工作中，本人有幸聆听了老一辈的教诲，在耳濡目染中不断学习他们的思想方法和工作作风。很早有机会参与“专款”对我国理论物理的组织领导工作，使我得以从不同的视角全面地了解理论物理的发展[1, 2]。同时，自己也积极在科学研究前沿进行着不懈的探索，通过研究工作的积累，对当代理论物理趋势和我国理论物理发展前景形成了一些个人的浅见。文章将围绕着理论物理“唯美”与“求真”的核心价值观，强调理论物理具有基础性和综合交叉性的根本特征。从科学方法论（哲学）的角度，通过实例讨论了理论与实验的“非常”关系，明晰了“实验证实理论”的科学哲学内涵，并阐述为什么基本物理的理论工作在一段时间内可以与即时的实验验证保持距离。本文强调要做“有用”的理论物理——应用理论物理，并指出需求驱动的科学研究与自由探索一样，也会导致实现基础物理的重要突破。最后，通过我们过去 20 年关于介观统计热力学的研究工作的历程，展示如何在开展理论物理引领的基础研究的同时，兼顾真正的应用需求。

本文的部分观点引述了笔者为《物理学报》“观点和展望”撰写的文章《当代理论物理发展趋势之我见——杨振宁学术思想启发的若干思考》[3]。

01理论物理为什么比物理理论更重要？

理论物理作为物理学的基础分支学科常常被人们质疑：既然物理学不同的学科分支有各自的物理理论，为什么还需要有理论物理这样的学科？理论物理典型的学科特征是什么？历史上关于发展物理理论还是理论物理在我国曾经有过一些学术争论。在不同的历史时期，这种争论有时还不仅仅停留在学术层面上。在“理论脱离实际”大帽子下，那时有的科研院所曾多次解散理论物理研究室。即使在当下，抽象的理论物理工作也会被质疑：为什么还没有被实验所“证实”？或理论物理的研究成果有用吗？本文不奢望能够完美回答这些质问，而是要尽最大努力阐释问题更底层的逻辑：“实验证实理论”的内涵究竟是什么？是不是只有被“证实”了的理论才能是“有用的”？

众所周知，物理学通常是基于“还原论”（reductionism）和“演生论”（emergentism）两种科学范式来描述物质世界运动和构型的。前者把物质性质归结为最基础组元间的基本相互作用——电、弱、强相互作用和引力[4-6]；而后者主要研究多粒子组成的复杂系统，把较高的结构层次“演生”出来的有序和合作效应的规律当成基本定律加以探索[7, 8]。两种理论范式采取的共性科学手段是利用实验进行主动的观测，理论物理通过建立理论模型、经过哲学性思考，提出初步的科学理论假设，然后借助新的实验进行判定性的检验，最后用严格的数学语言精确、定量地表达其中一般的科学规律——物理定律，由此再进一步预言新的物理效应，并把其中的普适的规律应用到新的领域。理论物理学的这种研究方法，决定了其作为一门独立学科存在的必要性，也预示着它在物质科学研究中具有不可或缺的核心地位。

在中文语境中，王竹溪和郝柏林曾经明确定义了什么是理论物理：“理论物理是物理学的一个分支。理论物理学把物理学各个分支领域对物质运动规律的研究成果作出高度概括，表述为基本的定量的关系，建立起统一的深刻的理论体系，说明和预见新的物理现象。许多实验和理论的集体，既分工又配合，在理性认识和感性认识的多次循环往复中，使物理研究工作步步深入，揭示和应用自然界的客观规律……”[9]他们还进一步强调，“一方面，物理学的各个分支都有相应的理论，另一方面贯穿于各个方面的理论又形成体系，构成理论物理学科。理论物理又起到沟通各个分支学科的桥梁作用”。由此看来，理论物理学是一门跨越物理学各个分支领域乃至其他物质科学领域的综合交叉学科，它的基本性和普适性意味着它比零零散散、针对具体的物理理论更为重要！

围绕着“还原论”和“演生论”的世界观，物理学形成了各自不同的学科分支。前者有粒子物理、核物理和原子分子物理等，而后者包含凝聚态物理、等离子体物理和激光物理等。物理学的理论基础是“四大力学”，但它们又各自发展出新的理论，如激光理论、固体理论等。两大方面的诸多学科的共性问题和普适规律可以通过理论物理有机地联系起来。因此理论物理在内涵上具有本质交叉的明显特征，通过数学和模型把物理学的各个分支的理论相干地融合成一个理论总体。

凝聚态物理学形成当代物理学最大的分支，它把量子力学和统计物理成功地运用到固体和液体等凝聚态系统中，奠定了材料、信息、生物科学和能源技术的科学基础。反过来，基于凝聚态发展起来的相互作用多体理论对整个物理也有基础性的贡献：从凝聚态物理的研究中凝练出来的普适思考和方法，对包括高能物理在内的其他物理学科的发展也起到根本性的作用。如大家所知，要满足局域规范对称性的要求，原初的杨-Mills 规范场是没有质量的，这使得规范场理论多年不能有实际应用。后来，南部（Yoichiro Nambu）把BCS 超导理论中蕴含的对称自发破缺机制应用到基本粒子物理，通过 Higgs-Anderson 机制使得规范场获得质量，由此建立了杨-Mills 规范场论描述的电弱统一标准模型和关于强相互作用的量子色动力学（QCD）。对称性自发破缺机制的发现作为物理学发展历史上的一个重要里程碑，已经成为当代理论物理必不可少的基础性内容。需要指出的是，对称自发破缺机制提出之后，在彭罗斯（O. Penrose） 和昂萨格（Onsager）工作基础上，杨振宁发展起来的非对角长程序（off-diagonal long range order，ODLRO）理论与对称性自发破缺机制是等价的，是对超导和超流等演生现象更严格的理论描述。可以说，Higgs-Anderson 机制是理论物理中“还原论”和“演生论” 和谐统一的光辉典范。

02为什么理论物理是物理学最唯美的分支？

物理学的目标是研究物质世界的结构和运动规律，但实际物质世界极为复杂多样，导致了研究方法和手段也百花齐放，名目繁多，在技术层面上难以统一起来。从科学思想的角度看，基于“还原论”和“演生论”物理学的不同分支领域也会有价值观上的差异。相应地，从实验的角度看，高能粒子物理基于“还原论”的代价是需要昂贵的大型科学装置，因此高能粒子物理验证理论预言的时间要久远一些，如 Higgs 机制的证实用了 50 多年。因此，判断一个基于“还原论”的物理理论的“好坏”，并不能仅仅依据是否能被即时验证。基于“演生论”的凝聚态物理等学科，较为贴近日常生活，大多采用相对经济、短时间内可实现的桌面实验系统进行验证。因此，就整个物理学而言，理论能否“马上被证实”在短时间内不应当被当作理论工作好坏的判断标准。

判断一个理论好坏的价值观是多元化的，在物理学内部自然也会带来一定程度上价值观的冲突。凝聚态物理学家安德森（Philip Anderson）不断强化“多者异也”（more is different）的“演生”观点，已经以某种方式影响了美国超导超级对撞机（SSC）建设的下马，当年温伯格（Steven Weinberg）与他有过激烈的公开争论。从事高能理论研究的人经常会把有诸多条件不明近似和假设的凝聚态理论视为“脏物理”（dirty physics）。诚然，多元化的价值观是理论物理学发展的活力所在，但由此引发的分歧有时也会影响物理学的和谐发展[9]。这不仅仅是因为资源的约束，更多的是由于思想方法的差异。现在的问题是，是否存在一种共同的内在价值的选择突破这种多元价值冲突的困境呢？爱因斯坦（ Einstein ）、玻尔兹曼（Ludwig Boltzmann）、狄拉克（Dirac）、杨振宁和巴丁（Bardeen）等理论物理学家通过自己具体的科学实践找到了统一其多元化价值观的途径，那就是在求真过程中，共同的目标是追求科学之“美”[10, 11]。

“美”看上去是主观的东西，它怎么可以作为以实验为基础的理论物理学的价值标准呢？对此，杨振宁复述了玻尔兹曼的观点：物理理论有美妙的地方，每一位物理学家对这种美妙有不同感受， 形成自己的风格。这种不同的感受就是杨先生所说的“taste”（品味）：有了对科学之“美”的追求，狄拉克可以不惧玻尔、海森伯和泡利等权威，在“数学之美”的思想境界写下狄拉克方程，神奇地预言了反物质的新世界。杨振宁也正是在这类“美”的价值观驱动下，基于对称性的考虑，和 Mills 一道，大胆地提出了杨-Mills 规范场论，而不“介意”泡利基于当时规范场尚无质量这一事实的多次质疑。

当然，大而化之地谈“品味”和“风格”，并不能告诉大家“美”为什么能够作为判断理论好坏的标准。经过多少年的科研实践和一些哲学思考，我体会到其基本原因可能源于数学“唯美”的价值观。当年和我同时在美国长岛纽约州立大学石溪分校访问的王元先生告诉我，好的数学和艺术一样，美学是第一标准，数学美在于大道至简[12]：“理当则简，品贵则简。”数学美不是人造的，它亘古有之、天道自然，这也是与人为创造的艺术之美的本质分野。物理理论之美在于自然物质有其结构之美，而描述它的理论框架必有数学之美。它赋予了（物理）科学之美以客观的属性，自然不同于难以言说的艺术之美。数学美和物理学美有同根的地方，也有差别。杨振宁对数学家在不知道物理背景的情况下独立地发明了“规范场”−纤维丛上的联络一事感到惊讶，认为数学家“凭空梦想出了这些概念”。但数学大师陈省身先生却认为“它们是自然的，也是实在的”。因此，虽然数学和物理学关系密切，但它们各有各的价值观和文化传统，“有着不同的发展方向”[13, 14]。

数学不仅用“美”统一了理论物理的多元价值，而且要为理论物理学发展提供更严谨的分析及推理手段，后者导致了传统的数学物理的诞生和发展；反过来，理论物理学的新需求也牵引了数学的新发展，由此引申出来的概念和方法也启发了新的数学思想和数学分支的诞生，这也是今后理论物理发展的新趋势——现代数学物理。这些新的发展当然是“唯美”的，甚至可以暂时不计物理应用的实用目标的。可以说，这个发展趋势主要是由爱因斯坦、狄拉克发起的。在 20 世纪六七十年代后， 由杨振宁和威滕（Edward Witten）等人先后把它推向了一个新的高潮：狄拉克给出的关于量子力学的 q 数-c 数理论，导致算子代数的诞生；引入了 δ 函数，导致了广义函数理论的建立。作为对数学学科拓展也深具实质性影响力的理论物理学家，杨振宁秉承了狄拉克“唯美”的学术精神，深刻理解物理学美与数学美的关系。他建立的规范场理论和杨-Baxter 方程实质上推动了两个新的数学分支发展，即 Hopf 代数−量子群和四维可微流形分类。他的这些工作深刻地影响了 20 世纪 80 年代中国数学物理的发展，如推动经典规范场与磁单极、可积系统与量子群的研究，培养和锻炼了几代在数学物理领域有国际影响的理论物理学家。

03什么样的实验才算验证了理论物理的预言？

物理学本身是一门基于实验求“真”的科学。作为物理学的一个学科分支，理论物理的“真理性”必须经受实验的考验。然而， 理论物理不仅仅要面对各种具体的实验，而且要立足于足够多的实验总和之上并发现共性规律。因而，其阶段性的理论研究，有的开始可能看不到实验检验的可能，但经过进一步拓展和改进却可以导致重大突破和科学革命——广义相对论和规范场论是这方面的典型例证。鉴于这种事实，我们可以追问：理论物理的“真”是不是要求马上有实验验证？是否要仔细考量实验是不是“真”的验证了我们要验证的东西？从科学哲学的角度甚至还可以进一步地追问， 理论本身能够被证实吗[15]？笔者可以举几个例子来说明这些追问并非平庸和形而上学。

有时，判断实验是否“真”的验证了理论十分困难。当实验物理学家知道了“理论”的预言结果，处理实验数据就会有主观的倾向，“实验验证了理论”的断言就不那么令人信服了。这里可能会出现科学研究的“灰色地带”，也可能出现严重的科学诚信问题。1956 年，李政道、杨振宁发现宇称不守恒并建立中微子二分量，预言 μ 子到正负电子衰变的实验分支比是 3/4。此前实验发现分支比在一定范围内几乎是随机的，而此后 10 年里，不同研究组进行了多次实验，最后分支比的测量值都稳定逼近 3/4（图 1），其中每一次实验的误差（error bar）都落在前一个实验误差里边[16]。这个事例告诉大家，单次实验观察不到“真”、不可能完全独立于理论去无偏地验证理论预言。因此，仅凭一次和少数几次实验检验理论正确性是不可靠的，只有多次重复实验才能逼近理论描述的“真”、发现物质世界的“真”与“美”。

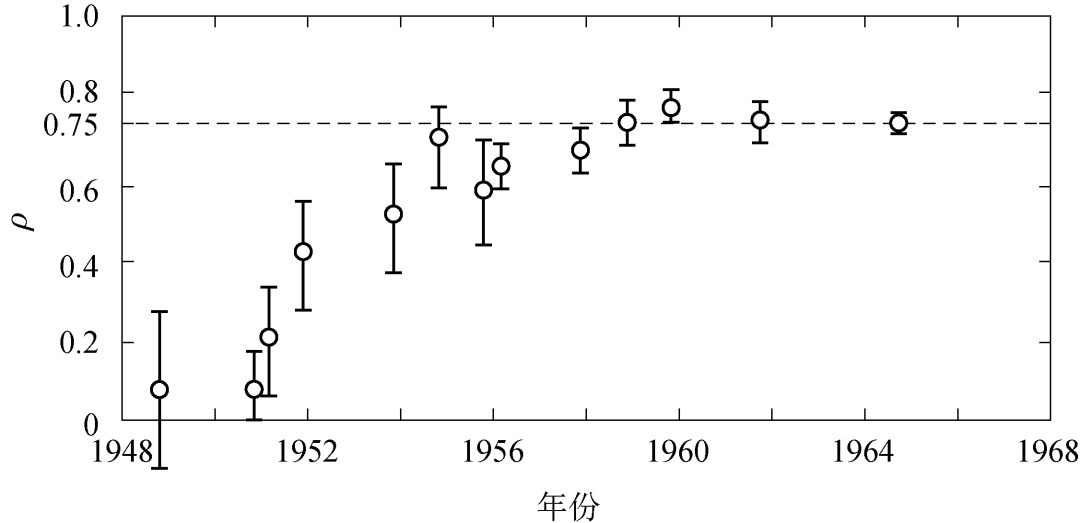
图 1. 1957 年李−杨的理论预言影响了测量 μ 子到正负电子衰变的分支比的误差处理：测量每一次实验的中值都落在前一次实验误差范围内，10 年后逼近预言 3/4 而趋于稳定。

其实，实验物理学家看到的“理论”预言有可能只是在十分苛刻条件下的某种简化模型和低阶近似的结果，这就是最近马约拉纳（Majorana）零模实验的问题所在。在一定条件下，超导−纳米线（拓扑绝缘体）紧邻复合系统理论上一定会约化到 Kitaev 模型[17]， 它的激发谱就会出现 Majorana 零模。然而，在实际的强场（或强表面能隙）条件下，它们并不能约化到理想 Kitaev 模型。这时，即使观察到的零偏压信号，也不能代表 Majorana 零模。
 

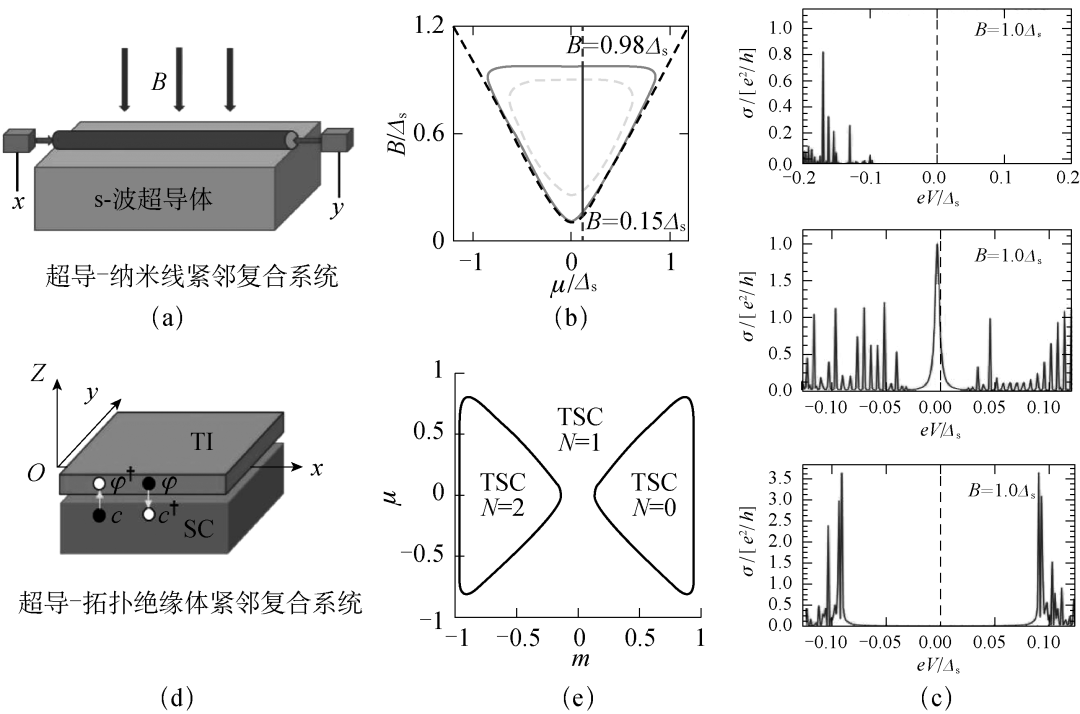
图 2. 实际紧邻系统及其相图与关于 Majorana 零模实验观察。左：超导−纳米线实际系统（a） 和超导−拓扑绝缘体实际系统（d）；中：更严格方法预言的相图——纳米线体系相图随磁场变化由开到闭（b），拓扑绝缘体系统相图表面能隙变化由开到闭（e）；右：超导−纳米线系统微分电流随磁场变化的严格计算（c）。磁场超过一定强度，Majorana 模的效应消逝。

我们最近的研究表明[17]，对于超导−纳米线紧邻复合系统（图2（a）），在化学势 μ−磁场 B 平面上，磁场很弱时，“理想拓扑相图”边界是开口向上的类抛物线。这时，通过紧邻效应，超导线中的虚激发在纳米线上诱导出电子配对，近似理论预言的配对强度不依赖磁场。然而，仔细进行更精确的解析分析或严格从头计算就会发现，有效配对强度一定依赖于磁场，它使得“相图”边界变得封闭。当磁场强度超过“相图”边界顶部，拓扑相变就不会发生，因此不会有 Majorana 激发（图 2（b），（c））。对于超导−拓扑绝缘体紧邻复合系统（图 2（d））也存在同样的问题。在配对强度 Δ−表面能隙 m 平面上，期望约化到的理想 Kitaev 模型给出的拓扑边界是直的，拓扑区域对能隙 m 的取值并没有上限要求。然而，通过更严格的计算可以发现，有效配对强度会依赖于表面能隙 m，它也使得“拓扑相图”边界变形并封闭（图 2（e））。当表面能隙超过超导能隙 Δs 时，拓扑相已无严格定义，也就没有很好定义的 Majorana 模（ 图 2 （ e ））。与纳米线体系实验一样， 基于拓扑绝缘体系统的Majorana 实验，也没有达到理论拓扑相变的条件。对于上述两种复合系统用来模拟 Kitaev 模型，实验家相信最低阶近似下有效模型理论的预言，却不符合他们的实验条件。为此，有人有取向地处理数据（或干脆不采用自己观测到的数据），得到看似与近似理论相符合的结论。不过最终，这些应合低阶近似有效理论的 Majorana 实验的大量文章被撤稿了。

笔者认为，上述问题产生的深层次根源在于这个领域中的一些人不能正确地理解、处理理论和实验的关系，有意无意地把近似的有效模型当作实际系统来研究，忽略了理论预言成立的条件；他们不仅在得到实验上的结论时人为地迎合“理论”，而且在阐述其重要性时也过分地依赖于“理论”，不能客观地使用实验数据——为了拟合已有的理论，处理数据时有强烈的人为取向。

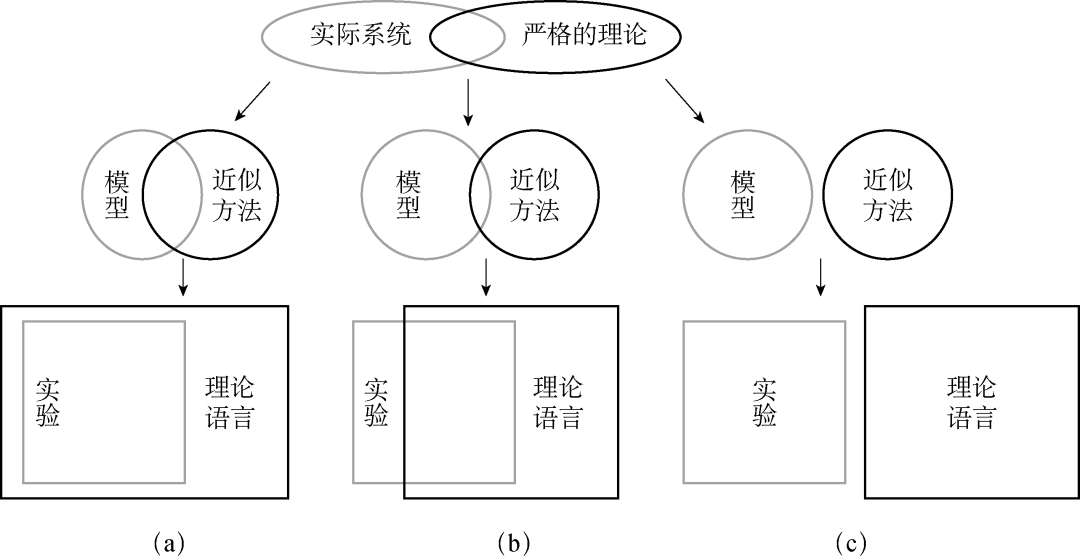
图 3. 实验证实“理论”：实际物理−模型−实验的“距离”决定了“实验证实”工作的好坏。（a）通过好的近似和合适的模型，理论预言涵盖了实际系统的主要物理，实验正好“证实”了它；（b）模型和近似不够理想，理论预言只是反映了实际系统的部分物理，实验证实了其中一部分预言；（c）模型和近似方法偏差较大，实验只是证实了“模型”的预言，并非真实的物理系统。

基于以上考量，我认为，谈及理论预言的实验验证，必须追问到底实验验证了什么。实际物理系统与理想模型是有差距的，基于模型的近似预言与其精确理论结果也存在距离，关于实际物理系统的实验结果和来自模型的近似结果会偏差更远（图 3）！而且其中每一步近似和建模都有不确定的要素，这些不确定性融合在一起，很容易得出“实验验证理论”这一平庸且不严格的结论。在这种情况下，如何避免此类问题的发生，得到可靠的结论，这要基于科学良心对严谨性的执着，科学精神对取得可靠的科学结论是不可或缺的。为了避免“实验验证理论”中人为因素的影响，一个好的理论与实验相结合的工作，必须是双盲的、背靠背的，否则，就会出现理论与实验互相人为迎合的科学诚信问题。

著名化学家朗缪尔（Irving Langmuir）曾经指出[18]，“可能科学家完全是诚实的，十分热衷于自己的研究……但完全自己欺骗了自己”，甚至“这些事件中没有任何弄虚作假，但由于作者不了解作为一个人完全可以被主观的因素、一厢情愿的想象引入歧途，以致完全陷入错误的泥塘之中”。这些主观的因素，完全有可能驱使科学家依据个人偏好，选择性地使用“实验证据”做出“重大科学结论”。一方面，一个好的理论物理成果，要独立放在那里，实验物理学家背靠背独立地验证它的预言；另一方面，一个好的实验，要开放所有认真测量得到的数据，最好让不同理论组背靠背地来解释，给出新发现。需要指出的是，当代物理学的重大发现几乎没有几个是理论和实验直接合作完成，并在一起发表的。这个事实从一个侧面宣示了实验−理论的“背靠背”在科学研究中的不可或缺性。

以上讨论表明理论与实验的关系非言可尽，说一个理论被实验证实了，或者说实验上有一个重要的发现，其内涵并不是显而易见的。从使用数据的可靠程度到理论预言的严谨性，都会影响“证实”之“真”的程度。最近有人发现了室温下的“高压”超导体， 就是同一个人两场闹剧之后的又一场闹剧。

04理论物理研究如何追求可证伪之“真”？

可证伪性（falsifiability）是科学思想家卡尔·波普尔（Karl R. Popper）提出的一种判定理论是否科学的思想原则。他认为，如同“天鹅都是白的”结论一样，一个理论通常是一个全称判断，不可能穷举所有经验来判定它是否正确。因此，越普适的理论越不易证实，但很易证其伪——发现一只黑天鹅，便可以否定上面“白天鹅”的全称命题，因为只观察一只天鹅黑或白，当下在技术上是允许的。从科学哲学的这个角度讲，物理实验只是用来证伪理论物理的预言，而不能完全证实理论。例如，关于 BCS 理论是否被同位素效应所证实，答案是否定的。因为 BCS 只证实了汞等少数元素的同位素效应，大多数元素并不符合 BCS 的“预言”[19]。因此， 不能说超导材料的同位素效应实验能证实了 BCS 理论。其实，理论可证伪性要求启发了一种“求真”“逼真”的科学研究新模式。如果一个理论或假设可以被现有技术发现逻辑上的谬误，我们就说这个理论可证伪，这是判断一个好的理论的逻辑标准，使理论有预言的可检验性，在科研实践中有效且有用，从而达到了科学逻辑之“真”。

现在我们基于理论可证伪性的要求，考察近年流行的量子模拟研究的科学意义究竟如何。理查德·费曼等最早提出的量子模拟， 是指用简易可测、可控的量子系统（甲）去仿真待研究的复杂量子系统（乙），前提是现有理论无法基于现有的计算手段计算出乙的行为。后来量子模拟的概念有一定的引申：模拟实际实验无法实现的物理系统（乙），寻求其新的物理效应和物性。例如，在固体系统中不存在玻色−哈伯德（Bose-Hubbard）模型，但用光晶格中的冷原子能够实现这个理论模型。显然，用“甲”仿真“乙”的目的是为了预测出“乙”未知的效应和物性。但是，是否能通过量子模拟给出关于“乙”的新结果且可以在实验上“证伪”呢？答案基本是否定的。因为系统“乙”复杂得在实验上难控难测、实验条件不易马上实现（否则，何必模拟），用“甲”模拟出“乙”的新知识自然也不易马上被检验——在“乙”自己的实验上进行证伪活动。从这个意义上讲，量子模拟和通常的理论推导一样，一时无法确定和增加可证伪的新知识。正如大卫·休谟（David Hume）指出，“人们不可能诉诸在过去使用归纳推理的成功经验来证明归纳推理的可靠性”，而量子模拟给出“乙”的新知识本质上只是依据对“甲”的归纳推理。量子模拟可以看成从理论到实验的中间环节。既然量子模拟的科学结果不可即时证伪，其可证伪性只有依赖关于“乙”实验技术的未来进步，在逻辑上即时可证伪的特征就不明显了，其研究方法和科学目标都可以被存疑。

还有一些背离量子模拟初心的“量子模拟”，如用难控难测的光晶格冷原子体系模拟简易的一撕即成的石墨烯。除了这种本末倒置的行为，还出现了更平庸的量子模拟。例如，使用光学（或光子）系统去模拟电子系统行为。其实，由于电子系统存在费米面而光子系统没有，它们的统计行为导致的物性和效应完全不同。用光子模拟费米面决定的物性（例如，电子费米面附近低激发的普适行为可以描述为朗道费米液体或 Tomonaga-Luttinger 液体）一定存在原则上的问题。忽略了大量的物理要素一致性的约束，没有费米面，由光子模拟电子经常只是“运动方程”相似性的演示，这种模拟的科学意义自然是要打折扣的。另一方面，能够基于已经被证明的理论精确计算出来的东西也无需模拟，顾此失彼的模拟实验常常没有判定性的意义。有人希望用半导体系统在狄拉克点附近的低激发来模拟基本粒子（图 4），如 Majorana 费米子和外尔（Weyl）粒子。然而，狄拉克点几乎定域在 K 空间的一点，在空间会弥散为一个几率平面波，如此模拟出来的还是想要的粒子吗？因为粒子在空间上必须是定域的。

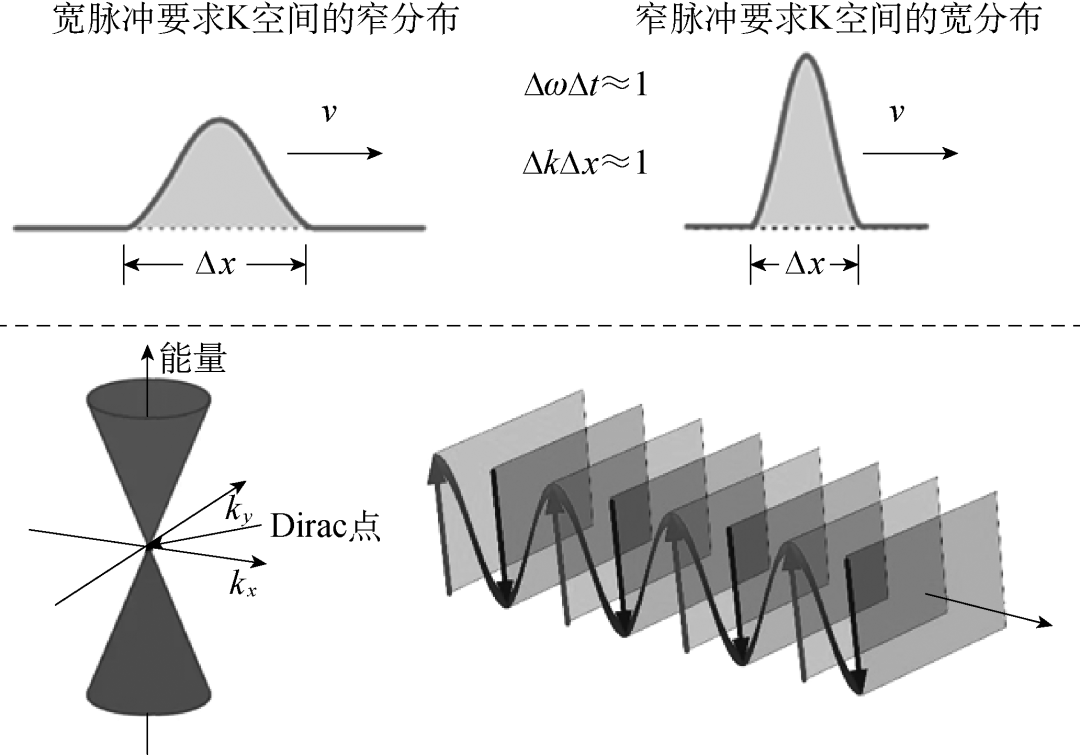
图 4. K 空间几乎局域在一点的“基本粒子”在实空间近乎一个平面波。

我们必须强调，理论一定要联系实际，而实验必须基于理论。然而实验总的目的不只是去证实理论，理论的终极目标也不只是为了去解释实验。实验和理论应该彼此结合起来，去发现新现象、新效应、新物态，找到新规律、建立新方法。这些原则性议论是在讲物理学的发展应当不拘泥一时一事地理论联系实际。爱因斯坦曾经指出，“如果一个理论的基本概念和假设接近于经验，它就具有一种重要的优越性，人们对这样的一种理论自然就有更大的信心…… 然而，随着认识的深入，我们要寻求物理理论基础的逻辑简单性和一致性，因而我们要放弃上述的这种优越性”。在理论物理中，并非每一个理论（推论）都需要直接的实验证实，只有当采用的基本假设无明显理由时才需要实验检验。超导 BCS 理论本质是一种预先假设超导非零序参量的平均场理论，但超导系统粒子数守恒，相应的 U(1)规范对称性通常只能给出序参量为零的结论。因此，我们需要量子隧穿实验（约瑟夫森效应）直接证实非零的序参量的存在从而“证实”BCS 理论。同样，我们也需要昂贵的欧洲大型强子对撞机（LHC）实验，去发现 Higgs 粒子，验证对称自发破缺机制中起关键作用的基本粒子的物理标准模型。另外需要指出，虽然建立在大量实验基础上的量子力学无需进一步检验，但因其预言的非定域效应具有反直观性，也需要验证 Bell 不等式的实验去凸显其量子奇异性[20]。

最后我们指出，“实验验证理论预言”不等于“眼见为实”。其实，虽然夸克是量子色动力学（QCD）建立的基石，但在 QCD 实验中“看”不到自由的夸克，这不等于 QCD 就不对了。QCD 预言的渐近自由效应和夸克禁闭现象，在逻辑上自证自由夸克不存在。这正是杨-Mills 规范理论美妙之处。量子力学的 Everett 多世界诠释在不引入任何额外假设（这隐喻着基于已被实验证实了的假设，等于实验已经检验了）的前提下，从逻辑上能够自证不同分支中无法交换信息——“看不到分裂”，从而给出量子力学的自洽的诠释，展现了量子力学内在的逻辑上的“美”与“真”！其实，QCD 和多世界诠释的某种“真”来自于其“逻辑之美”，它们具有逻辑上的可证伪性。这就是理论物理追求的科学之真和数学逻辑之美！

05理论物理的未来为什么还要面向“有用”？

1961 年，杨振宁先生做过一个题为“物理学的未来”的演讲[[13]， 演讲中对理论物理未来发展的观点看似悲观。虽然当时他在高能物理领域积极推动加速器物理研究，但他那时对理论物理未来发展的“悲观”今天仍然还在：高能物理加速器实验越来越复杂、费用越来越高，理论和实验之间“越来越充满隔膜，而且距离物理的现象越来越远”；虽然“过去的二十年，无论是实验物理或者是理论物理都取得了令人兴奋的进展”，但他“感到今日物理学所遇到的困难有增无减”，他担心“爱因斯坦和我们曾经的大统一的梦想在下一个世纪可能无法实现”。在这种情况下，他继续追问，“21 世纪理论物理学的主旋律是什么呢”？“在充分明白其中可能涉及的风险后”，他做了更大胆的“猜测”：“由于人类面临大量的问题，21 世纪物理学很可能被各种应用问题主导”。

基于这些看法，我在不同场合具象化地阐述过理论物理未来的发展趋势是“应用理论物理”（applied theoretical physics）：基于理论物理的思想、模型和数学工具，以应用为目的，研究主要包括人工复杂系统在内的客观系统，探索其物质−能量、时间−空间和信息− 结构及其相互作用和运动演化规律，从中概括和归纳出具有普遍意义的基本理论，拓展理论物理过去只是关于自然物质系统探究的传统疆域。

从学科属性角度看，应用理论物理学属于“应用基础研究”，是跨系统综合交叉的学科领域。其实，与自由探索的科学研究一样，面向需求的基础研究不仅会导致技术革命，也会引发科学理论原始创新[21]。巴斯德研究酿酒技术相关的酒石酸的偏光行为，导致了生物学的重要分支微生物学的诞生。二战前后关于改进雷达性能的研究，导致了从微波激射器到激光的重要发现[22]。而激光理论后来催生了量子光学、量子通信研究，也推动了今天的精密测量的理论与技术。当然，面向应用领域，理论物理学是否还能演绎出 20 世纪关于对称性、量子化和规范场那样的英雄主题，今天并无确定的答案，但广阔的应用领域至少提供了产生这个旋律的舞台。

我认为，面向应用领域，理论物理未来的研究视野会更趋纵深和广阔。理论物理要立足于全部实验和现象的总和之上，而不是只追逐个别实验和偶然现象。具体的研究工作却要大处着眼，细小处着手。面对当代实验科学日趋复杂和巨大经费需求的形势，理论物理对物理学发展必须发挥更大的引领作用，为高新技术的发展方向提供判定性的科学基础；由于物质世界极为纷繁复杂，理论物理问题的解析求解不足以涵盖复杂系统的全部特征，如非微扰和高度非线性等。因此，理论物理另一个重要发展趋势是将基础理论与强大的现代计算手段相结合，使得理论物理预言更加定量化和精密化。计算物理从而应运而生，成为连接物理实验和理论模型必不可少的纽带。这些计算技术相关的发展，也是应用理论物理应着力倚重的。

理论物理学面对非自然的人工系统，适应物质科学从观测解释阶段进入自主调控的新时代，变自在之物为为我之物。近二十年来，在材料、能源乃至生命方面的实验发现（如生物磁导航、光合作用的量子效应等），在传统的理论物理框架下难以得到解释，新的理论物理创新也迫在眉睫。这些实验发现让理论物理相关应用研究跨上一个新的历史台阶，提供了更多理论物理的引领作用发挥到极致的场所。2021 年的诺贝尔物理学奖颁发给作为复杂物理系统的地球物理和气候的研究工作，或多或少代表了理论物理发展的这样一种趋势。

应用理论物理学在国防安全等国家重大需求上会有更大的用武之地，也会发挥出更大的作用。理论物理学在提升国家战略地位方面已经发挥了不可替代的作用，理论物理学家爱因斯坦、奥本海默、费米、彭桓武、于敏、周光召等人也在这个维度上彪炳史册。例如，周光召利用理论物理的最大功原理，断定了此前我国不同于苏联的“九次计算”结果的正确性，确定了我国当时原子弹研究的正确方向。二战后，美欧开启了物理学大科学工程发展的新时代，基于大型加速器的重大科学发现也反过来为理论物理学提供广阔的用武之地，如标准模型的建立和加速器理论的发展。国防安全方面等国家重大需求往往与大科学工程密切联系，由此会提出自由探索中不易产生的重要基础科学问题，如由雷达发展催生的激光理论与对称性自发破缺机制相关、统计力学的最大熵原理可能会在奠定可靠性分析的理论基础方面发挥重要作用。国防和国家安全方面的重大需求对理论物理不断提出新挑战，同时也为理论物理研究提供了持续源头创新的平台。凝练和发掘应用领域相关的理论物理的科学问题，会在理论原始创新方面孕育重大的科学突破。这方面的研究将是理论物理发展的一个新趋势。

总之，理论物理学在不断“求美”“求真”的同时还要面向“有用”，这是当前社会和科学技术发展的需求，也是理论物理学自身发展的必然趋势。通过将理论成果与实际应用相结合，不仅可以积极推动各个学科之间的交叉融合，促进理论创新、技术革命和跨学科合作，还可以带来更多的经济和社会效益，提升国家的战略地位和竞争力，并为人类文明的进步和发展作出更大的贡献。当然，这里必须注意，在安全保密的屏障下也容易出现“伪需求”和学术造假问题，历史上发生的“汉芯”事件值得引以为戒。

06如何发展基本或（且）有用的理论物理？

以下，我以我们近二十年开展的介观统计热力学（mesoscopic statistical thermodynamics ）研究为例，回顾一下在“专款”支持下，我们的研究工作如何把基础性和应用性结合起来以唯美求真。

介观统计热力学的提法，是用来综合小系统热力学和非平衡统计物理近几十年重要进展，包括量子热力学、非正则统计和热化、有限时间热力学和随机热力学等。这里“介观”的内涵是指系统的空间尺度偏离热力学极限，或者其物理过程的时间尺度可以和“寿命”相比（图 5）。例如，一个有限系统空间尺度可以和单粒子物质波相干长度相比拟，量子效应就起作用了；一个系统的粒子数有限，偏离热力学极限、热力学量的涨落就会明显地起作用。在这种情况下就必须发展量子热力学和小系统的统计热力学，或随机热力学。
 

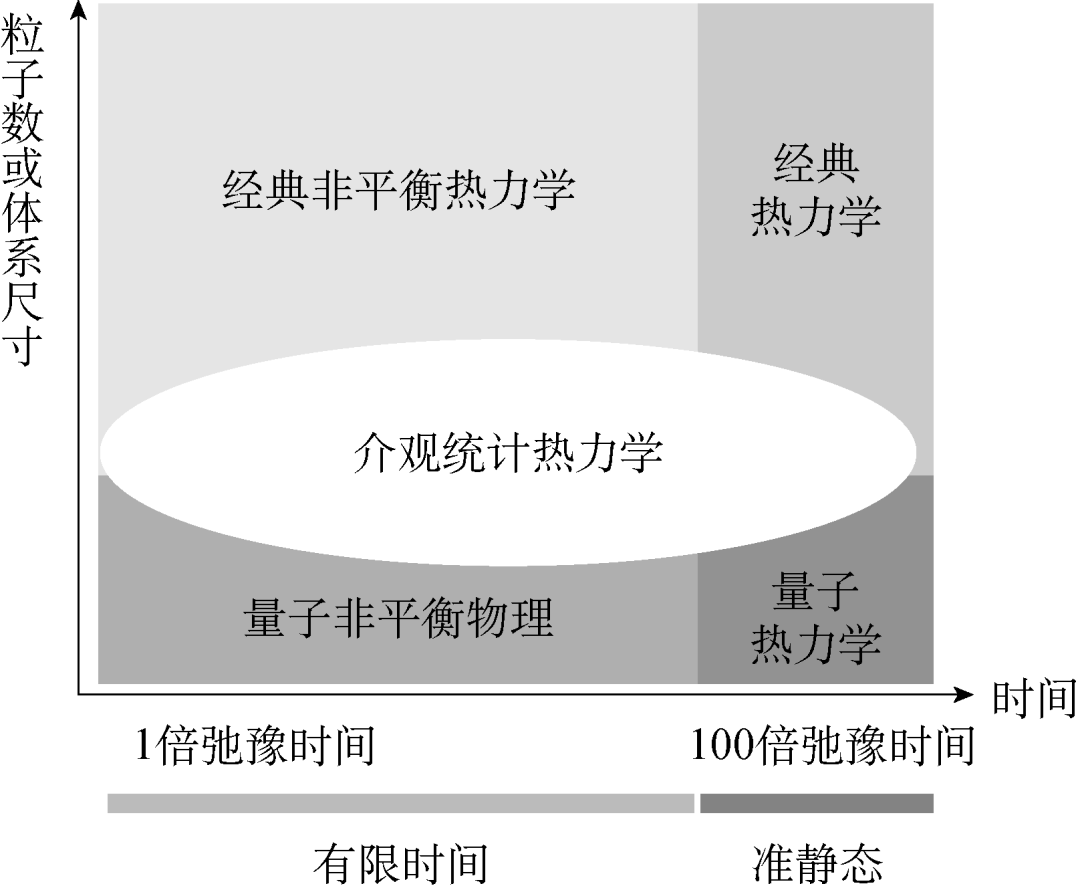
图 5 介观统计热力学的“相图”。

有限时间热力学通常以宏观系统为工作物质，并且用来处理时间有限的准平衡过程。大家知道，一个理想的热机的最高效率是卡诺效率。而其中涉及的热力学准平衡过程需要时间无穷长，因而功率为零。有限时间热力学旨在探索保证功率（效率）最大时的效率（功率）的优化问题，这方面研究与核反应堆的实际应用及内燃机气缸的活塞循环优化控制联系密切。当然，由于时间有限，时间维度上涨落和熵产生变成了这个领域的一个基本问题。最近针对这个问题，我们不仅从理论上完整地确立了一个简洁而优美的功率−效率约束关系[23]，而且自主地设计热力学实验装置，从实验上首次验证了决定功率−效率关系的 1/τ 假设[24]（图 6）。
 

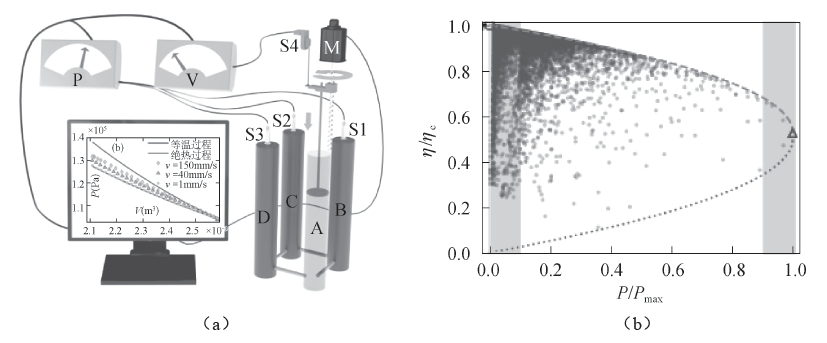
图 6 实验装置图（a）和效率功率关系（b）。

小系统的统计热力学，或随机热力学是过去 30 年左右发展起来的非平衡统计物理的一个分支[25]。它通常以单个或少数几个做布朗运动的介观粒子为研究对象。通过引入运动方程（通常是朗之万方程或福克-普朗克方程）和定义在单条轨道上的功泛函和热泛函，来研究任意远离平衡过程的热力学性质。在经典热力学中，粒子数趋于无穷大（热力学极限），涨落效应不明显，热力学量的平均值就足以描述这个过程。但是在随机热力学中，由于粒子数远小于热力学极限，热力学量的涨落就至关重要。这时，仅使用热力学量的平均值不足以描述这个过程。我们通常需要知道热力学量的所有阶矩的信息，也就是它们的分布函数，比如功分布函数、热分布函数、熵产生的分布函数等。由于有了运动方程，原则上我们可以计算任意远离平衡过程的热力学量的分布函数。在过去 30 年，物理学家还进一步发现，这些热力学量的分布函数满足一些非常普适的恒等式——Jarzynski 恒等式和其他涨落定理。它们对任意远离平衡的过程都成立。这是非平衡统计热力学的重要进展。热力学第二定律以及涨落−耗散定理等在近平衡过程成立的理论则可以被看作是 Jarzynski 恒等式和其他涨落定理的一个推论。因此，这些发现大大加深了我们对热力学第二定律和时间反演对称性破缺的深入认识。随机热力学在过去 30 年与有限时间热力学交织发展，有望为（基于一些唯象假设的）有限时间热力学提供一些微观理论基础。

以下回顾一下我们在“介观统计热力学”领域的研究历程和有关想法。21 世纪初，量子信息和量子计算成为热门的前沿科学领域。此前，我从量子力学测量和退相干问题入手，在 1997 年进入量子计算和量子信息的研究。后来在“专款”支持下，与陶瑞宝先生一道组织了若干次学术讨论会推动国内固态量子计算的研究工作。大家知道，量子纠缠和量子相干可以使量子计算具有经典计算不可比拟的解决特殊问题的能力。虽然直至今天，由于量子退相干的物理约束和技术能力限制，通用量子计算的实用化并没有达到当时预想的目标，但启发了不少新的研究方向，如量子热力学。

在 2002 年的秋天，我产生了一个朴素的意识：既然量子相干性可以本质上突破信息处理的能力瓶颈，那么热机使用量子物质做功是否能突破经典热力学定律对能量传输和转换的限制。当时有人发表文章[26]说，利用相干原子态发光推动微腔活塞，可以实现单一热源做功，从而超越热力学第二定律。我的研究生全海涛、张芃和我从直觉上不相信这个论断。我们从厘清功和热的“量子定义”着手，认真梳理了量子物质做功、放热等基本概念[27]，正确地给出了等温过程、等体过程、绝热过程的描述。我们发现，对于量子做功物质必须正确使用有效温度的观念[28]，从而就不会有破坏热力学定律的反常现象。后来我们进一步尝试了基于“麦克斯韦妖”的信息辅助的量子热机，发现只要把信息擦除的过程包括到热力学循环， 热力学定律就不会被违反。此后，董辉等研究生也陆续加入量子热力学研究，我们进一步从非正则统计物理学、量子相变物质做功和麦克斯韦妖的角度研究相关的问题。这些年量子热力学在世界上成为研究热点，我们早年的几篇文章成为了这个“新兴领域”的代表性工作，至今长引不衰（图 7）。
 

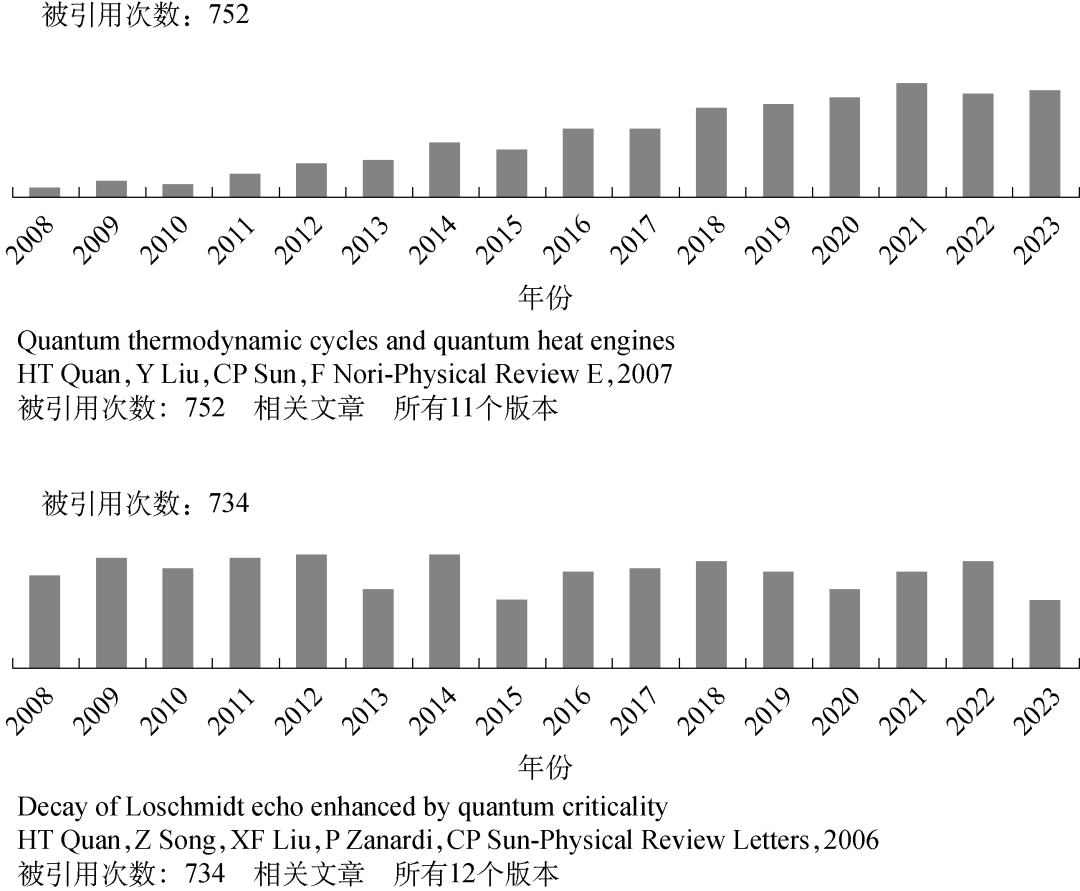
图 7 我们关于量子热力学和量子相变的文章被持续引用或每年引用数不断增长[29]，意味着“介观统计热力学”领域从“基础边缘”已经走到“前沿主流”。

然而，虽然这些工作及时地推动了领域变热，但我们仍然没有初心如愿，对于“可否以量子方式突破热力学定律”的提问，答案仍然不能肯定。于是，我们只能把量子热力学研究暂时放手一下，2012 年起主要精力转到了与之相关的光合作用能量转换的研究。全海涛出国后转入随机热力学研究并有所成就，而董辉在加州大学伯克利分校博士后工作期间转向能量转换的二维光谱理论。此后，我们关于量子热力学的研究沉寂了一段时间。2017 年董辉回国，马宇翰等新同学陆续加入我们组，我们又重新考虑相关问题。不久，我们就意识到有限系统、有限时间情况下有功率−效率优化是个基础且有用的重要科学问题，并且有很强的国家需求背景。我们随后重新启动有限系统、有限时间热力学的理论和实验研究，并完成了一些有意义的工作，如利用参数空间测地线方程、从微分几何的角度讨论做功优化问题等，由此开拓了新的研究方向。

有限系统和有限时间热力学的基础研究与能源物理中的应用需求紧密联系在一起。大量的核电站数据表明，现存核电站的效率基本落在有限时间热力学预测的最大功率效率的约束之下[30, 31]。在保持功率的前提下，提高核电能源转化效率是核电设计中的一个重要问题。第四代核电循环设计在能源效率的提高方面主要依靠内部高温热源温度的提升，把循环物质从传统的水蒸气（320°C）转成氦气（750°C）或者二氧化碳（640°C）[30]。超出上述温度调节的手段之外，是否存在其他方法？这是有限时间热力学在应用中要回答的关键科学问题。近些年有限时间热力学中关于循环控制方式对热力学过程效率影响的研究可能提供超越传统的方法[31, 32]。此外，有限系统和有限时间热力学也会对电路中信息擦除方案的优化和一些关系长时服役的国家重大装备的能源设计提供重要的理论支撑。

从以上研究历程的介绍可以看出，我们从最基本的科学问题和观念出发，逐步走向实验和实际应用，这是一个理论物理“唯美求真”的历程。我们始终坚定初心，让好的科学问题始终牵引我们的研究工作，逐渐逼近有实际意义的应用目标。当然，我们关于介观热力学的研究并没有仅为应用停留在唯象的层面上，我们无时不在探索它们的统计物理的起源。我们发现，有限系统的统计分布是非正则的，它描述了涨落自动内置的非热平衡态。我们还与蔡庆宇等合作，基于更一般的非正则热态[33, 34]，深入探讨了为什么黑洞信息丢失是因为辐射的非正则热态粒子有信息关联。我们进一步把非正则态应用到有寿命涨落的装备可靠性分析中，在一定程度上打通了可靠性工程从技术探索到科学研究的可能途径[35]，希望能对未来长贮装备可靠性和安全性的研究有所实际贡献。

笔者感谢与董辉研究员和全海涛教授关于本文的多次讨论，也感谢所有合作者在介观统计热力学等领域的多年协同探索。还感谢王川西博士在文字方面的协助。

参考文献

[1] 国家自然科学基金委员会, 中国科学院. 未来 10 年中国学科发展战略: 物理学. 北京: 科学出版社, 2012: 1, 2.[2] 理论物理专款学术领导小组. 发展理论物理促进学科交叉——国家自然科学基金理论物理专款 20 周年纪念文集.  北京:  科学出版社, 2013: 18-54.[3] 孙昌璞. 当代理论物理发展趋势之我见——杨振宁学术思想启发的若干思考. 物理学报, 2022, 71(1): 010101.[4] 斯蒂芬·温伯格. 终极理论之梦.  李泳, 译. 长沙: 湖南科学技术出版社, 2018.[5] 斯蒂芬·温伯格. 仰望苍穹: 科学反击文化敌手. 黄艳华,  江向东,  译.  上海:  上海科技教育出版社, 2004.[6] Weisskopf V F. Nuclear structure and modern research. Physics Today, 1967, 20(5): 23- 26.[7] Anderson P W. More is different: Broken symmetry and the nature of the hierarchical structure of science. Science, 1972, 177(4047): 393-396.[8] 张广铭,  于渌, 物理学中的演生现象.  物理, 2010, 39(08): 543-549.[9] 郝柏林.  负戟吟啸录.  新加坡:  八方文化创作室, 2009: 98.[10] 杨振宁.  美与物理学.  二十一世纪, 1997, 40: 71-79.[11] 杨振宁. 美在科学与艺术中的异同.  中国美术馆, 2015, 3: 34.[12] 宋春丹. 王元: 纯粹数学的美丽与哀愁. http://www.inewsweek.cn/people/2021-05- 31/12699.shtml [2021-10-26].[13] 杨振宁. 曙光集.  北京:  生活·读书·新知三联书店, 2018: 1-7.[14] 杨振宁, 翁帆.  晨曦集.  北京:  商务印书馆, 2018: 3-19.[15] 孙昌璞. 量子力学诠释与波普尔哲学的“三个世界”. 中国科学院院刊, 2021, 36(3): 296-307.[16] 庆承瑞, 何祚庥. 科学实验中的“双盲”准则. 现代物理知识, 1996, 8(01): 27-29.[17] Yue X, Qiao G J, Sun C P. Refined Majorana phase diagram in topological insulator- superconductor hybrid system. arXiv preprint arXiv, 2023, 14659.[18] Langmuir I, Hall R N. Pathological science. Physics Today, 1989, 42(10), 36-48.[19] Hirsch J E. Superconductivity Begins with H: Both Properly Understood, and Misunderstood: Superconductivity Basics Rethought. Singapore: World Scientific, 2020.[20] 崔廉相, 许康, 张芃, 孙昌璞. 贝尔不等式的量子违背及其实验检验——兼议2022 年诺贝尔物理学奖.  物理, 2023, 52(1): 1-17.[21] 张慧琴, 王鑫, 王旭, 孙昌璞.  超越巴斯德象限的基础研究动态演化模型及其实践内涵.中国工程科学, 2021, 23(4): 145-152.[22] 王旭, 孙昌璞. 雷达启发的强激光啁啾脉冲技术——军事需求催生基础研究的一个典型案例. 物理, 2019, 48: 1-8.[23] Ma Y H, Xu D, Dong H, Sun C P. Universal constraint for efficiency and power of a low-dissipation heat engine. Phys. Rev. E, 2018, 98: 042112.[24] Ma Y H, Zhai R X, Chen J F, Sun C P, Dong H. Experimental test of the 1/τ-scaling entropy generation in finite-time thermodynamics. Phys. Rev. Lett., 2020, 125(21): 210601.[25] Klages R, Just W, Jarzynski C. Nonequilibrium Statistical Physics of Small Systems: Fluctuation Relations and Beyond. New York: John Wiley & Sons, 2013.[26] Scully M O, Zubairy M S, Agarwal G S, Walther H. Extracting work from a single heat bath via vanishing quantum coherence. Science, 2003, 299(5608): 862-864.[27] Quan H T, Zhang P, Sun C P. Quantum heat engine with multilevel quantum systems. Phys. Rev. E, 2005, 72(5): 056110.[28] Quan H T, Zhang P, Sun C P. Quantum-classical transition of photon-Carnot engine induced by quantum decoherence. Phys. Rev. E, 2006, 73(3): 036122.[29] https://scholar.google.com/citations?user=FkPp4D4AAAAJ&hl=zh-CN)[2023.9.1].[30] International Atomic Energy Agency. Directory of Nuclear Reactors, Ⅸ, Technical Directories. IAEA, Vienna, 1971.[31] Kugeler K, Zhang Z Y. Power Plants with Modular High-temperature Reactor. Berlin: Springer, 2018.[32] Mozurkewich M, Berry R S. Finite-time thermodynamics: Engine performance improved by optimized piston motion. Proc. Nat. Acad. Sci. USA, 1981, 78(4): 1986- 1988.[33] Dong H, Cai Q Y, Liu X F, Sun C P. One hair postulate for Hawking radiation as tunneling process. Commun. Theor. Phys., 2014, 61(3): 289.[34] Ma Y H, Cai Q Y, Dong H, Sun C P. Non-thermal radiation of black holes off canonical typicality. EPL, 2018, 122(3): 30001.[35] Du Y M, Ma Y H, Wei F Y, Guan X F, Sun C P. Maximum entropy approach to reliability. Phys. Rev. E, 2020, 101(1): 012106.

作者简介

孙昌璞，理论物理学家，主要从事量子物理、数学物理和量子信息理论研究。1962年生于辽宁，1984年毕业于东北师范大学物理系，1992年于南开大学获博士学位。2009年11月当选为中国科学院院士，2011年11月当选为发展中国家科学院（原第三世界科学院，TWAS）院士。曾获国家自然科学二等奖、中国科学院青年科学家一等奖、国家教委科技进步一等奖和中国青年科技奖等奖项，以及全国先进工作者和吉林省特等劳动模范等荣誉称号，10次被评为中国科学院“优秀研究生指导教师”和“优秀导师”。曾担任第七届理论物理专款学术领导小组组长。

本文经授权转载自微信公众号“理论物理专款”，原标题为《【专款30周年文集】04. 理论物理的“唯美”与“求真”》。