复杂系统是高维非线性的动力系统，其组成成分之间存在异质相互作用。为了对复杂系统的大规模行为作出可解释的预测，通常假定这些动力学可以简化为几个方程，其涉及描述相互作用网络的低秩矩阵。近日发表于 Nature Physics 的一项新研究关注并探讨这种低秩假设（low-rank hypothesis）的有效性，证实许多复杂系统可以被简化，并且仍然保留初始高维网络的基本特征。研究还表明，高阶相互作用从降维中自然涌现，从而为复杂系统中高阶相互作用的起源提供了启示。本文翻译自伦斯勒理工学院计算机科学系副教授高建喜发表于Nature Physics的评论文章。

评论作者 | 高建喜

译者 | 郭瑞东

审校 | 梁金

我们的世界被极其复杂的系统所包围，从社会结构到大脑中的神经网络[1]。降低这种复杂性的一种典型策略是使用降维技术，从而构建简化模型以探究其复杂对应物的行为。然而，找到这种最佳的维度仍然是一个挑战。近日发表于 Nature Physics 的最新研究[2]，利用“低秩假设”（low-rank hypothesis）为简化模型找到一个合适的维度，确保它能保留初始高维网络的基本特征。

论文题目：The low-rank hypothesis of complex systems论文链接：https://www.nature.com/articles/s41567-023-02303-0

 对复杂网络进行降维的首批方法之一是将系统映射到有效的一维动力学，从而准确预测初始宏观行为[3]。通过对从生态学到生物学再到电网等一系列不同领域的分析进行验证，研究人员发现这种方法能够识别出对确定系统的宏观动力学行为至关重要的三个结构属性：密度、异质性和对称性。 后来的研究通过频谱分析（spectral analysis）的视角提出了各种降维方法[4, 5]。例如，为特定于节点动力学开发的分析框架，允许将复杂的高维网络折叠成由几个控制参数决定的低维流形[6]。这种方法证明了将复杂的动力学浓缩成有效的二维或四维模型的能力[7, 8]，在互惠网络（mutualistic network）的情况下特别成功。另一项值得注意的研究表明，网络系统的动力学可以在不完全了解底层拓扑的情况下进行预测[9]。

这表明，与整个网络的规模和异质性相比，动力学在低维的子空间中运行。尽管这些先前的研究强调了降维技术在网络中的潜力，但设计一种理论来识别最佳维数仍然是一个悬而未决的问题。 由于网络总是可以用矩阵和张量的语言来描述，线性代数为研究网络属性提供了重要的工具。从这个角度来看，降维技术基于一个隐含的假设，即高维复杂系统的动力学取决于低秩矩阵的行为。这项最新研究的目标是探索这个低秩假设的有效性，并描述其对网络上各种动力系统的影响。研究者首先提供了理论证明，在许多广泛使用的随机网络中，假设得到满足，发现这些网络权重矩阵的奇异值迅速下降，这意味着有效秩较低。然后，该团队对许多真实网络进行了广泛的数值模拟，发现这些网络表现出快速下降的奇异值，导致有效秩较低。 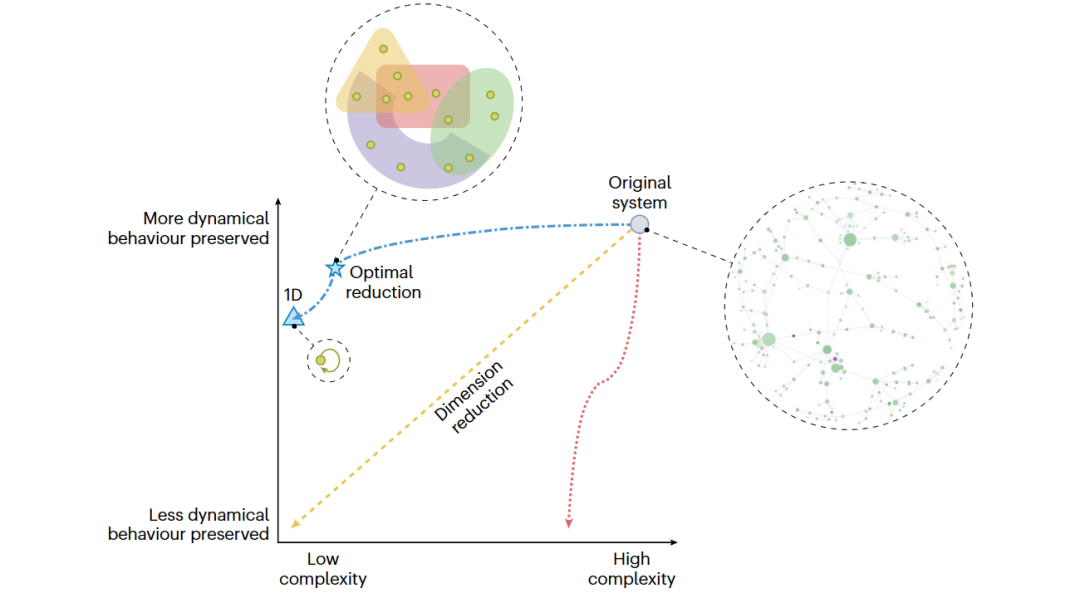图1：高维系统的降维。初始动力系统很复杂，具有许多动力分量。低秩假设表明，降维将导致系统遵循蓝色虚线曲线而不是红色虚线，表示最佳降维（星形），产生高阶相互作用。最终的约简是一维的（三角形）[3] 研究者将动力系统的降维建模为将低维向量场与其初始向量场对齐的问题。最小化对齐误差可产生最佳的降维矩阵。最佳维度取决于它是否保留了初始体系的宏观特性，例如相变或临界点的存在（图1）。约简系统类似于较小网络上的低维动力学，其动力学行为仍然是确定的，例如SIS流行病动力学中的二级相变，Wilson-Cowan动力学中的迟滞相变和循环神经网络动力学中的有限循环。

此外，这些结果为高阶交互作用的涌现提供了见解，因为降维后的矩阵部分决定了超图的方向、加权和符号性质。这些研究结果的一个潜在应用是回答大语言模型是否也是低秩的，以及如何通过低秩假设降低其维数。 谱图（spectral graph）理论的主要缺点是，与更广泛的网络科学提供的见解相比，它缺乏直观的解释。相比之下，植根于图论的网络科学是经验性的，专注于数据，提供直观且易于设计的结构属性，例如度数、聚类系数等等。因此，跨学科研究促进了理解、预测和控制复杂系统的动力学和结构。这项工作提供的见解将丰富数学工具箱，促进各种科学和工程问题的进展，在增强和控制复杂网络系统韧性方面发挥核心作用。

参考文献

[1] Barabási, A. L. Network Science (Cambridge Univ. Press, 2016).

[2] Thibeault, V., Allard, A. & Desrosiers, P. Nat. Phys. https://doi.org/10.1038/s41567-023-02303-0 (2024).[3] Gao, J. et al. Nature 530, 307–312 (2016).[4] Laurence, E. et al. Phys. Rev. X 9, 011042 (2019).[5] Vegué, M. et al. PNAS Nexus 2, 150 (2023).[6] Tu, C. et al. iScience 24, 101912 (2021).[7] Jiang, J. et al. Proc. Natl Acad. Sci. USA 115, E639–E647 (2018).[8] Zhang, H. Nat. Ecol. Evol. 6, 1524–1536 (2022).[9] Prasse, B. et al. Proc. Natl Acad. Sci. USA 119, e2205517119 (2022).[10] Sanhedrai, H. et al. Nat. Phys. 18, 338–349 (2022)

本文经授权转载自微信公众号“集智俱乐部”，本文翻译自 Nature Physics 评论，原文题目“Intrinsic simplicity of complex systems“，原文链接：

https://www.nature.com/articles/s41567-023-02268-0。