在理论上原初黑洞的形成不同于恒星死亡的机制，而是来自宇宙早期能量密度的不均匀性。原初黑洞也是重要的暗物质候选者，近期提出的宇宙一阶相变产生的原初黑洞，在特定能标下可以构成全部暗物质。

撰文 | 郝宇诗（中国科学院理论物理研究所博士研究生）

01

早期宇宙演化历史

现代宇宙学认为宇宙在极早期经历过一次短暂而又剧烈的暴胀阶段，暴胀时期宇宙在极短的时间剧烈膨胀将相关联的两点拉伸到视界之外，暴胀时期的量子涨落成为宇宙结构形成的种子，随着宇宙膨胀温度降低，暴胀场的能量转化为物质粒子，宇宙再次被加热，之后宇宙进入热大爆炸模型阶段，在宇宙诞生后3分钟，宇宙的温度降低到了轻元素可以形成的温标，约100kev，质子与中子合成了轻元素氢、氦、锂。此时的宇宙由辐射主导。随着温度进一步下降，辐射能量密度随尺度因子的负四次方下降，很快就被物质能量密度超过，宇宙进入物质主导时期。在宇宙开始后38万年，由于原子核与电子再复合，光子与电子退耦，从此光子可以自由运动，我们看到的第一束光来自此刻，这就是宇宙微波背景辐射。在对于宇宙微波背景辐射的研究中，我们发现了在几乎均匀的早期宇宙中存在着微小的密度涨落，这一不均匀性带给了我们一种新的区别于天体物理过程的机制来产生黑洞——原初黑洞。

02

原初黑洞

广义相对论预言了黑洞的存在，黑洞是一种致密天体，在它的视界内，时空极度的弯曲导致连光也无法逃逸出黑洞。黑洞只有质量、电荷、角动量三个物理参数。在广义相对论提出后一年，施瓦西得到不含电荷和角动量的黑洞解——施瓦西度规。在 20 世纪 60 年代，克尔求得稳态自旋黑洞解——克尔度规。纽曼将其推广到带电荷的情形，得到克尔-纽曼度规[1-4]。在 20 世 纪 70 年代，黑洞热力学建立[5-7]，霍金发现黑洞视界的表面积不会减小，这与热力学中的熵相似，于是定义了黑洞的熵正比于黑洞视界表面积。然而在之后的研究中，霍金发现在考虑量子效应的情况下黑洞可以向外辐射能量[6]，质量越小的黑洞发出的辐射越强，因此黑洞的寿命有限，越小的黑洞寿命越短。

黑洞可以由恒星死亡形成，在恒星生命末期，恒星燃尽了所有能源，无法再通过核聚变对抗自身引力，当恒星质量大于一定阈值时，它将会塌缩为黑洞。这样形成的黑洞具有质量下限，大约为三个太阳质量。还有一种黑洞并不是由恒星塌缩形成，在宇宙早期暴胀和真空相变可以导致宇宙能量密度的非均匀性，当一个哈勃视界内的能量密度大于周围背景一定阈值时，这片区域将会塌缩为原初黑洞。原初黑洞由霍金在上世纪70年代提出[8]。原初黑洞不同于恒星死亡后形成的黑洞，它的质量分布范围更大，微型黑洞和超大质量黑洞不可能由恒星直接引力坍缩形成（由于霍金辐射，微型黑洞若小于1015克则无法存活到今天），它们只可能来自于早期宇宙的不均匀性。例如银河系中心 106 太阳质量的超大质量黑洞可能就是由这种机制产生的（超大质量黑洞也可以由大质量黑洞作为重种子通过不断吸积合并增长而来）。同时原初黑洞是暗物质的重要候选者，现有的天文观测如宇宙微波背景辐射谱畸变，致密暗物质微晕等给出了原初黑洞质量谱与其暗物质占比的关系，原初黑洞可以占暗物质的多大占比是现在宇宙学关心的重要问题。最近，借助宇宙学一阶相变过程形成原初黑洞[9-11]一度成为研究热点。

03

宇宙学一阶相变产生的原初黑洞

随着温度的降低，水会结冰，这一过程被称之为相变。在宇宙膨胀过程中，温度降低，真空也会由高能的假真空态向低能的真真空态相变。物理图像如下：宇宙起始于亚稳定的假真空态，假真空态有一定概率可以通过量子隧穿效应转变为稳定的真真空态，在假真空背景下不断地有真真空泡泡成核，这些真空泡不断膨胀，碰撞，融合，宇宙中假真空占比不断递减，空间逐渐被真真空泡占据。然而由于相变的随机性，不同哈勃区域的相变开始时刻不同，相变进程也会不同，早开始发生相变的区域已经基本进入低能态的真真空相了，而延迟相变的哈勃区域由于其假真空能量密度并不衰减，因此，即使延迟相变的区域还会随后继续产生零星的真真空泡，其平均能量密度仍会高于早开始相变的区域。那么如果有一片哈勃区域它开始发生相变的时刻明显晚于周围背景，那么它的能量密度就会高于背景能量密度。当密度扰动比值δ高于原初黑洞形成阈值 δc 时，这片哈勃区域就会因为引力塌缩形成原初黑洞。延迟相变时间越晚，密度扰动越明显，形成原初黑洞的时间越早，密度扰动达到 δc 时刻进入视界的尺度所拥有的质量与原初黑洞质量成正比，在引力塌缩过程中会有质量损失。原初黑洞的丰度与可以形成原初黑洞的区域占比，即延迟相变时刻大于可以形成原初黑洞的最小延迟相变时刻的概率有关。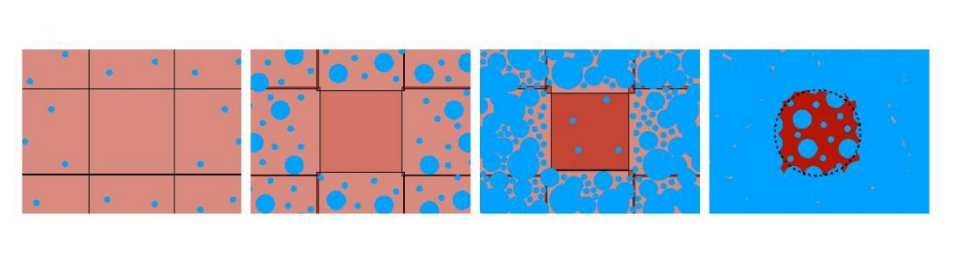

图1：延迟相变机制示意图。红色背景表示高能的假真空态处于辐射主导背景，蓝色泡泡表示隧穿到低能的真真空态区域，从左向后随着时间演进，不断有蓝色真空泡产生，膨胀，逐渐占据整个空间。由于真空泡产生的随机性，示意图仅聚焦于中间某一区域，该区域的相变进程稍微落后于其周围区域，进而从假真空相对真真空的真空能量差中积累了更高的能量密度超出。这部分真空能量密度超出将逐渐主导这块局域延迟相变区域的演化，使其哈勃视界稍稍缩小，等效形成一个局域闭宇宙。当其周围区域几乎已经被蓝色泡泡占据时，这一延迟相变区域才开始有零星的真空泡产生，从而避免该局域真空能量密度主导区域进入永恒暴胀阶段，也就避免了形成婴儿宇宙与当前宇宙断连。这些效应保证了形成原初黑洞的前提条件，使得当这一区域的密度扰动进入视界时，如果其密度超出高于一定阈值，就会通过引力塌 缩形成原初黑洞。[11]

相变的随机性导致了宇宙能量密度分布不均匀，在天文观测中，我们通过曲率扰动功率谱来描述非均匀性的大小。已有的宇宙微波背景辐射谱畸变，致密暗物质微晕等天文观测数据表明宇宙其实是很均匀的，如果相变参数给出的曲率扰动功率谱大于天文观测给出的扰动上限，则该参数空间被排除。在计算宇宙平均扰动时，我们需要对没有产生原初黑洞的各个地方的密度扰动进行积分。由于相变的随机性我们无法预言某区域何时开始相变，但是我们可以计算出它在各个时刻开始相变的概率。因此我们考虑某一特定尺度，将宇宙看作足够多个这一尺度的区域拼接而成，每个区域有一个延迟相变时间，延迟相变时刻早的区域扰动小，反之则具有较大扰动，我们按照延迟相变时间将宇宙各个区域分类，然后对延迟相变时间进行积分，进一步计算得到描述相变过程中宇宙不均匀程度的物理量曲率扰动功率谱。

宇宙学一阶相变产生原初黑洞的机制规避了暴胀原初黑洞的微调问题，在指数相变模型下，在特定能标下可以产生足够多的原初黑洞构成全部暗物质。但是相变是否可以结束（即真空泡是否可以占据全部空间）、产生的原初黑洞是否可以携带角动量、宇宙是否会再次发生相变等问题还有待进一步研究。

参考文献

[1] H. Reissner, “Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie,” Annalen Phys., vol. 355, no. 9, pp. 106– 120, 1916.

[2] R. P. Kerr, “Gravitational field of a spinning mass as an example of algebraically special metrics,” Phys. Rev. Lett., vol. 11, pp. 237–238, 1963.

[3] E. T. Newman, R. Couch, K. Chinnapared, A. Exton, A. Prakash, and R. Torrence, “Metric of a Rotating, Charged Mass,” J. Math. Phys., vol. 6, pp. 918–919, 1965.

[4] E. T. Newman and A. I. Janis, “Note on the Kerr spinning particle

metric,” J. Math. Phys., vol. 6, pp. 915–917, 1965.

[5] S. W. Hawking, “Gravitational radiation from colliding black holes,”

Phys. Rev. Lett., vol. 26, pp. 1344–1346, 1971.

[6] S. W. Hawking, “Black hole explosions,” Nature, vol. 248, pp. 30–31, 1974.

[7] J. D. Bekenstein, “Black holes and the second law,” Lett. Nuovo Cim., vol. 4, pp. 737–740, 1972.

[8] S. Hawking, “Gravitationally collapsed objects of very low mass,” Mon. Not. Roy. Astron. Soc., vol. 152, p. 75, 1971.

[9] J. Liu, L. Bian, R.-G. Cai, Z.-K. Guo, and S.-J. Wang, “Primordial black hole production during first-order phase transitions,” Phys. Rev. D, vol. 105, no. 2, p. L021303, 2022.

[10] J. Liu, L. Bian, R.-G. Cai, Z.-K. Guo, and S.-J. Wang, “Constraining First-Order Phase Transitions with Curvature Perturbations,” Phys. Rev. Lett., vol. 130, no. 5, p. 051001, 2023.

[11] R.-G. Cai, Y.-S. Hao, and S.-J. Wang, “Primordial black holes and curvature perturbations from false vacuum islands,” Sci.China Phys.Mech.Astron. accepted 2024

本文经授权转载自微信公众号“中国科学院理论物理研究所”。