物理学家并没有完全排除隐变量的存在,是否有什么内在固有的东西我们还不了解?我们不知道,我们只知道——量子力学真的非常神奇。
撰文 | Ethan Siegel
翻译 | Hardon
除了我们已经了解并知道如何测量的变量之外,可能还有其他变量。但它们仍然无法使我们摆脱量子诡异的困境。
众所周知,光同时具有波动性和粒子性,正如这张2015年的照片所示。人们不太了解的是,物质粒子也会表现出类似的波动性。即使是像人这样巨大的物体也具有波动性,尽管测量它们极其困难。图片来源:Fabrizio Carbone/EPFL
自人们发现量子系统的奇异行为以来,我们一直被迫应付一个看似令人不安的事实。不管出于什么原因,我们所感知的现实,比如物体在哪里、它们拥有什么属性,并不是从根本上决定的。只要你不进行测量或不与其他系统相互作用,它就处于一个不确定的状态,我们只能从统计学和概率的意义上谈论它所拥有的性质和任何潜在测量的结果。
这是由自然的基本限制导致的吗?在测量完成或量子相互作用发生之前,系统是否存在固有的不确定性?或者是否存在一种“隐藏的现实”,它是完全可预测的、可理解的,并在更深层次上决定了我们所看到的?这种可能性令人着迷,它受到了能跟爱因斯坦比肩的科学家的青睐。这也是Patreon(某众筹平台)支持者William Blair的疑问,他说道:
“Simon Kochen和Ernst Specker从纯逻辑推理的方式论证了量子力学中不存在所谓的隐变量。我查了一下资料,但这些文章中的数学和物理超出了我的理解水平。你能启发我们吗?”
实在性是很复杂的,尤其是涉及到量子现象时。让我们从量子不确定性最著名的例子开始,它就是海森堡不确定性原理。
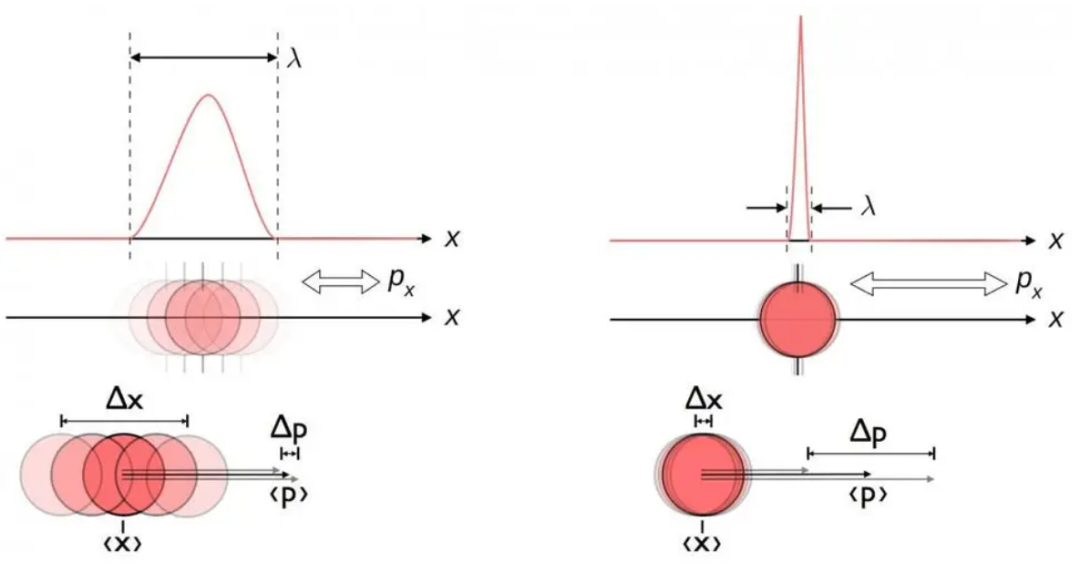
该图说明了位置和动量之间固有的不确定关系。当我们对两者之一了解得越多时,对另一个从根本上就不可能了解得很精确。其他共轭变量对,包括能量和时间、在两个垂直方向上的自旋、角位置和角动量,也表现出相同的不确定性关系。图片来源:Maschen/Wikimedia Commons
在经典的宏观世界里,不存在所谓的测量问题。比如拿任何你喜欢的物体来举例,一架喷气式飞机、一辆汽车、一个网球、一块鹅卵石,甚至是一粒尘埃,你不仅可以测量它任何你想要了解的属性,还可以根据我们已知的物理定律,推断出这些属性在很远的未来将是什么样子。牛顿运动定律、爱因斯坦方程和麦克斯韦方程组都是确定性的,如果你能告诉我你所指定的系统或者说宇宙中每个粒子的位置和运动状态,我就能准确地告诉你在未来的任意时刻,它们将出现在哪里,怎样运动。我们唯一的不确定因素来自于我们用来做测量的设备的限制。
但在量子世界中,情况不再如此。量子世界中存在一种内在的不确定性,你能多大程度地同时了解物体各种各样的性质,是不确定的。例如,如果你试着测量一个粒子的:
位置和动量;
能量和寿命;
在任意两个垂直方向上的自旋;
或者角位置和角动量;
你会发现同时知道这两个量是有限制的,它们不确定性的乘积不能小于某个基本值,并且正比于普朗克常数。
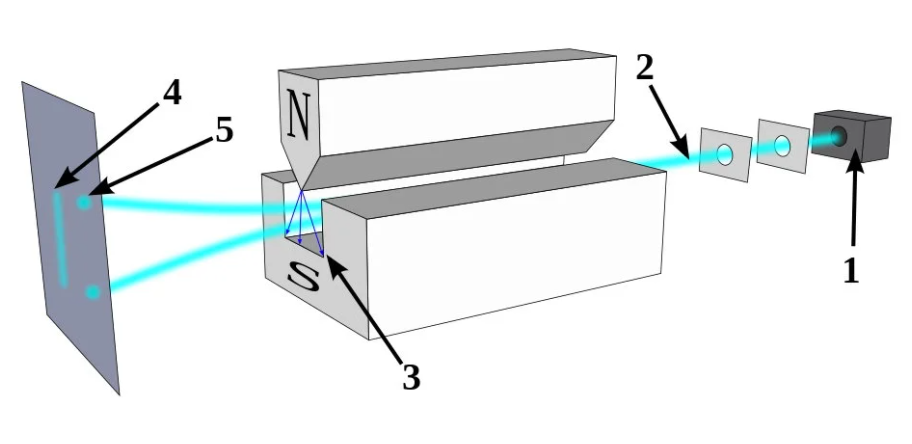
通过磁铁的粒子束可能产生因粒子自旋角动量导致的量子化-离散的结果(5),或者是经典-连续的结果(4)。这个实验被称为斯特恩-格拉赫实验,它展示了一些重要的量子现象。图片来源:Tatoute/Wikimedia Commons
事实上,当你把其中一个量测量得非常精确的时候,另一个互补的量的不确定度就会自动增加,它们的乘积总是大于某个特定的值。如上图所示的斯特恩-格拉赫实验就是一个例子。像电子、质子和原子核这样的量子粒子都有一个内禀的角动量,我们称之为量子“自旋”,尽管这些粒子没有任何实际上的自旋。在最简单的情况下,这些粒子的自旋为1/2,无论你在哪个方向测量它,它都可以是正(+½)或负(-½)。
现在,奇怪的地方来了。假设我们发射这些粒子(在最初的实验中使用的是银原子)通过一个特定方向的磁场。一半的粒子将会向一个方向偏转(对应于自旋= +½的情况),一半的粒子会向另一个方向偏转(对应于自旋= -½的情况)。如果再让这些粒子通过另一个方向相同的斯特恩-格拉赫装置,就不会有进一步的分裂,也就是说+½粒子和-½粒子会“记住”它们分裂的方向。
但是如果你让它们再通过垂直于第一个方向的磁场,它们会再次在正方向和负方向分裂,就好像在这个新的方向上,仍然存在不确定性——哪些是+1/2,哪些是-1/2。现在,如果你回到原来的方向再施加一个磁场,它们会再次在正负方向上分裂。在某种程度上,在垂直方向上测量它们的自旋不仅“确定”了这些自旋,而且在某种程度上破坏了你之前知道的关于初始分裂方向的信息。
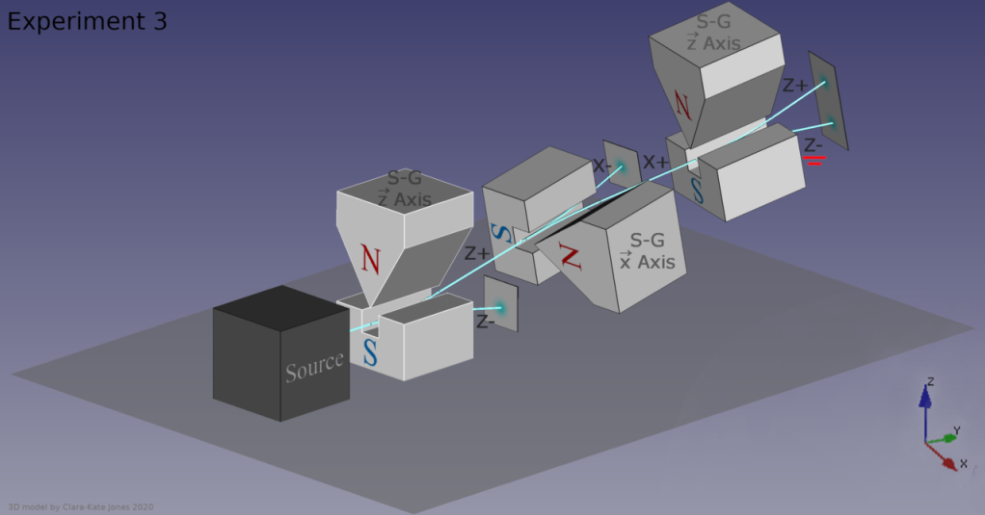
当你让一组粒子通过一个斯特恩-格拉赫磁铁时,它们会根据自旋而偏转。如果你让它们通过第二个垂直的磁铁,它们会在新的方向上再次分裂。如果再加入第三个磁铁,并且和第一个方向相同时,粒子束会再次分裂,证明之前获得的确定的信息将被最近的测量随机化。图片来源:MJasK/Wikimedia Commons
对这个问题的思考让我们意识到量子世界有一种固有的不确定性,这种不确定性永远无法被完全消除。当你在某一个维度中精确地确定粒子的自旋时,在其垂直维度中相应的不确定性必须变得无限大来补偿,否则就会违反海森堡的不等式。我们无法“欺骗”不确定性原理,只能通过测量来获得关于系统实际结果的信息。
但长期以来,人们一直尝试用另一种想法来解释这是怎么回事,那就是隐变量理论。在隐变量理论中,宇宙是决定性的,量子具有内禀的特性,这使我们能够准确地预测它们最终会在出现在哪里,以及任何量子实验的结果会是什么。但是在我们目前现实世界中,一些控制这个系统行为的变量无法被我们测量。如果可以测量,我们就会明白,我们观察到的这种“不确定”行为只是因为我们对真实情况的无知;如果我们能找到、识别和理解这些构成现实基础的变量的行为,量子宇宙就不会显得那么神秘了。

尽管在量子层面上,实在性似乎是变化无常的、不确定的,而且本质上是无法确知的,但许多人坚定地相信,可能存在我们看不见的性质,这些性质决定了独立于观察者的客观现实的真实情况。截至2022年底,我们还没有发现任何此类证据。
我对隐变量的设想是,想象在量子尺度下的宇宙,有一些我们尚未理解但可以观察到其作用的动力学。这就像在我们现实的底部连接着一个振动板,而我们只可以观察到板上的沙粒。
如果你所能看到的只是沙粒,那么在你看来,每一粒沙粒的振动都带有一定的内在随机性,且沙粒之间甚至可能存在大尺度的模式或相关性。然而,因为你不能观察或测量颗粒下面的振动板,你就无法知道控制系统的完整的动力学。你能了解到的信息是不完整的,看似随机的东西实际上有一个根本的解释,尽管我们还没有完全理解。
这是一个值得探索的有趣想法,但就像我们物质宇宙中的所有事物一样,我们必须始终通过对实际物质的测量、实验和观察来证实我们的想法。

“蒙面”双缝实验的结果。注意当第一个狭缝(P1)、第二个狭缝(P2)或两个狭缝(P12)都打开时,看到的图案将非常不同,这主要取决于有一个还是两个狭缝是打开的。图片来源:R. Bach et al., New J. Phys., 2013
在我看来,有一个这样的实验,是所有量子物理学中最重要的实验——那就是双缝干涉实验。当你取一个量子粒子向双缝发射,你可以在背景屏幕上测量粒子落在哪里。如果你这样做了数百次,数千次,甚至数百万次,你最终将能够看到出现的图案是怎样的。
这时最奇怪的地方出现了。
1.如果你不测量粒子通过了两条狭缝中的哪一条,你就会得到干涉图样,粒子倾向于出现在某些地方,而在这些地方之间粒子极不可能出现。即使你让这些粒子一次一个地通过,干涉效应仍然存在,就好像每个粒子都在与自己干涉一样。
2.但是,如果你测量每个粒子具体通过哪一个狭缝,比如用光子计数器、标记或任何其他机制,干涉图案就不会出现。此时你只能看到两个团块,一个对应于穿过第一个狭缝的粒子,另一个对应于穿过第二个狭缝的粒子。
如果我们想进一步确定宇宙中到底发生了什么,我们还可以进行另一种类型的实验——量子延迟选择实验。
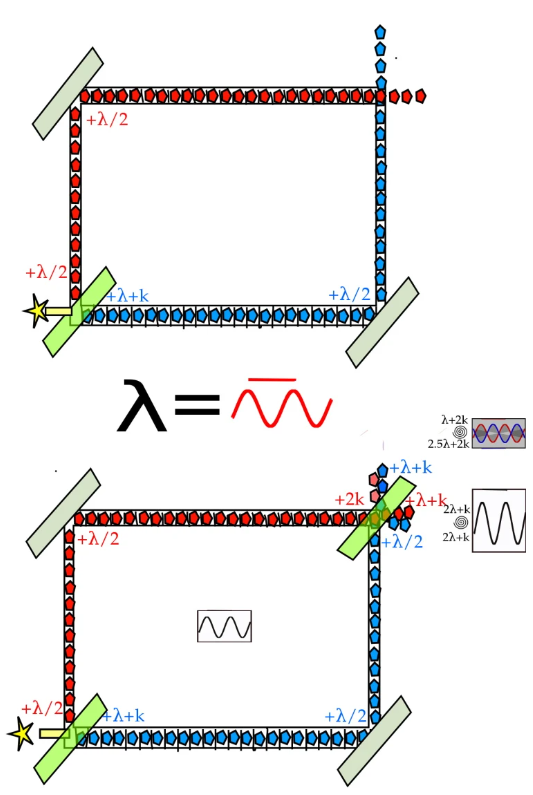
这张图说明了惠勒延迟选择实验。在上图中,光子先通过分束器,在这里它将选择红色或蓝色的路径,并到达两个探测器之一。在下图中,在末端放置了第二个分束器,此时路径将组合产生干涉图案。延迟配置的选择对实验结果没有影响。图片来源:Patrick Edwin Moran/Wikimedia Commons
约翰·惠勒是20世纪最伟大的物理学家之一。(编者注:参见《在与时间的斗争中,他改变了物理学》)惠勒一直在思考量子“怪异”的行为,比如这些量子是如何做到有时表现为粒子,有时表现为波的。当他开始设计实验,试图捕捉期望表现为粒子行为的量子时,它们却表现为波的行为,反之亦然。也许这些实验中最能说明问题的是如上所示的实验,让光子通过分束器进入干涉仪,干涉仪有两种可能的配置,“开”和“闭”。
干涉仪的工作原理是将光分到两个不同的方向,然后在最后将它们重新组合,根据两条路线之间的路径长度(或光传播时间)的差异产生干涉图案。
1. 如果配置为“开放” (上图),你可以简单地区分来自两个路径的光子,而不会得到组合的干涉图案。
2. 如果配置是“关闭” (下图),你会在屏幕上看到类似波的效应。
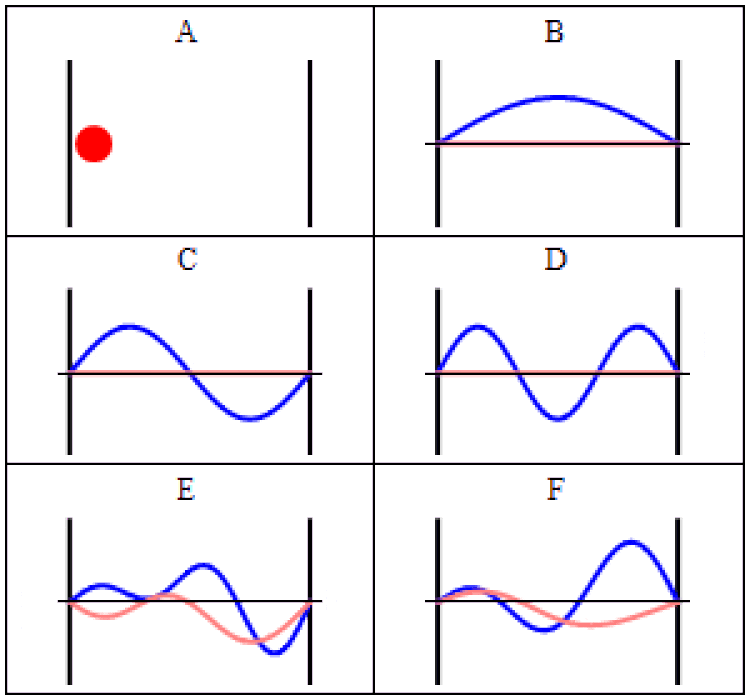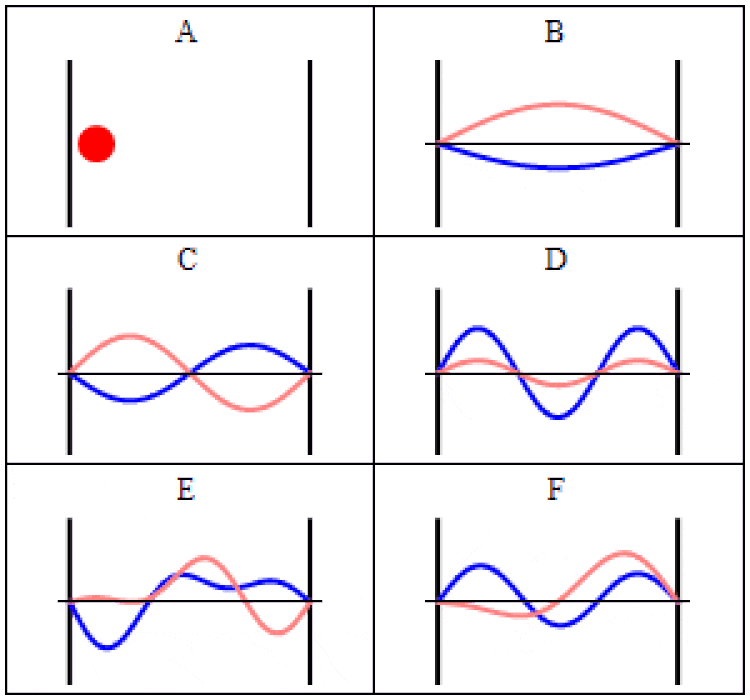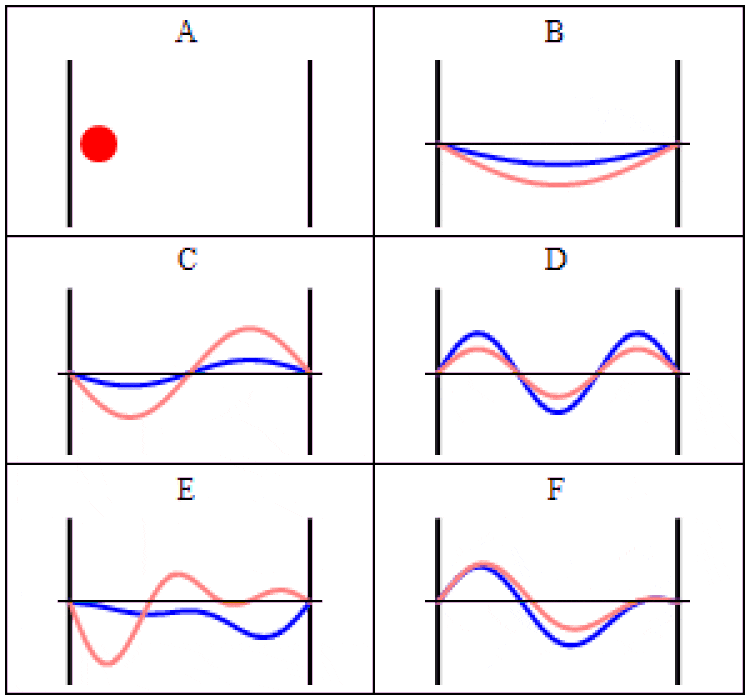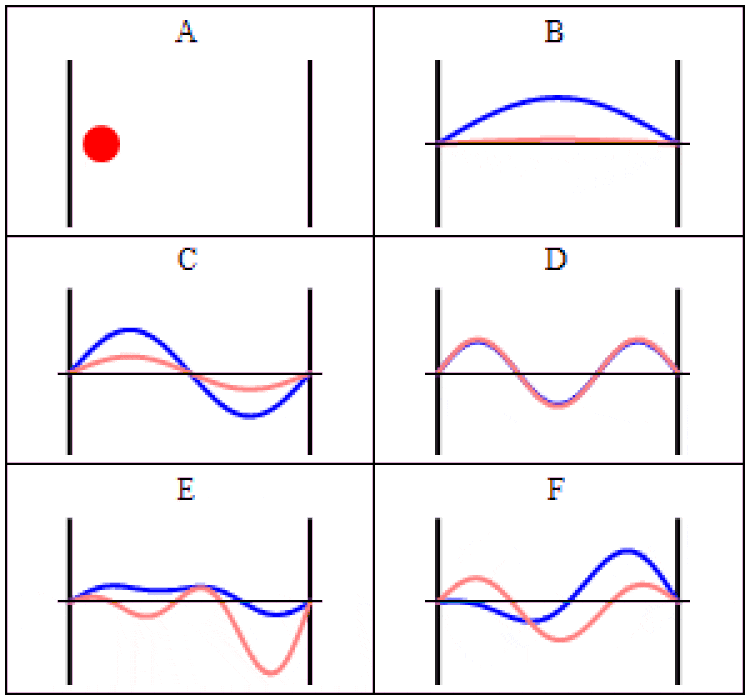
在经典力学(a)和量子力学(B-F)中,粒子在盒子(也称为无限深方势阱)中的轨迹。在(A)中,粒子以匀速运动,来回弹跳。(B-F)为时间依赖的薛定谔方程的波函数解,各图中势场的几何形状和强度都相同。横轴为位置,纵轴为波函数实部(蓝色)或虚部(红色)。这些稳态(B, C, D)和非稳态(E, F)只能表示粒子出现的概率,而非粒子在某个特定时刻出现的具体结果。
惠勒想知道的是,这些光子是否事先“知道”它们必须如何行动。他假想以某一种配置开始实验,然后在光子到达实验终点之前,在最后“打开”或“关闭”仪器。如果光知道它要做什么,你就能在它成为波或粒子的过程中捕捉到它。
然而,在所有情况下,当量子到达时实验终点时,它们的行为与你的预期完全相符。在双缝实验中,当它们通过一个缝时,如果你与它们相互作用,它们就会表现为粒子,而如果你不与它们相互作用,它们就会表现为波。在延迟选择实验中,如果重组光子路径的最终设备在光子到达前出现,你就会得到类似波的干涉图案;如果是另一种情况,你只能得到单个光子而不出现干涉。正如尼尔斯·玻尔(爱因斯坦在量子力学不确定性问题上的最主要的争辩者)所说:
“……就一个明确的实验设置所能获得的可观察效应而言,无论我们构造或操作仪器的计划是事先确定的,还是我们选择推迟计划,这时粒子正在在从一个仪器到另一个仪器的过程中,这两者应该是没有区别的。”
但这是否排除了可能存在隐藏变量支配着量子宇宙的想法呢?不完全是。它所做的是对这些隐藏变量的性质做了重要的约束。自1964年从约翰·斯图尔特·贝尔(John Stewart Bell)开始,多年来许多人已经表明,如果你试图为我们的量子现实保留一个“隐变量”解释,就必须给出其他重要的东西。
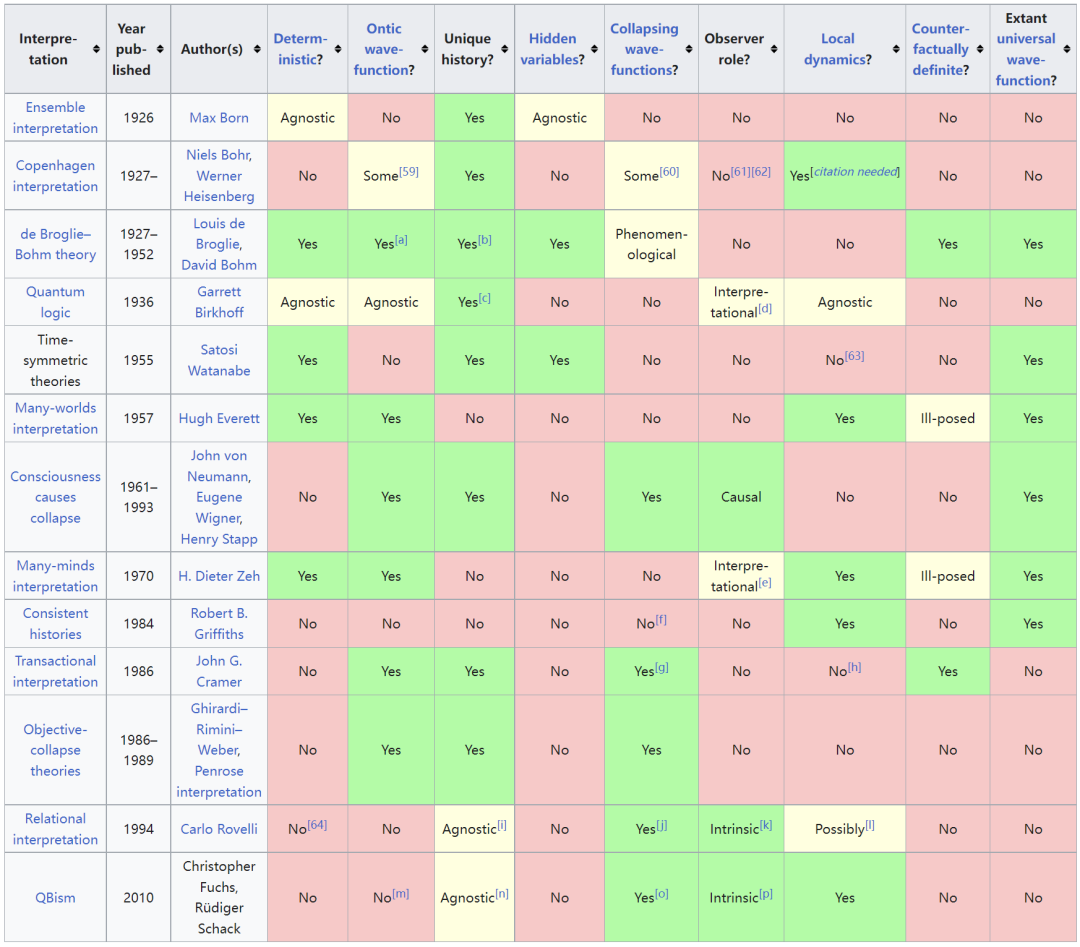
各种量子诠释以及各种性质的匹配。尽管存在差异,但尚无已知实验可以区分这些不同的解释,尽管可以排除某些诠释,例如具有局域性、实在性、确定性隐变量的诠释。图片来源:English Wikipedia page on Interpretations of Quantum Mechanics
在物理学中,我们有局域性(locality)的概念,即任何信号的传播速度都不能超过光速,信息只能在两个量子之间以光速或更低的速度传播。贝尔首先表明的是,如果你想要发展一套量子力学的隐变量理论,并且它与我们所做的所有实验结果相符,那么这个理论必须存在非局域性,一些信息必须以大于光速的速度交换。根据经验,信号只能以有限的速度传输,如果我们要求发展量子力学的“隐变量”理论,局域性是我们不得不放弃的东西。
那么,关于Kochen-Specker定理呢?这个定理是贝尔的理论提出之后几年出现的。它指出,你不仅要放弃局部性,还必须放弃所谓的量子非互文性(quantum noncontextuality)。简单地说,这意味着你所做的任何实验,所给出该系统任意量子性质的测量值,它不仅仅是事先确定的“揭示预先存在的值”。
相反,当你测量一个量子可观测值时,你获得的值取决于我们所说的“测量上下文”,即与你关注的量同时被测量的其他可观测量。Kochen-Specker定理是第一个表明量子互文性(即任何可观测量的测量结果依赖于系统内所有其他可观测量)是量子力学的内禀特性。换句话说,你无法给由量子实验揭示的基本物理量赋值而不破坏它们之间的关系,而这些关系对量子宇宙的运作至关重要。
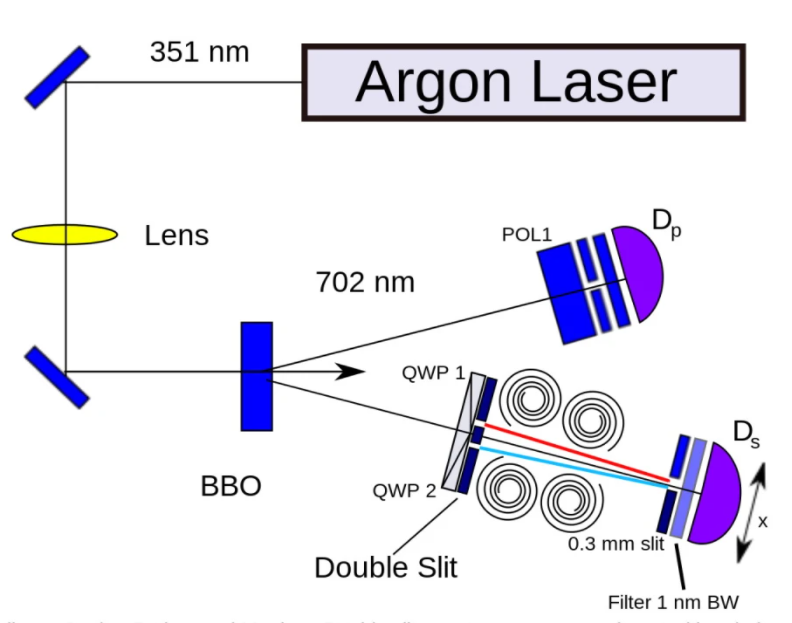
量子擦除实验装置。两个处于纠缠态的粒子分离后分别被测量。一个粒子在终点的改变不会影响另一个粒子的结果。你可以把类似于量子擦除之类的原理和双缝实验结合起来,看看如果你保留或破坏、观察或不观察,那些因通过狭缝被测量而创造的信息本身会发生什么。图片来源:Patrick Edwin Moran/Wikimedia Commons
当谈到物质宇宙时,我们总是要记住的一件事是,无论我们对自己的逻辑推理和数学的合理性有多确定,现实的最终仲裁者还是以实验结果的形式出现的。当你了解我们所做的实验并试图推导出支配它们的规则时,你必须得到一个自洽的框架。尽管量子力学有无数种诠释都能同样成功地描述现实,但从来没有人不同意最原始(哥本哈根)诠释的预测。对某一种诠释的偏好,许多人出于我无法解释的原因而拥有这种偏好,只不过是意识形态的不同。
没有什么能阻止你假设存在一个额外的、潜在的、真正支配现实的隐变量集。然而,Kochen-Specker定理告诉我们的是,如果这些变量确实存在,它们不会预先确定实验结果所揭示的值而独立于我们已知的量子规则。这种被称为量子互文性的实验实现,现在是量子基础领域中的一个广泛的研究领域,对量子计算有影响,特别是在加速计算和追求量子霸权的领域。这并不是说隐变量不存在,而是这个定理告诉我们,如果你想调用它们,你必须耍这样的花招。
不管我们有多不喜欢它,量子力学固有的某种“怪异”是我们无法轻易摆脱的。你可能对一个根本不确定的宇宙的理论感到不舒服,但其他的诠释,包括那些含隐变量的诠释,也同样奇怪。
作者简介

Ethan Siegel,天体物理学家、作家和科学传播者,教授物理学和天文学。自2008年以来,其博客“从大爆炸开始”(Starts With A Bang!)赢得了很多科学写作奖,包括物理研究所颁发的最佳科学博客奖。作者并著有:Treknology:The Science of Star Trek from Tricorders to Warp Drive,以及Beyond the Galaxy等。
本文经作者授权发表于《返朴》,原文发表于
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 