在固体理论研究早期,电子被认为是满足牛顿力学的经典粒子。随着20世纪前半段量子力学的逐步建立,微观粒子的波动性成为精确理解微观世界的关键。这也深刻影响了人们对晶体中电子的认识:电子以布洛赫波的本征形式存在于晶体中,而其粒子性则以波包形式在大于晶格间距的空间尺度上存在。自1980年以来,人们发现布洛赫波的几何相位在固体理论中不可或缺,这进一步完善了晶体中电子的粒子观。文章旨在跟随整个固体物理研究框架的进展勾画出电子粒子观演变的大致轮廓,以一些关键物理问题为例解释电子粒子观的内涵并展示其在固体物理研究中的价值。
撰文 | 牛谦(中国科学技术大学物理学院)、高阳(中国科学技术大学物理学院)
来源 | 选自《物理》2024年第1期
粒子和波动是物质世界为我们所熟知的两种基本形态。二者实为一体之两面,既相互对立又和谐统一。历史上,伴随着电动力学的成熟与量子力学的兴起,我们对光的认识就经历过从粒子到波动再到粒子的演变。对于电子,我们的认识起于阴极射线粒子,但对于原子壳层结构的理解迫使人们接受了它的波动属性,让物理界经历了另一场触及灵魂的量子变革。相较于原子的微小尺寸,电子在固体中的活动空间更为广阔,使它又能以粒子的形态出现,贯穿于我们的思考和话语中。
固体物理的叙述有三大版块[1]:结构、粒子、响应。其中,“结构”包括原子以及某些物理量 (如自旋) 在空间的秩序;“粒子”包括电子和其他元激发 (如声子) ;“响应”则指固体在力、热、声、光、电、磁等方面对外界激励的反应。作为基本粒子,电子通过与原子核以及其他电子之间的量子多体相互作用,不仅撑起了原子的壳层结构,也为固体结构提供了粘合,从而成为联结微观单元与宏观秩序的关键。电子在固体的响应中亦常起着主要作用,而其中反应最积极的部分往往会以某种崭新的粒子形态出现。
经典力学中的粒子概念源于一种对宏观物体的抽象:强调其质心的位置和动量而忽略其内部结构。阴极射线中的电子在电磁场下的行为也确实像一种带电的经典粒子,但原子尺度下的电子状态需要用量子波函数来描述。本文关注具有周期结构的材料中的电子,回顾它如何经历量子力学改造,在大于原子尺度上脱颖而出成为一种新型粒子。新电子遵从一套全新的粒子运动方程,相互独立但满足费米—狄拉克量子统计,简洁有效地为材料的微观结构与宏观性质搭起桥梁。
人们对固体物理中电子的认识已历时百年[2—4]。早期,旧量子论的先驱索末菲 (Arnold Sommerfeld) 把量子统计引入自由电子气理论,解决了电子的比热和热输运问题中的困难。接着,布洛赫 (Felix Bloch) 结合量子波动方程与固体中的周期性势场,提出了布洛赫粒子的概念。基于此,人们初步勾画出了金属、半导体、绝缘体的基本图像。二战后,又经过几十年的努力,人们细致地梳理了电子的多体相互作用,展开了对布洛赫态的第一性原理计算。同时,人们也系统研究了布洛赫能带在外场下的量子响应,并重拾布洛赫粒子的波动诠释。上世纪80年代,索利斯 (David Thouless) 等人对量子霍尔效应的研究开启了对布洛赫电子的拓扑性质的关注。与此紧密相关,贝里相位与贝里曲率对布洛赫电子的影响也逐渐明确,重塑了人们对固体中电子的认识。
01
经典电子图像
1897年,汤姆孙 (Joseph Thomson) 发现从低压气体放电管阴极发出的射线是一种带电粒子,并通过其在电磁场中的加速和偏转,测定出了荷质比[5,6]。人们后来将其称为电子。它的发现揭开了人们从理论层面严谨地研究原子分子和固体物理的篇章。仅仅三年后,德鲁德 (Paul Drude) 建立了金属导电的微观图像[7]:一群自由电子在电磁场作用下加速,而由碰撞散射导致的摩擦力使运动稳定下来形成正比于电场的电流 (参见Box 1)。这个图像把电导率与电荷密度以及碰撞间的距离 (平均自由程) 或时间 (弛豫时间) 唯象地联系了起来。其关于霍尔电阻率的预言很特别:横向电场与电流和磁场的比值只依赖于电荷密度,而与弛豫时间无关。基于此,人们发展出了材料中载流电荷密度的标准测量方法。
BOX 1
德鲁德自由电子模型
在1900年,德鲁德构建了导体导电的理论模型,也即著名的德鲁德自由电子模型。其对电导和热导的解释展示出即使朴素的粒子图像也可成为认识固体宏观性质的拼图。德鲁德认为导体中有等量的正负粒子,故其整体呈电中性。但正负粒子可自由移动,故可产生电流。这里为简化起见,我们只考虑其中的负电粒子,也即电子。其运动规律遵循经典的牛顿力学方程:
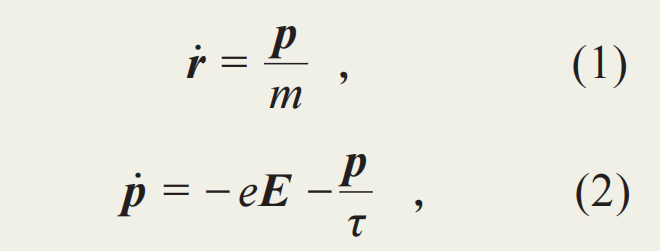
其中,r、p、e、m、τ分别是电子的位置、动量、电荷量、质量和弛豫时间。方程(2)给出粒子的受力:第一项为通常的电场力,它会使动量均匀的变化;第二项为摩擦力,它使得粒子的动量趋于零。二者抗衡的结果使得粒子不能一直被电场加速,而是会达到一个稳定值,即pf=-eτE。根据方程(1),此动量对应一个稳定速度,从而可产生净电流: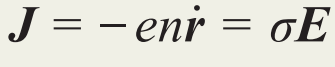 ,其中n为电子密度。对应的电导率σ即为σ=ne2τ/m。电导率的倒数是电阻率,它是我们所熟知的欧姆定律中的电阻与材料尺寸无关的部分。
,其中n为电子密度。对应的电导率σ即为σ=ne2τ/m。电导率的倒数是电阻率,它是我们所熟知的欧姆定律中的电阻与材料尺寸无关的部分。
热导率也可在自由电子模型的框架之下获得,但由于温度梯度是带有统计性质的力,其驱动的热流不能简单地由运动方程给出。我们在这里简单解释下计算热导率的思路,而省去具体过程。根据能量均分定理,粒子的动能的统计平均值正比于其温度,也即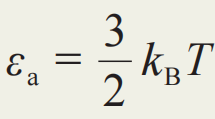 。沿相反方向运动的电子来自于不同的地方,它们的位置差异也带来温度的差异,从而携带方向相反且大小不同的热流。具体计算表明,净热流正比于温度梯度,即Jq=-κ∇T,而热导率由
。沿相反方向运动的电子来自于不同的地方,它们的位置差异也带来温度的差异,从而携带方向相反且大小不同的热流。具体计算表明,净热流正比于温度梯度,即Jq=-κ∇T,而热导率由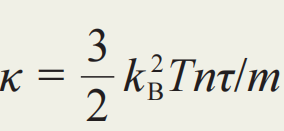 给出。
给出。
当我们用热导率除以电导率,弛豫的信息被精准消除: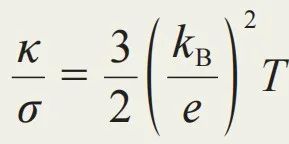 。由德鲁德自由电子模型所给出的热导率和电导率的比值与弛豫过程无关的结论与实验十分相符。而由于当时理论的不严谨性,德鲁德给出的数值系数也与量子理论的预言值(π2/3)非常接近。这曾被认为是自由电子模型非常成功的一个例证。
。由德鲁德自由电子模型所给出的热导率和电导率的比值与弛豫过程无关的结论与实验十分相符。而由于当时理论的不严谨性,德鲁德给出的数值系数也与量子理论的预言值(π2/3)非常接近。这曾被认为是自由电子模型非常成功的一个例证。
德鲁德的微观图像也可以用来讨论热传导问题。一个初级考虑是,自由飞行至某处的电子曾来自于不同的碰撞点,而基于经典统计的能量均分定理,从高温处来的电子速率会相对大些。这意味着电子倾向于离开高温区域而流向低温区域,导致正比于温度梯度的热流 (傅里叶定律) 和电流 (泽贝克定律)。他进一步发现,如果用热导率除以电导率,弛豫时间可以消掉。此结果正比于温度,而比例系数是由电子电荷和玻尔兹曼常数组成的普适常数。他的计算值与当时实验结果 (维德曼—弗兰兹定律) 吻合度很高,曾被归为其理论成功的一面。但若把热电导率 (泽贝克系数) 和电导率相除,虽也可消掉弛豫时间,其结果却比实验值大两个数量级。
当然,电导率等本身还是正比于弛豫时间的。如何解释其量级和温度依赖关系也让人们伤透了脑筋。洛伦兹 (Hendrik Lorentz) 曾在这个问题上花了大力气,用19世纪以来建立的高级输运理论系统地研究了一番[8]。从经典统计分布出发,在弛豫时间近似下,他基本重复了德鲁德的结果。他还设想了微观机制来具体求出弛豫时间,比如电子被周期排布的正离子实散射。但其预言的结果总是与实验大相径庭。
尽管有诸多缺陷,德鲁德的简单直观的输运图像仍流传至今,并被人们用来描述各种实验结果。这是因为在洛伦兹之后,它经受过几次量子力学的重大改造。其中首次改造由泡利 (Wolfgang Pauli) 和索末菲等人完成:他们为自由电子气体加持了量子统计。索末菲曾参与构建原子的玻尔量子模型,并引入了轨道角动量的两个量子数[9]。他的弟子泡利引入了自旋和不相容原理[10],最终奠定了可以解释元素周期的电子壳层模型。不相容原理导致了费米—狄拉克统计分布 (参见Box 2)。泡利将其应用到自由电子气中,解释了基于电子自旋的弱顺磁现像[11]。索末菲则计算了电子比热,发现它比经典统计中能量均分定律所预言的小了很多。
BOX 2
麦克斯韦—玻尔兹曼分布与费米—狄拉克分布
导体理论从经典向半经典迈进的标志即是费米—狄拉克分布对经典的麦克斯韦—玻尔兹曼分布的替代。在经典力学框架下,当我们考虑大量粒子相互作用达到平衡态时,拥有特定能量的粒子的占比即由如下麦克斯韦—玻尔兹曼分布给出:
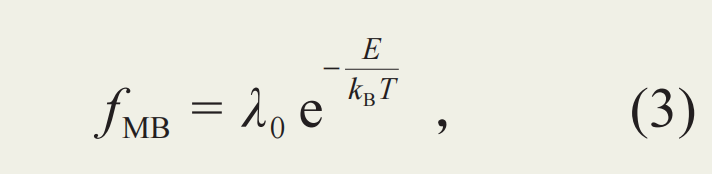
其中,E 为粒子能量,kBT 为玻尔兹曼常量,T为体系温度,λ0为系数。在最初由麦克斯韦所获得的分布函数中E仅包含动能,而玻尔兹曼将其推广到更为一般的能量。以能量为横轴,占有率为纵轴,我们能画出相应的概率分布图 (图1(a))。可以看出,当温度较低时,麦克斯韦—玻尔兹曼分布拥有窄而尖锐的、靠近零点的峰值。对于某一特定态而言,可以有多个粒子占据。
与之形成鲜明对比的费米—狄拉克分布是量子统计分布的一种。它适用于自旋为半整数的粒子(比如自旋为1/2的电子)。其表达式如下:
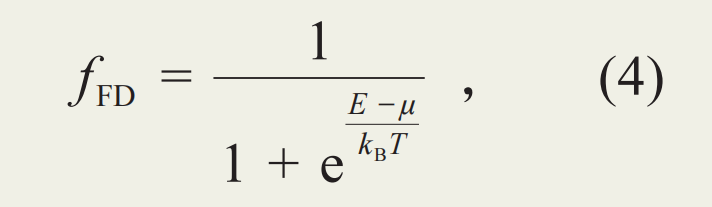
用以描述具有能量E的某一特定能态的占有概率。费米—狄拉克分布 (图1(b)) 明显不同于麦克斯韦—玻尔兹曼分布:特定量子态的占有概率不会超过1;当温度变为零 (绝对零度) 时,对于能量比μ小的态,其占有率为1,而对于能量比μ大的态,占有率为0。故能量μ代表了在零温下粒子能够填充的最高能量,称为费米能。在有限温度时,能量很低或很高的能态占有率和零温情况类似,但是费米能附近kBT大小的能量区间内,量子态的占有率明显不同于零温情形:存在从0到1的占有率的过渡。
我们可以通过泡利对顺磁磁化率的解释来形象化地看出二者的差别。由费米—狄拉克分布所得磁化率χFD与麦克斯韦—玻尔兹曼分布所得磁化率χMB具有如下比值:χFD/χMB∝kBT/E0。由此可见,在低温下,量子统计所给的值相较于经典统计的值大大缩小。根据费米—狄拉克统计,在低温下,能量低于费米能的能态几乎被完全占据。在弱磁场下,大部分量子态的分布几乎不变——产生显著变化的仅有费米能附近明显不被完全占据的区域 (图1(b)),也即kBT大小的能量区间。此区间相对于总能量的占比即为kBT/μ。这粗略给出了量子统计的磁化率相对于经典统计值的缩小比例。
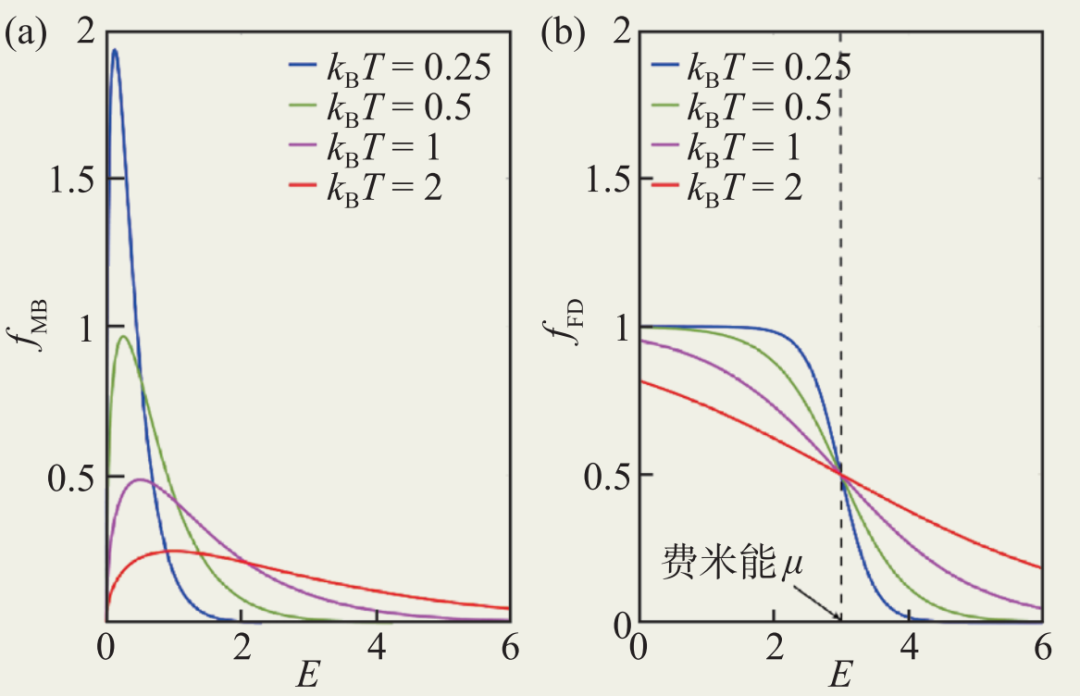
图1 不同温度下的麦克斯韦—玻尔兹曼分布(a)与费米—狄拉克分布(b)
现在我们已熟知,导体中的电子气高度简并。在零温下,电子会像倒入盆子里的水那样从最低能量处填起,直到某个被称为费米能的地方——它上面的量子能级不被占据。依据金属中的电子密度,这个费米能比常温对应的热涨落能量高出两三个数量级。故而金属中的电子在常温下仍然非常冷:大量深埋于费米能之下的电子不受影响,只有紧邻费米能的少数电子可被激发。
量子统计需要用到量子态的计数,但宏观体积内电子态的能级非常密集,故泡利和索末菲在计算过程中做了连续化处理。根据量子波动力学,自由电子可用平面波表示,其能量和动量分别正比于频率和波矢,比例系数就是普朗克常数。由于波函数受边界条件的限制,波矢只能取一些分立的值,类似两端固定的琴弦上的驻波。平均来看,单位空间和动量体积内量子态的数目反比于普朗克常数的三次方。这正好对应到经典统计力学中用相空间体积来度量微观状态的数目。量子波动力学把那个曾经语焉不详的经典统计测度给彻底明确了下来。
在输运问题上,索末菲等人一方面仍然沿用了电子的经典粒子图像,另一方面从费米—狄拉克分布出发利用弛豫时间近似得到非平衡分布[12,13]。这个由量子统计改造过的自由电子模型明确了传导电子来自费米能附近,可以更好地描述金属的热传导和热电效应。但是,电子的粒子图像仍面临一个巨大的困难:由金属导体的电阻推断出来的平均自由程可以远大于原子间距,好像在贡献出电子后,周期排布的正离子对电子就不再起作用了。这完全不符合人们之前设想的摩擦力的起源。
02
布洛赫电子模型
新的突破还有待于索末菲的徒孙,师从海森伯 (Werner Heisenberg) 的一位年轻人布洛赫。他在博士论文中把刚从薛定谔那里学到的量子波动方程应用到处于晶体材料周期势场中的电子[14]。他惊喜地发现,能量本征波函数仍类似自由状态下的平面波,只是振幅在空间中获得了周期性调制。这个发现为解决平均自由程过大的问题扫平了障碍,因为周期排布的离子实阻挡不了具有这种波函数的电子在晶体中的运动。这种准平面波后来被称为布洛赫波。它的波矢对应了一种新型的动量 (为了简便,以下仍称为动量),定义在一个有限无界、具有循环结构的区域 (布里渊区)。能谱也因之呈现为此区域中的一条条能带 (参见Box 3)。
BOX 3
布洛赫理论与波包
在1928年,布洛赫发表了著名的“晶格中电子的量子力学”一文,推动固体理论的研究迈入量子时代。在一维情况下,他考虑晶格中电子具有如下哈密顿量: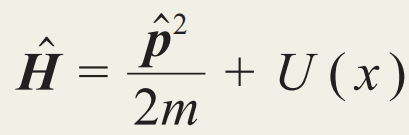 。不同于自由电子,电子感受到的势场U(x)是由各个离子产生的势场之和(图2)。由于离子排布的周期性,U(x)继承了此性质:U(x+a)=U(x)。其中,a为相邻离子之间的间隔。布洛赫发现,在周期势场之中,电子本征波函数是一种被调幅的平面波,即布洛赫波:
。不同于自由电子,电子感受到的势场U(x)是由各个离子产生的势场之和(图2)。由于离子排布的周期性,U(x)继承了此性质:U(x+a)=U(x)。其中,a为相邻离子之间的间隔。布洛赫发现,在周期势场之中,电子本征波函数是一种被调幅的平面波,即布洛赫波:
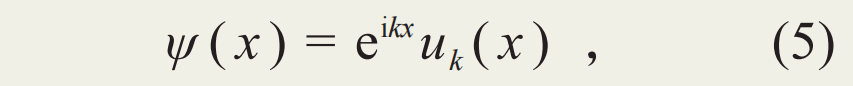
其中,振幅u(x)具有与势场相同的周期性:uk(x+a)=uk(x)。这里需特别指出的是,不同于自由电子的平面波波函数,此处波函数的指标k不完全是电子的动量,而是一种晶格动量。它的取值不再是负无穷到正无穷,而是如布里渊所发现的,处于一个有限大小的布里渊区之中。对于一维晶格,此布里渊区即为[-π/a,π/a),其左右端点等价。
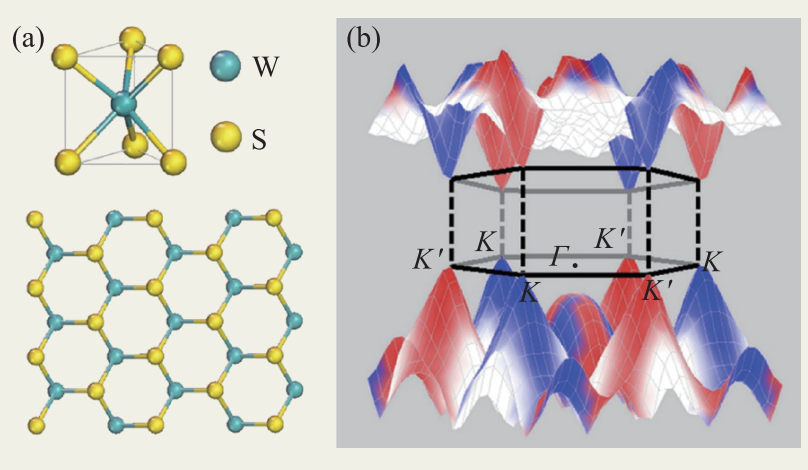
图2 单层二硫化钨(WS2)晶格与二维能带 (a)二硫化钨晶格的单元格构型(上)及俯视图(下);(b)二维能带以及晶格动量所在的布里渊区(图(a)摘自Ye Y et al. Nature Photonics,2015,9:733;图(b)摘自Bussolotti F et al. Nano Futures,2018,2:032001)
与每个本征态相应的本征值可组成能带的结构。能带的形成与分子中的能级十分相似 (图3)。当晶格中相邻离子之间的距离非常远的时候,晶格实际上是没有相互作用的原子的集合。此时电子的能量本征值就是原子中的电子能级。在相邻离子间的距离慢慢拉近的过程中,相邻原子中的电子波函数的电子云重叠逐渐变得显著,使得原子能级发生共价键型耦合,形成成键态 (能级降低) 与反键态 (能级升高)。换言之,在晶体中,原子能级从单一值弥散至一个能量区间,而这些能量在动量空间的进一步排布即形成能带 (图2,图3)。
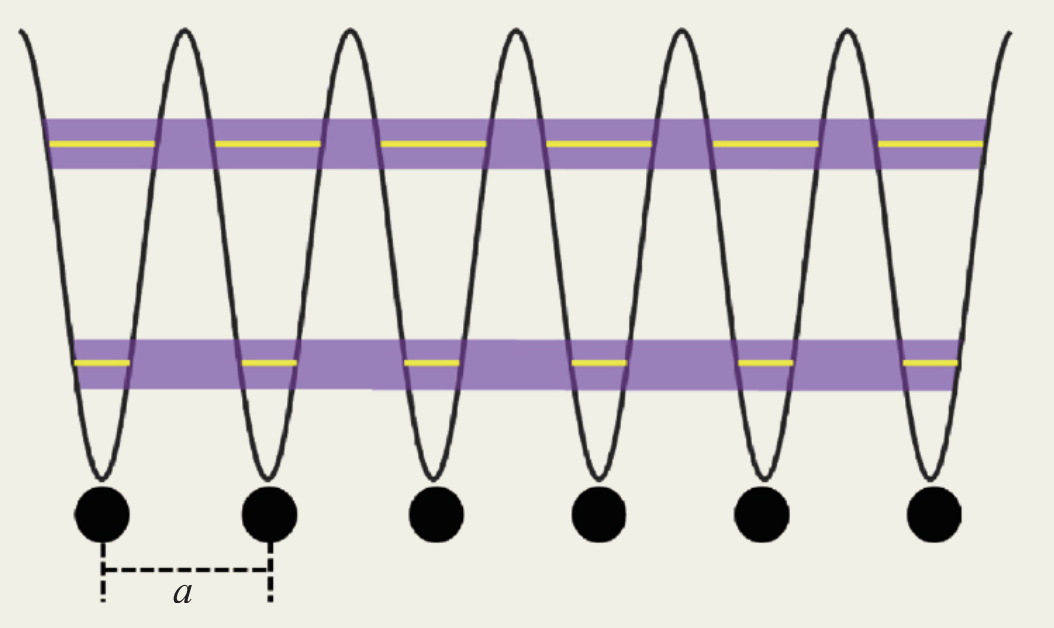
图3 固体中电子感受到的周期势场与能带。黄线展示每个原子中的电子能级,其初始值对于不同位置的原子相同。紫色区域则为不同原子的电子云重叠导致原子能级弥散而成的能带
布洛赫也考虑了电子在电场下的加速行为。在一般的三维情况下,他以布洛赫态线性组合的方式构造了波包:
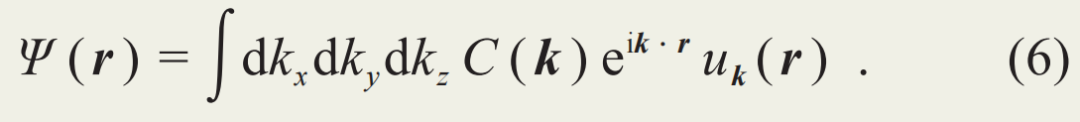
波包形式可被进一步限制,使其在动量空间局域在某个中心点kc附近。根据不确定性原理,波包态在实空间则可大为展宽 (图4):波包虽有实空间的中心点rc,但其宽度可远大于离子间距 (这是组成波包的布洛赫态所感受的周期) 。在考虑电子的响应性质时,我们往往需要加某些外力,同时要求这些力足够小,使得其能探测而不是改变电子的本征性质。这时,和外力对应的外势会在空间变化。为合理使用波包描述电子运动,我们需要进一步要求其实空间展宽远小于外势的特征变化尺度 (图4)。在电场E的作用下,布洛赫在量子力学框架下发现了这样的受力方程:

电子的速度方程则变为

除了这里的动量是取有限值的晶格动量之外,这组动力学方程与经典情形 (方程(1)和(2)) 完全一致。后来,琼斯和齐纳发现,磁场也可用相似的方法加入进来,相应的受力方程仍然保持与经典情形一致:
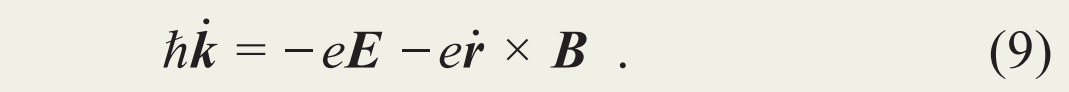
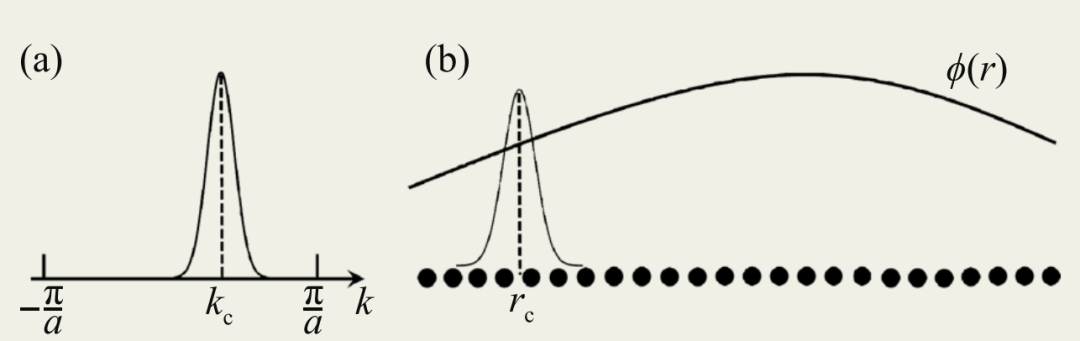
图4 波包在动量空间(a)与实空间(b)的分布((b)图中黑色小球代表原子位置)
一个能带里的布洛赫波所对应的粒子是什么样子呢?我们可以将某个动量附近的布洛赫波线性叠加而获得一个动量相对确定 (相比布里渊区的大小而言) 的波包 (参见Box 3)。而如果我们将视野放宽到远远大于原子间隔的尺度,就会发现其在空间上也相对局域,从而具有相对确定的位置。这种有明确位置与动量的波包即可展现出布洛赫波的粒子性。其群速度即是动量中心处布洛赫态的速度期望,等于其能量对动量的偏导。这个速度在能带的下部随动量增长,但到了上部就反了过来,就好像质量从正变为负。
在一般强度的电磁场下,规范势场对薛定谔方程的微扰在空间变化极其缓慢,可以在布洛赫波包的空间宽度上变化无几。利用这个条件,布洛赫发现波包在电场作用下动量匀速变化,如同自由电子一般。之后,这个结果又被琼斯 (Herbert Jones) 和齐纳 (Clarence Zener) 推广,在电场力之外添上了磁场的洛伦兹力[15]。这些发现使能带中电子的粒子图像重获新生:我们只需将自由电子的能动量关系换成布里渊区上的能带函数,然后隐去晶格势场的存在。由此获得的布洛赫电子在电磁场下遵循原先的动力学规律。
基于布洛赫电子的粒子图像和弛豫时间近似,索末菲等人的电子理论稍作修改即可继续应用到实际金属材料中去。布洛赫的理论表明,造成电子散射的原因只能来源于晶体周期性的破坏,比如杂质缺陷以及原子振动。布洛赫在他的博士论文中还具体考虑了后者对电子的散射,成功解释了电阻率随温度而上升的趋势。在高温区,晶格振动满足经典的能量均分定律,强度随温度线性增长,其对电子的散射也随之增强,最终导致电阻率的升高。在低温区,利用德拜 (Peter Debye) 当时刚刚得到的声子量子化成果,布洛赫还预言了著名的温度五次方的电阻行为。因为杂质散射会导致零温时有限的电阻,他的这个预言后来在非常纯净的晶体中才被证实。
如果没有散射,电子动量在电场下的匀速增长使得布洛赫电子在一个能带里周而复始的运动,这被称为布洛赫振荡。这种直流转交流的理想状态很难在固体材料中实现,因为弛豫时间往往远小于这种振荡的周期。后来江崎 (Leo Esaki) 发明了超晶格系统,让布洛赫振荡周期大大缩小,从而首次观察到了这个现象[16]。又过了很多年,布洛赫振荡终于在光晶格中的冷原子体系被完美地实现,成为一种精确测量重力加速度的方法[17]。
布洛赫理论还可以描绘绝缘体和半导体。威尔逊 (Alan Wilson) 注意到,如果一个能带被电子整个填满,则总电流为零;在电场作用下,动量在能带中循环,并不改变能带的填充,总电流仍然为零[18,19]。这样,如果所有的能带要么空着要么完全填充,这个材料就是绝缘体。这个情况就像原子的量子模型里填满了的壳层表现出惰性一般。但是,以后我们会讲到,上述考虑忽略了布洛赫电子的拓扑几何效应,动量的循环其实可以导致垂直于电场方向一个量子化的反常霍尔电流。
纯净完美的半导体在零温下也是绝缘体。但它的满带和空带之间的能隙比较小,容易在室温和掺杂的情况下使得空带底部的量子态被占据,或者满带顶部的量子态空出。其中后者被称为空穴,等效于满带顶部被电荷为正的粒子占据。这些粒子的行为如同自由电子一般,但其有效质量决定于能带的曲率。有趣的是,由于空穴带正电,其相应的霍尔效应的符号与电子的相反,这完美解释了索末菲理论留下的一个重大疑惑。
03
量子多体作用
电子的粒子观还要经受一场量子多体作用的锤炼。简单地说,电子除了感受到原子核的库仑引力外,还受到电子之间的库仑斥力。晶格的周期结构和其他自由度的秩序都是这些库仑作用在量子力学中表现的结果。严格来说,布洛赫电子只是某种平均场意义下的存在。
在极端情况下,比如超导和莫特绝缘体中,电子会以一种焕然一新的样子呈现。在前者,电子由于某种吸引作用而配对为玻色子,并进一步凝聚到超导电性和完全抗磁的状态。在后者,由于相对强烈的库仑排斥,电子的电荷被限制在一个个元胞里,相邻元胞的自旋相反排列,使得系统呈现绝缘反铁磁序。还有一类体系表现出拓扑序,包括近期观察到的反常分数量子霍尔状态,其中的元激发以分数电荷的形态出现,并且表现出不同于费米子和玻色子的量子统计。
本文不打算讨论这种强关联系统,而是把目光集中在通常遇到的固体物相上,其电子的多体量子基态可以看成对各布洛赫能带自下而上的填充。早期多体物理研究的一个关键人物是斯莱特 (John Slater),他从美国到欧洲从事博士后研究。他曾推广了哈特里 (Douglas Hartree) 的自洽平均场方法,把自旋和轨道态一起纳入到一个后来以他命名的多体行列式波函数,定量地解释了原子的精细结构[20]。遇到海森伯和布洛赫以后,他就着手比较基于他们用的束缚态和延展态的多体波函数,发现后者在一般的金属中更加适用[21]。
对多体波函数的进一步研究催生了现代固体电子结构的第一性原理计算。基于布洛赫态的图像,密度泛函理论中的科恩—沈吕九方程也具有薛定谔方程的形式,只是每个电子感受到的势场由一套普适的自洽方程得出。这种计算可以精确地给出固体的结合能,预言晶体的微观几何结构和材料的宏观弹性等。
对于金属,受朗道费米液体理论的支撑,由第一性原理计算得到的费米面结构可以通过德哈斯—范阿尔芬效应进行严格检验,并应用到各种线性响应问题里。对于能带绝缘体来说,第一性原理计算也可以给出很好的基态性质。但涉及到半导体激发态的描述,比如能隙和激子结合能等,第一性原理方法还需要一些多体微扰修正。
关于铁磁性,早期曾有海森伯的局域磁矩和布洛赫的巡游磁矩两种对立的观点[22,23]。现代的自旋密度泛函理论基于后者,可以精确地预言铁、钴、镍等过渡金属的基态磁化强度。海森伯的自旋耦合模型仍然流行于教科书和科学研究中,因为它更方便于描述自旋波激发和相变,但其中的耦合系数还是要结合线性响应理论以及第一性原理计算来量化。
自旋波激发是一种典型的玻色子,它描述了系统对固定磁序比如铁磁序的偏离模式。它们的热激发会让长程铁磁序在三维情况下以温度的3/2次方形式减小而在低维情况下完全丧失。同样,声子 (晶格振动的玻色量子) 的热激发也可以对晶格的平移对称序产生类似的影响。在远大于原子的尺度上,这些涌现出来的玻色子往往以经典的粒子形态表现,它们对外界条件的响应也可以参照电子的情形来处理。
04
单带量子理论
材料的磁性一直是推动固体理论发展的重要课题。当考虑量子物理中的自旋概念时,泡利已证明自由电子气可展现出顺磁性。之后,朗道 (Lev Landau) 考虑了磁场对轨道波函数的作用,解出一系列分立的能级 (朗道能级),并在弱场极限下发现了自由电子气的抗磁性[24]。这让人们大吃一惊,因为在1911年前后玻尔 (Niels Bohr) 等人曾证明,在平衡分布下,经典的轨道运动不会给出任何磁性[25]。他们的论述对于费米—狄拉克统计也成立。朗道的工作引起派尔斯 (Rudolf Peierls) 好奇:对于一个能带中的布洛赫电子,该如何把轨道量子效应找回来呢?
布洛赫求解他的波函数时采取了紧束缚近似:把各个原子上的波函数作线性叠加,通过量子隧穿把原子能级展宽成能带。派尔斯注意到,即使忽略弱磁场对原子波函数的修正,磁矢势仍然会给各原子上的波函数赋予不同的相位,让原子之间的隧穿系数多出相应的相位差[26]。这使得紧束缚哈密顿量的动量算符产生一个正比于磁矢势的移动。这就是著名的派尔斯替换,而替换后的动量在垂直于磁场的两个方向上不再对易。多年后,索利斯等人研究量子霍尔效应时用到的一个哈密顿量模型也是这样得到的。
通过对自由能的微扰计算,派尔斯得到了布洛赫电子气的抗磁系数,还在低温区发现了磁化强度的振荡行为,开启了对德哈斯—范阿尔芬效应的解释[27]。在自由电子情形时,这个振荡对应于一个个朗道能级穿过费米面。多年以后,昂萨格 (Lars Onsager) 通过玻尔—索末菲量子化方法,把这个振荡现象归结为布洛赫电子回旋运动映射在动量空间中的轨迹所围面积的量子化,使之成为研究费米面几何形状的指导方针[28]。
1937年,瓦尼尔 (Gregory Wannier) 在研究半导体激子的过程中,在缓慢变化的外标势里对固定能带作了量子化处理[29]。斯莱特把这个方法总结为瓦尼尔定理:有效哈密顿量就是能带函数加外势场,前者里的动量与后者里的位置成为一对正则变量,满足量子对易关系。教科书里讲到的类似于氢原子能级的激子能谱和杂质能级就是根据这种有效哈密顿量得到的。
瓦尼尔在研究过程中还发展出了他著名的瓦尼尔函数,用它可以把能带中的布洛赫波函数做傅里叶展开。这类似于紧束缚方法中用到的原子波函数,但不再有尾部重叠,而总是正交归一。1951年,拉廷格 (Joaquin Luttinger) 利用瓦尼尔函数,把前面讲到的派尔斯替换推广到了超出紧束缚的情形[30]。这样,瓦尼尔定理加上派尔斯替换,我们就得到了一般能带在电磁场下的有效量子理论。
上面讲到,在不受散射的时候,电子可在电场的作用下在能带里周而复始地做布洛赫振荡。瓦尼尔发现,这种振荡对应的本征定态是一组阶梯 (斯塔克阶梯) ,具有等间距的能级和局域在每个元胞附近的波函数[31]。有意思的是,这种定态波函数也是具有最小宽度的瓦尼尔函数。多年以后,斯塔克阶梯在光晶格里的冷原子系统中被清晰地观察到[32]。
但是,下面我们就会讲到,由于布洛赫能带的拓扑几何效应,这种基于瓦尼尔函数的单带量子理论并不总是成立。比如,索利斯证明,当一个能带的陈数非零的时候,此能带的局域瓦尼尔函数就不再存在。上述拉廷格的工作之后,科恩 (Walter Kohn) 等人发展了一套基于正则变换的方法来获得电子的有效哈密顿量[33],不再依赖局域瓦尼尔函数,而且此方法也可以推广到电磁场的高阶,但他们的推导过程和结果颇为繁复,没有得到广泛应用。究其原因,那时还缺乏对于布洛赫态的拓扑几何性质的明确认识。
05
拓扑几何效应
1980年,冯·克利青 (Klaus von Klitzing) 发现了二维电子气在强磁场下的霍尔电阻呈现出一系列由基本物理常数 (普朗克常数和电子电荷) 决定的、量子化的平台[34]。为了解释这个量子霍尔效应,索利斯等人研究了二维布洛赫电子在强磁场中的子能带,发现每个满子带贡献一个量子化的横向电导[35]。他们的结果揭示了一种物理背景下的拓扑陈数,对于布洛赫能带具有普适性,也可以推广至无序和多体作用的情形。这个理论拉开了凝聚态物理对布洛赫电子拓扑和几何性质研究的序幕,其预言的量子反常霍尔效应后来被薛其坤团队证实[36],也推动了对各类拓扑材料风起云涌般的研究热潮。为此,索利斯获得2016年诺贝尔物理学奖。
拓扑陈数与布洛赫态在动量空间的贝里几何相位有密切联系:它等于相位的密度 (即贝里曲率) 在布里渊区的积分 (参见Box 4)。对布洛赫波包的仔细分析表明,电子除了我们熟悉的群速度以外,在外力下还有一个正比于贝里曲率的反常速度[37—39]。找回这一项后,电子的运动方程看上去更加对称:反常速度具有类似洛伦兹力的形式,而贝里曲率就如同动量空间的“磁场”。这个“磁场”使得电子的运动轨迹发生垂直于外力方向的横向偏移,从而导致一个反常霍尔效应。这在满带情况下正好对应上面提到的,以陈数描述的拓扑量子化结果。
BOX 4
贝里曲率与半经典理论
在1994年至1999年的时间中,张明哲、牛谦、G. Sundaram通过变分的方法构造出完整的半经典理论框架。他们考虑了如下的拉格朗日量:
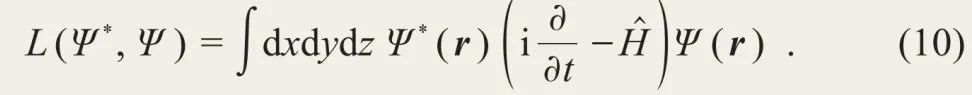
令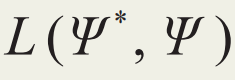 对波函数做变分可给出完整的薛定谔方程。从这个意义上讲,它是完备且精确的。半经典理论则始于对波函数形式的限制。当如前所述限制波包在动量空间和实空间的形式之后,张明哲等发现,拉格朗日量中蕴含量子行为的波函数消失了,取而代之的是经典的波包位置和动量,及其时间导数:
对波函数做变分可给出完整的薛定谔方程。从这个意义上讲,它是完备且精确的。半经典理论则始于对波函数形式的限制。当如前所述限制波包在动量空间和实空间的形式之后,张明哲等发现,拉格朗日量中蕴含量子行为的波函数消失了,取而代之的是经典的波包位置和动量,及其时间导数: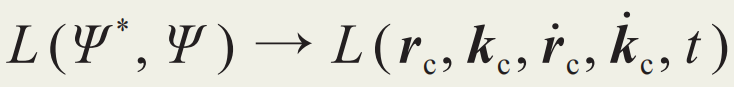 。我们仍需注意,虽然此拉格朗日量只包含经典力学量,但它仍与经典力学中的拉氏量不同:在经典力学中,拉氏量只与位置、速度、时间相关,而这里又多了晶格动量与其时间导数。由此拉氏量推出的半经典动力学方程如下:
。我们仍需注意,虽然此拉格朗日量只包含经典力学量,但它仍与经典力学中的拉氏量不同:在经典力学中,拉氏量只与位置、速度、时间相关,而这里又多了晶格动量与其时间导数。由此拉氏量推出的半经典动力学方程如下:
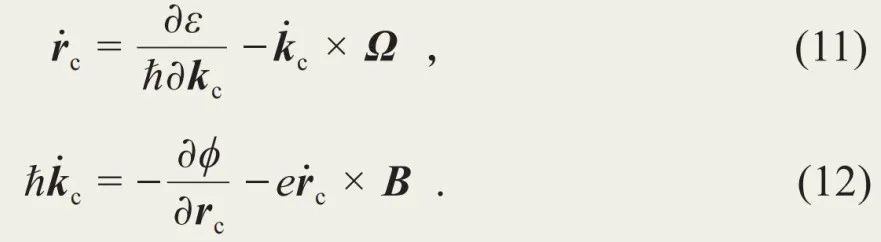
对比经典的电子运动方程(方程(1)和(2),方程(7)和(8)),这组动力学方程明显不同:虽然电子受力仍是洛伦兹力,但是电子的速度获得一个新的贡献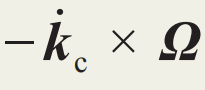 ,此即为反常速度。其中Ω称为贝里曲率,它反映了布洛赫态自身的几何性质。
,此即为反常速度。其中Ω称为贝里曲率,它反映了布洛赫态自身的几何性质。
贝里曲率的计算涉及到材料中的复杂能带结构。其常用的计算表达式如下:
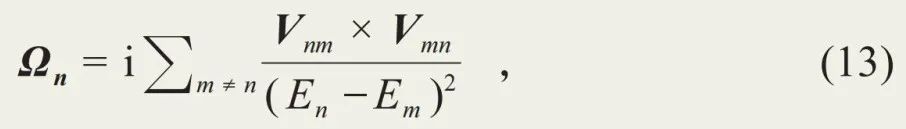
其中,En是电子的本征能量,Vnm是速度算符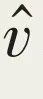 在第n条和m条能带的布洛赫态下的矩阵元。方程(13)表明,特定能带上的贝里曲率的实际计算需要其他能带的布洛赫态参与。这里,我们需强调指出,虽然贝里曲率也可由单一布洛赫态的贝里联络的旋度给出,但由于贝里联络与规范选择相关,此关系不适于贝里曲率的数值计算。
在第n条和m条能带的布洛赫态下的矩阵元。方程(13)表明,特定能带上的贝里曲率的实际计算需要其他能带的布洛赫态参与。这里,我们需强调指出,虽然贝里曲率也可由单一布洛赫态的贝里联络的旋度给出,但由于贝里联络与规范选择相关,此关系不适于贝里曲率的数值计算。
方程(11)还有另一个与经典速度方程不同的地方:第一项中的能量不是简单的能带能量,而是包含了源于轨道运动的轨道磁矩与磁场的耦合,也即ε=ε0-B⋅m;而在经典力学中,体系能量在外磁场下没有变化。如果用波包的语言看,这个轨道磁矩m实际代表了波包绕着自己质心的自转。前文所提的贝里曲率则代表了波包质心的公转。
如果进一步对比速度方程与受力方程,我们可发现,二者具有相似的结构:在把位置替换成动量,以及势能替换成动能之后,受力方程大致可变为速度方程的形式。这种相似性提示我们可以将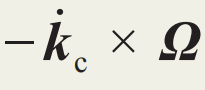 视为动量空间的“洛伦兹力”,而将Ω视为动量空间的“磁场”。实际上,Ω不仅具有和磁场相似的时空变换性质,甚至可具有相同的动力学效果:像磁场一样,贝里曲率也可以使电子的运动轨迹发生横向偏转(图5)。此即为著名的反常霍尔效应。其产生的电流与电场垂直,也即J=E×σ,而电导率可写为
视为动量空间的“洛伦兹力”,而将Ω视为动量空间的“磁场”。实际上,Ω不仅具有和磁场相似的时空变换性质,甚至可具有相同的动力学效果:像磁场一样,贝里曲率也可以使电子的运动轨迹发生横向偏转(图5)。此即为著名的反常霍尔效应。其产生的电流与电场垂直,也即J=E×σ,而电导率可写为
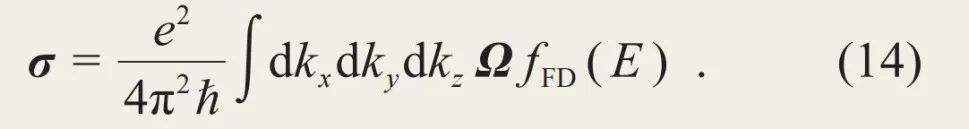
对于费米能位于能带中的二维半导体,上述反常霍尔电导只能取分立的量子化的值 (量子霍尔效应)。这是因为在闭合的布里渊区中贝里曲率的积分是量子化的:
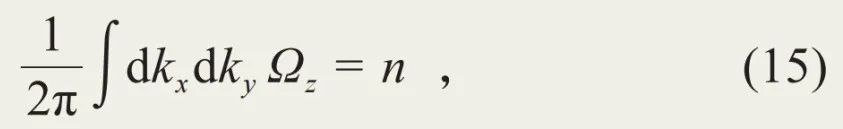
其中n取整数。
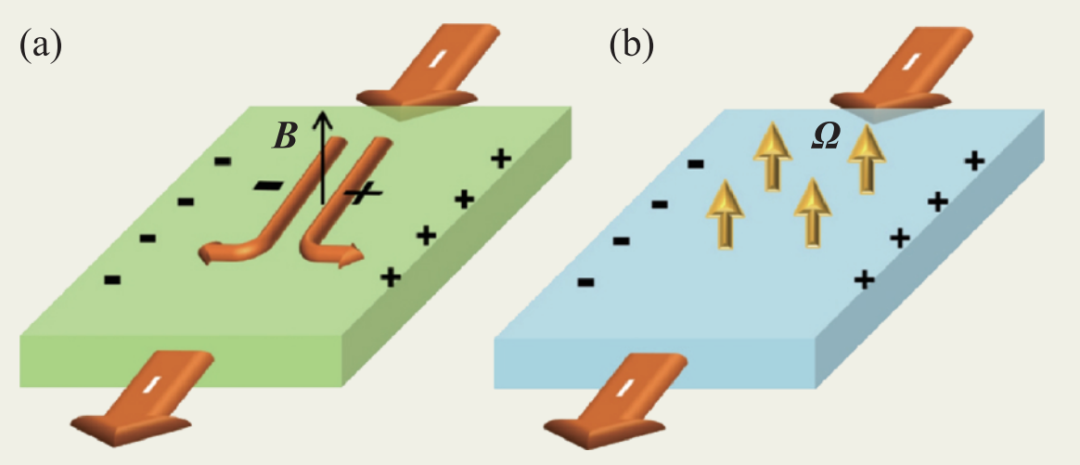
图5 霍尔效应(a)与反常霍尔效应(b)。图中的电流由电场驱动产生,而电子运动轨迹的横向偏转分别源于磁场和贝里曲率(图片摘自Chang C Z,Li M. J. Phys.:Condens. Matter,2016,28:123002)
对于时空上缓变的更为一般的微扰,布洛赫电子的响应会牵涉到贝里曲率在相空间和时间域中更多的分量[40]。比如,除了上面讲到的不同动量指标间的分量,还有动量和时间之间的绝热速度分量,有四维时空不同指标间的分量,以及动量和位置之间类似广义普朗克常数的分量。这些方方面面的贝里曲率在材料研究中都有着广泛的应用。
运动方程中用到的电子的能量等于局域近似下的能带值加上一些梯度项[39]。后者正比于某些物理量的偶极矩,可以用布洛赫函数计算,是布洛赫电子内禀信息的重要组成部分。经常用到的电子轨道磁矩就是一个例子,它刻画了电子能量在磁场中的线性移动。固体中电子磁矩的g因子和谷电子的磁矩都源于此。甚至电子自旋的玻尔磁子也可以认为来自于狄拉克方程能带中的速度偶极矩[41]。
上述电子的运动方程适用于非简并的能带,要求外力不足以造成不同能带间的齐纳跃迁。对于简并或近乎简并的能带 (经常发生在有关自旋的问题上),就需要用几率振幅来刻画电子在不同能带间的转移[42]。电子运动方程中有关的物理量就变成了矩阵,即非阿贝尔形式,再加上一个联立的几率振幅所满足的薛定谔方程。
由于贝里曲率的作用,布洛赫电子的运动方程不再是正则的哈密顿形式。关于相空间体积不随时间演变的刘维尔定理不再成立。为了使相空间量子态的数目守恒,以前从泡利和索末菲开始用到的态密度必须做出修改[43]。通过将实际的运动方程做换元变为正则形式后发现,电子的物理动量和位置相对于正则的动量和位置都有平移。这引发了对派尔斯替换的修正,也意外地揭示了简并能带中自旋轨道耦合的本源。
像布洛赫能带一样,第一性原理计算也可以给出贝里曲率和运动方程中的其他参数。这不仅可以给出绝缘体的拓扑陈数,也使人们可以结合费米—狄拉克分布,对实际金属和半导体材料的各种内禀性质,包括轨道磁化和反常霍尔效应,展开系统研究。近二十年来,人们在这方面取得了瞩目的成就。另外,上述布洛赫电子的运动方程也可以纳入玻尔兹曼散射理论框架,使对材料外禀输运性质的描述更为完善。
06
总结和展望
经典的牛顿粒子观在原子尺度上失效,但经过量子统计和波动力学的改造以及多体作用的锤炼,电子在更大的尺度上以新的粒子形态出现。其动量被局限在一个有限的区域内,能量则被隔离成一条条能带。当一条能带被电子占满,它就表现出惰性,不再参与导电和导热。金属中电子占据的最高能带里有个代表电子最高单体能量的费米面。常温下只有费米面附近少数电子可被激发,参与对外场的响应。
长期以来,固体中的布洛赫电子理论主要基于它们的能量,可以正确地给出材料的结合能、晶格结构和宏观弹性,以及对各种外场响应的基本图像。近四十年的研究实践表明,布洛赫态的贝里相位和相关的几何拓扑量也深深影响着电子的行为。本文简单回顾了贝里曲率如何修改电子的运动方程及其基本性质。后续我们会做较为详细的背景说明,具体介绍这如何改变了人们对固体诸方面物理性质的理解和计算。
类似于电子,晶体中的其他粒子,比如上面提到的声子和磁子[44],也遵循类似的运动方程。对于超导体中的准粒子,序参量不仅可以决定它们的能谱,也可以影响到贝里曲率和相应的拓扑性质[45]。我们可预期,声子和磁子所对应的序参量也会有类似的效果。
当需要考虑高阶梯度的影响时,我们需要对运动方程作适当的调整,但仍可保留原来的形式[46]。比如,把局域近似下的布洛赫态微扰,考虑到外场梯度引起的其他量子态的一阶混入,贝里曲率就可以准确到一阶,而能量可以准确到二阶。这样得到的运动方程就可以用来计算二阶响应问题[47]。这在近年来也开始有很多应用。
当布洛赫态所赖以定义的周期性发生改变,比如材料的应变随时空缓慢变化,粒子的运动会感受到一种时空弯曲效应[48]。当空间的周期性扩展为时空上的周期性,布洛赫态被代替为弗洛凯—布洛赫态——一种振幅在时空上周期调制的平面波。相应粒子的能量和动量被限制在四维环面上,满足与布洛赫粒子形式类似但内涵更加丰富的运动方程[49]。当这种时空周期再叠加上一个缓慢的类似于时空应变的调制,运动方程就要修改成广义协变的形式,从而为实验室里探讨人造引力开辟了一条可能的道路[50]。
致 谢 本文在构思阶段收到李灿国和孙凤国的宝贵意见,基本成文后又收到金晓峰、沈顺清、虞跃、施郁、周建辉、吴从军等同仁的专业点评,这里一并表示感谢。
参考文献
[1] Ashcroft N W,Mermin N D. Solid State Physics. 北京:世界图书出版社,2004
[2] Wilson A H. The Theory of Metals. Cambridge University Press,1953
[3] Hoddeson L H,Baym G. Proc. R. Soc. Lond. A,1980,371:8
[4] Hoddeson L H,Baym G,Eckert M. Rev. Mod. Phys.,1987,59:287
[5] Thomson J J. The Electrician,1897,39:104
[6] Thomson J J. Philosophical Magazine,1897,44:293
[7] Drude P. Annalen der Physik,1900,1:566;3:369
[8] Lorentz H A. Proc. R. Acad. Amst.,1905,7:438,585,684
[9] Sommerfeld A. Annalen der Physik,1916,51:1
[10] Pauli W. Zeitschrift für Physik,1925,31:765
[11] Pauli W. Z. Phys.,1927,41:91
[12] Sommerfeld A. Naturwissenschaften,1927,15:825
[13] Sommerfeld A. Z. Phys.,1928,47:43
[14] Bloch F. Z. Phys.,1928,52:555
[15] Jones H,Zener C. Proc. Roy. Soc. A,1934,144:101
[16] Esaki L,Tsu R. IBM J. Res. Dev.,1970,14:61
[17] Ferrari G,Poli N,Sorrentino F et al. Phys. Rev. Lett.,2006,97:060402
[18] Wilson A H. Proc. R. Soc. London Ser. A,1931,133:458
[19] Wilson A H. Proc. R. Soc. London Ser. A,1931,134:277
[20] Slater J C. Phys. Rev.,1929,34:1293
[21] Slater J C. Phys. Rev.,1930,35:509
[22] Heisenberg W. Z. Phys.,1928,49:619
[23] Bloch F. Z. Phys.,1929,57:545
[24] Laudau L. Z. Phys.,1930,64:629
[25] Bohr N. Studier over Metallernes Elektronteori. Doctoral dissertation,Copenhagen:Thaning and Appel,1911
[26] Peierls R. Z. Phys.,1933,80:763
[27] Peierls R. Z. Phys.,1933,81:186
[28] Onsager L. London Edinbuigh Dublin Philos. Mag. J. Sci.,1952,43:1006
[29] Wannier G. Phys. Rev.,1937,52:191
[30] Luttinger J M. Phys. Rev.,1951,84:814
[31] Wannier G H. Elements of Solid State Theory. Cambridge University Press,1959
[32] Wilkinson S R,Bharucha C F,Madison K W et al. Phys. Rev. Lett.,1996,76:4512
[33] Kohn W. Phys. Rev.,1959,115:1460
[34] von Klitzing K,Dorda G,Pepper M. Phys. Rev. Lett.,1980,45:494
[35] Thouless D J,Kohmoto M,Nightingale M P et al. Phys. Rev. Lett.,1982,49:405
[36] Chang C Z et al. Science,2013,340:167
[37] Chang M C,Niu Q. Phys. Rev. B,1996,53:7010
[38] Chang M C,Niu Q. Phys. Rev. Lett.,1995,75:1348
[39] Sundaram G,Niu Q. Phys. Rev. B,1999,59:14915
[40] Xiao D,Chang M C,Niu Q. Rev. Mod. Phys.,2010,82:1959
[41] Chang M C,Niu Q. J. Phys.:Condens. Matt.,2008,20:193202
[42] Culcer D,Yao Y,Niu Q. Phys. Rev. B,2005,72:085110
[43] Xiao D,Shi J,Niu Q. Phys. Rev. Lett.,2005,95:137204
[44] Murakami R,Murakami S. Phys. Rev. Lett.,2011,106:197202
[45] Wang Z,Dong L,Xiao C et al. Phys. Rev. Lett.,2021,126:187001
[46] Gao Y,Yang S A,Niu Q. Phys. Rev. Lett.,2014,112:166601
[47] Gao Y,Yang S A,Niu Q. Phys. Rev. B,2015,91:214405
[48] Dong L,Niu Q. Phys. Rev. B,2018,98:115162
[49] Gao Q,Niu Q. Phys. Rev. Lett.,2021,127:036401
[50] Li A,Dong L,Niu Q. Geodynamics in spacetime crystal under slow perturbation and deformation. 2023,arXiv:2310.16918
本文经授权转载自微信公众号“中国物理学会期刊网”。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 