“数学无处不在”,这是数学圈子认可的;不过很遗憾,有时社会对数学的作用并不太认可。但实际上,正如笛卡尔所说,数学是最有效的一个工具。数学追求自身的逻辑体系,我们对待数学不要太苛刻,尤其要给做数学基础研究的人轻松平和的环境。
演讲 | 袁亚湘(中国科学院数学与系统科学研究院研究员)
数学的定义
仁者见仁,智者见智,数学的确有很多不同的定义,有趣的是每个人都可以选择自己喜欢的定义。

数学的多种定义
在中国,并不是自古就有“数学”这个词,古代有《九章算术》、《算学》等,但现在“数学”这个统一的名字,是1935年中国数学会的理事会决定的。
“数学”的英文Mathematics来自于希腊词根,Ma和ma在希腊文是μ和α,翻译成英文都是Ma。其实数学在希腊语意思是“学问的基础”,译成中文是“干什么就要学什么”。
数学不像艺术、体操、音乐,有些是不学自通的。比如湘西出了很多歌唱家像宋祖英、李谷一、张也,她们可能天生嗓子好,无师自通。但数学不行,一定要好好学习。
喜欢数学的小朋友们应该很开心,因为每年的3月14日是“国际数学日”,这不是数学工作者自封的,是2019年联合国科教文组织官方认定的,与国际劳动节、国际妇女节有同等地位。今年数学节主题是“Playing with Math”,中国数学会将其翻译成“游于数”,即“玩好数学”。为什么3月14号是数学节?因为π精确到小数点后两位是3.14。
从古至今数学家都对圆非常感兴趣,古希腊阿基米德通过研究内接多边形跟外切多边形的周长,估算圆周长度,即“割圆术”。中国古代割圆非常厉害,割圆术被中国的刘徽、祖冲之用到登峰造极。
圆周率在古代一直表述为“用它乘以直径就得到圆周长的量”。实际上最初用π这个记号,是英国一位数学教师William Jones,在他1706年出版的教材里首次用到。后来著名数学家欧拉在他的文章和教材里广泛使用,所以全世界统一用π来记圆周率。
关于π有很多有趣的公式,比如1减去1/3,再加上1/5,再减去1/7,即把所有奇数排起来,一个加一个减,依次往复,最后会越来越靠近π。精确到小数点后几百位太麻烦,但数学家利用高深的数学发明了一些奇怪的公式,可以求得非常快。比如下图倒数第二个公式,求一项就能精确到小数点后7位。
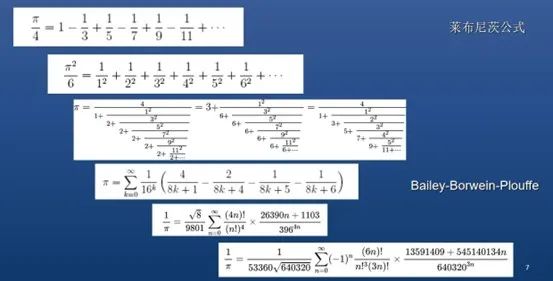
一些求π的公式
关于π的世界纪录,祖冲之在5世纪就算到了小数点后7位,保持世界纪录长达千年,所以中国古代数学还是很辉煌的。最近π已经算到了小数点后105万亿位了。
π有一个有待证明的有趣性质:把身份证号码输进去,在π里能找到,比如19210701是党的生日,精确在4400多万位就能找到这个数串。同样道理,输入共和国的生日19491001也能找到,但稍微难一点,在8200多万位。所以我经常开玩笑:π告诉我们,先有共产党后有新中国。当然一般来说,数串越长越难找。如果输入1314,很快就能在小数点后3902位找到,但如果在1314前面加520,就难多了,在200多万位才能找到。仿佛告诉我们:一生一世很容易,但要爱一个人一生一世还是挺难的。
数学的特点
下面扼要谈谈数学的几个特点。数学的第一个特点是“美”。大家可能觉得数学难,枯燥无味,跟美毫无关系。但几乎所有的数学家都认为数学是美的。大学里有一门课《泛函分析》,主要讲的是数学家巴拿赫的研究成果。巴拿赫说他用的数学是最美的。

关于数学的照片和插画
上图第一行中间的两张画,是西方文艺复兴时期几何教材的插画,插画作者是达·芬奇。伟大的画家达·芬奇为数学课本画插画,说明他也认为数学是美的。
“美”这个汉字是对称的,实际上美的其中一个特征就是对称,说明中国古代发明汉字的人很聪明。在数学里面对称随处可见,比如一些几何图形有对称轴,有2条的、4条的,圆有无数条对称轴。在代数上,一个多项式中X1跟X2的位置相同,同等重要,也是对称。
几何上有对称,代数上有对称,更重要的是,数学分析问题的思想也可以对称,在大学高等数学的“对偶函数”,包括《博弈论》里“利润最大,风险最小”,都是对称的。
数学还有一种美,是“比例美”。著名天文学家开普勒曾说过“几何上有两大美女,一是勾股定理,另外一个是黄金分割”。达·芬奇的画里大量用到黄金分割比例。希腊雅典的帕特农神庙也大量出现黄金分割比例,比如神庙长和高的比,柱子顶锥形两部分的比,屋檐跟三角屋顶比,都是黄金分割比例。在《几何原本》里,已经对黄金分割比例进行了定义,可见古希腊的几何非常发达,所以古希腊的建筑师就是数学家。
数学还有一个美是“简洁”。美好的东西一般都不会太复杂,举四个例子:一是欧拉公式,是把欧拉常数,虚数i,也就是-1的开方,还有π,还有+1、=、0有机地结合起来。二是欧拉的点线面公式,凸多面体顶点的个数跟棱边的个数、面的个数,也是简单的方程联系在一起。三是牛顿定律,在物理里是最本质的刻画运动的规律,是用简单的F=ma描述。四是麦克斯韦方程。电磁的关系能够用这四个简单的方程描述出来,非常简洁,但非常有用。
数学的美还有一点是非常神奇。比如勾股定理很神奇,32加42等于52,这样的勾股数有很多。把勾股定理的平方换成大于2的整数就没有解,这就是“费马大定理”。还有哥德巴赫猜想,大于4的偶数都可以写成2个素数的和,比如12可以写成5加7,14可以写成7加7,即每个偶数都可以写成两个素数之和,很神奇。
数学的美还在于它非常干净。钻石很漂亮,但钻石一定不能有瑕疵。约翰·洛克是法国非常著名的社会活动家、思想家,美国的《独立宣言》、《宪法》有很多思想和条文,甚至都是引用约翰·洛克的原文。这么伟大的思想家,竟是用钻石来比喻数学的。
数学的美还有一个特点是“素颜美”。不同于现在网络美女常用的瘦脸、美颜,数学的美真的是素颜美,罗素就是用雕塑来比喻数学。美好的东西千千万万,音乐靠美妙的声音让我们的耳朵享受听觉之美;油画用漂亮的色彩让我们的眼睛感受视觉之美;雕塑则不同,它不需要华丽的妆点,它就是素颜美,数学的美也具有素颜美的特点。
数学的第二个特点是“真”。爱因斯坦说:纯数学是逻辑思维的诗歌。爱因斯坦是著名的物理学家,数学家都很崇拜物理学家,因为物理学家有着优秀的刻画物理世界的思想,是我们意想不到的。爱因斯坦是3月14号数学节这天出生的,另一位著名物理学家霍金是3月14号去世的,可见很多物理学家跟数学的联系密切。
著名数学家韦伊,把数学证明的严格上升到道德的高度,所以小朋友们做数学题,一定要非常严谨,非常严格,按道德的标准来要求自己。如果不严谨、不严格,就好像没脸出去见人了。
数学还是揭露真理的,引用英国一位大主教的话:“数学就是揭露真正的真理,是求真的”。数学很注重公理化,在某种意义上它有A结果,是因为有B结果,有B结果是因为有C结果,一直推理下去。就像我们在二楼不掉到一楼是因为有楼支撑着,整个楼房不往下掉是因为有地基支撑着,地基不往下沉是因为有地壳支撑。这么一直推理下去,最底层的就是公理。因此数学是建立在一些公理基础上的,比如欧式几何有五条公理,比如过直线外一点只能做一条平行线,谁也证明不了,只能假定它是公理并承认它。
数学的第三个特点是“有趣”。著名的华人数学家陈省身,在2002年中国召开的国际数学大会题写了“数学好玩”。这是上半句,下半句是“要玩好数学”。所以学数学就像玩游戏,一定要好好玩,才能玩好。
数学为什么好玩?比如同学们都学过等差数列、等比数列,挺好玩的。还有一些数可以排成一个阵,中国古代就有《河图》、《洛书》,把1~9填在“田”字里,横竖加起来都等于15,也很好玩。这种数阵很多,包括数独,也是某种特殊性质的数方。还有,3的倍数,它的各个位上的数加起来也是3的倍数;能被9整除的数,它的各个位数加起来也能被9整除。
还有一些特殊的数,比如“同余数”:直角三角形的面积如果是整数,且每条边都是有理数,这个面积就是同余数。比如勾股定理32加42等于52,3、4、5边长的直角三角形面积等于6,6是同余数。同样道理,5、6、7都是同余数。但是1、2、3都不是同余数,即不存在一个直角三角形,面积正好等于1,且每条边都是有理数。
再例如“亲和数”:一个数的约数加起来等于另外一个数,另外一个数的约数加起来又反过来等于这个数。比如284的约数加起来等于220,220的约数加起来等于284,这两个数就是“亲和数”。
有很多关于数论的有趣题目。比如“3X+1”猜想,随便给一个数,如果它是奇数,就乘3加1,如果是偶数就除以2。例如7乘3加1等于22,变成偶数了,再除以2就变成11了,再乘3加1变成34了,再除2等于17,再乘3加1变成52。只要是奇数就乘3加1,只要是偶数就除以2,最后总会变成1,很神奇。
还有“孪生素数”猜想,把数1、2、3、4、5、6……排成一条很长的队,存在无穷多个素数,但后面的素数越来越少。但神奇的是,不管数有多少,总有两个素数会挨在一起,例如3、5挨在一起,11、13挨在一起,17、19挨在一起,29、31挨在一起。这个结果没有人能证明。但是著名数学家张益唐几年前证明:不管往后走多远,总能找到两个素数,它们不是挨到一起,但它们不会离得太远,不会超过7,000万。当然这个结果之后被压缩到100多了。
几何学有更多有趣的问题。如下图:随便画个五角星,五角星上面三角形做外接圆,这些圆两两相交于两个点,有一个点在五角星腰上,另外一个点在外面。江泽民当时拿这个题目去考2002年参加国际数学家大会的数学家们:怎么证明外面这五个点一定是在同一个圆上?
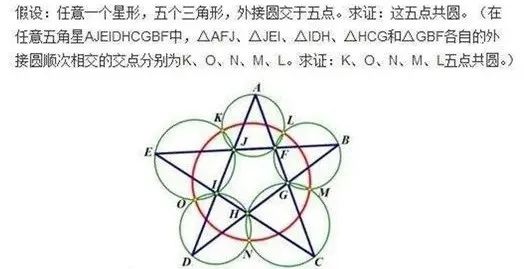
“江五点”问题
数学还有很多形状很有趣,比如每个面都一模一样的是“正多面体”,在三维空间里只有五种可能性:正四面体、正六面体、正八面体、正十二面体、正二十面体。
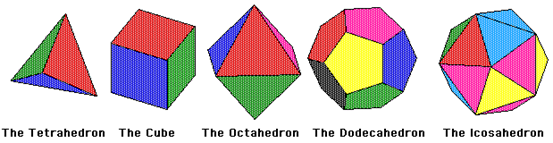
三维空间的正多面体
“莫比乌斯带”也很好玩,蚂蚁在带子上面跑,不翻跟头,就能够把所有的面都跑到,说明它只有一个面。

莫比乌斯带
拓扑学也很好玩。比如有两个人站在地球上,一个往南北方向走,一个往东西方向走,两个人围着地球转一圈,除了这个起点以外,还会交于另一点。但是如果地球形状像轮胎,两个人从拓扑上看就没有别的交点,因为这两个东西结构不相等。美国拍的科幻电影里外星球的组成都是怪怪的,所以我经常说美国拍科幻电影的制作师很懂数学,很懂拓扑学。中国学文科的人,也要懂点数学,也许拍的科幻电影会更有意思。
“拓扑”是两个可以连续变的东西,就像玩橡皮泥,可以捏成各种形状,但都是等价的。几何学家说的三角形有直角三角形、钝角三角形、锐角三角形,但对于拓扑学家来说,这些都是三角形,甚至跟圆都相等。因为它是橡皮泥,可以捏成直角的,也可以不是直角的,但都是等价的,它始终是同一个东西。
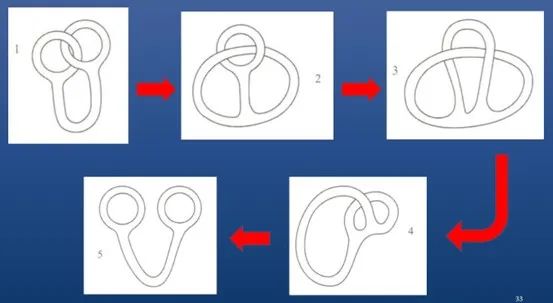
拓扑结构举例
图上像吊环一样的两个东西扣在一起,从拓扑的角度,扣在一起和不扣在一起是一样的。因此,可以利用拓扑性质构造很多好玩的数学游戏。
概率也很有趣,比如扔骰子正面反面的概率是一样的。比如往地板的平行线上面扔针,针落到那条缝上和不落到缝上的概率是跟π有关系的,公式是2l除以dπ。
数学知识可以用来构造游戏,设计游戏。两年前我和撒贝宁老师做了一期《开讲啦》,当时我跟撒老师表演了两个数学魔术,别的魔术师玩魔术都是靠手快、靠道具,而数学家玩魔术就是用数学公式,而且用的都是小学加减乘除简单的公式。
还有微分学的“洛必达法则”,即两个函数的比。如果两个数越来越大,比的是导数,导数就是变化率。就像开车,路程是函数,速度是导数,是变化量。洛必达法则告诉我们:比较两个孩子将来谁的成就大,比的不是现在的起跑线,比的是速度。就像长跑运动员不重视起跑线,而是重视跑步的姿势,跑得是否轻松,速度如何。
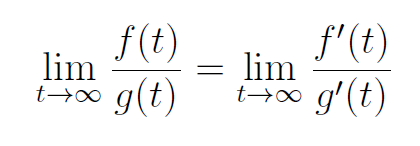
洛必达法则
生活中很多有趣的现象都可以用数学知识来解释或是刻画。比如每个人头顶的头发都有旋,如果没有旋,每根头发都只能竖立起来。用勺子搅拌咖啡,有一点泡泡是不会动的,都可以用数学的“向量场”来刻画和解释。
向量场
数学的第四个特点是“难”。我做了一些调研,果真很多人认为数学很难,包括学生家长、大学生、研究生,甚至做研究的人都觉得数学很难。数学为什么难?首先是难在数学有独特的语言,独特的描述方式。著名科学家哥白尼说:数学就是为数学家写的。如果不是数学家,对数学语言就不熟悉。德国著名文学家歌德把数学家比喻成“法国人”,并非褒义词。
第二个原因是数学的证明非常复杂。著名数学家波利亚说:数学就是把最明显的事情用很不明显的方式证明。而且数学的证明高度抽象,大众很难理解。比如费马大定理,把勾股定理的平方换成n,Xn加Yn等于Zn没有正整数解。安德鲁·怀尔斯证明费马大定理的文章从443页到551页,证明了100多页,还只是临门一脚。费马大定理完整的证明基于很多定理,最后临门一脚都写了100多页,可见很深奥。
数学是个“大骗子”。因为大家学什么都叫学数学,比如小学1加1等于2是数学;初中解方程、三角函数、几何也是数学;大学微积分也是数学,很容易让人迷惑。就像三轮车骑得好,不等于山地自行车骑得好,山地自行车骑得好,不等于杂技玩得好。文科就没有这个问题,沈从文散文写得很好,莫言长篇小说写得好,苏东坡词写得好。
而且,并不是小学数学100分,中学数学就一定学得很好,因为不同阶段的数学内容完全不一样,容易大意,掉以轻心。
数学的第五个特点是“慧”。做数学需要聪明和智慧。比如古希腊著名数学家埃拉托色尼,号称“世界地理之父”。毛主席说过“坐地日行八万里”,即绕地球一圈是四万公里。埃拉托色尼在公元前200多年就精确地算出地球一圈是四万公里,这并不是一件容易和简单的事。伟大的数学家埃拉托色尼外号是“β”,英文字母α、β,β排在第二,相当于中国人说甲、乙,乙就是乙等生,所以他外号的意思是“千年老二”,因为同时代的数学家们太厉害了,例如欧几里得、阿基米德,所以即使埃拉托色尼那么伟大,他也是“千年老二”的数学家。
但无论如何,数学家都很聪明,菲尔兹奖奖牌的正面是阿基米德的头像,有一行拉丁文写道:“超越人类的极限,做宇宙的主人”,的确是口气很大。
牛顿是非常著名的数学家,也是有史以来最伟大的数学家。关于牛顿有一个非常著名的传说:牛顿老年功成名就之后,有人问他为什么取得那么大的成就?牛顿的回答是“因为我站在巨人的肩膀上”。但这个故事有另外一个版本:牛顿说“我能取得那么大的成就,是因为我在不断地思考”。我更愿意相信后者,各行各业,不管什么领域,一定要不断思考,才能在自己的领域有所创造和建术。
其实数学是对“想象力”要求非常高的学科。爱因斯坦曾说:想象力比知识更重要。著名的数学家摩根说:数学发明不是推理,更重要的是想象力。可见数学对想象力的要求非常高,而且数学的很多重要发现都是凭直觉的“无中生有”。
有的数学家的确非常有天赋,数学的确是智者的游戏。但天赋固然重要,更重要还是“努力”。华罗庚是中国近代最伟大的数学家,他说:聪明在于勤奋,天才在于积累。华先生的最高学历是初中,自学成才,靠的就是努力。
数学的作用
关于数学的作用,首届数学节的主题是“数学无处不在”,这是数学圈子认可的,但是很遗憾,社会对数学的作用并不太认可。
给大家讲一个笑话:有甲乙两人坐热气球去探险,漂到海上迷路了。漂了三天三夜,总算漂到一个陆地上,陆地上有一个人是丙。甲跟乙就像看到了救命稻草似的问丙“我们在什么地方”,丙看了一眼热气球上的两个人,很冷静地回答说“你们两个人在热气球上”。甲无语地对乙说“下面那个家伙一定是个数学家”,乙问甲何以见得,甲回答“我们问了他一个问题,他给了我们一个回答,这个回答完全正确,但是毫无用处,这不就是数学家干的事吗?”
再讲一个笑话:大概在100万年以前,恐龙把地球上的树叶都吃光了,食物链断了,恐龙开始吃人。有一个部落的一个人武功非常高,他把周边的恐龙都杀光了。消息一传十、十传百,全地球都知道了,都派人来学习杀恐龙。这个人就开了一个杀恐龙学校,教了很多学生。这些人都学会了杀恐龙,就回到当地继续教当地人杀恐龙,又办了很多学校,会杀恐龙的人越来越多,最后恐龙都被杀光,灭绝了。过了几百万年,突然有个小朋友问老师,恐龙都已经灭绝几百万年了,我们还学杀恐龙技术有什么用?老师说可有用了,你将来毕业后可以去当老师,教别人杀恐龙,数学家不就这么做的吗?
这两个笑话是公众在讽刺数学“无用”,但事实并非如此。其实中国古代的数学从诞生开始就是有应用的,《九章算术》讲量地、农贸市场买东西、鸡兔同笼等等,这些数学题目都是来源于真实生活的。很多科学家对数学的作用都有较高评价,著名科学家达尔文说:数学为其他学科的新发现提供指导和表达形式。达·芬奇说:数学是所有自然科学的基础,不用数学的学科一定还未成熟。著名数学家切比雪夫说:数学不能跟实际相脱离。印度著名的社会活动家戴维说:没有数学,基本上什么都不能做。笛卡尔认为:数学是最有效的一个工具。
数学在中国的疫情分析方面也起到很大作用。医院体检的CT机,不仅仅只是个设备,它背后的原理是数学。没有数学,没有“拉东变换”,不可能造出CT机。
数学无处不在。比如工程建筑盖房子,如果没有用“有限元计算”,施工单位是不敢盖房子的;修桥梁、修水坝、建高楼大厦,都是通过数学方法计算才安全施工;地球勘探、天气预报等,都在使用数学知识。为什么天气预报越来越准了?是数学方法的进步。包括航空航天,背后都跟数学有关系。目前大数据、人工智能非常火,数据很重要,算法都是基于数学。在图像处理方面,曾当过国际数学联盟理事长、主席的女数学家多贝西为“小波变换”做出了巨大贡献。如果没有数学,照相机甚至无法存储高清照片。菲尔兹奖获得者陶哲轩所做的压缩感知相关奠基性的工作,也是做出了巨大贡献。
在通信方面,中国5G最终没有被美国卡住脖子,因为中国的通信技术在国际上遥遥领先,任正非老先生呼吁重视数学,因为一个数学理论,能够导致整个产业的变革性进步。
在电网方面,我们用的电、电网的调配、控制都跟数学有关系。
金融经济方面更不用说。诺贝尔奖设有物理学奖、化学奖,却没有设数学奖。但很多数学家得了诺贝尔经济学奖,一位是纳什,还有一位是詹姆斯·莫里斯,他是北大光华管理学院张维迎的老师。所以很多获得诺贝尔经济学奖的都是数学家,说明数学在经济方面用处非常大。
此外,数学追求自身的逻辑体系,我们对待数学不要太苛刻,尤其要给做数学基础研究的人轻松平和的环境。周向宇院士反复强调做基础科学无用之用,他做真正的纯基础研究,我们很敬佩这种完全是为了探索,追求人类智慧极限的纯数学家。
数学与伟人
最后想谈谈伟人和数学的关系,他们很重视数学。马克思在给恩格斯写信时说:“有空时我研究微积分”,他留下了100多页数学手稿,可见马克思酷爱数学,对数学颇有研究,而且他教女儿珍尼要整理他跟恩格斯的书信和数学手稿。
另一位伟人是美国开国元勋华盛顿,他说:“对数学的探索,让头脑习惯于推理和求真”。所以学数学不是为了做题,为了考试,为了高考,为了家长,学数学最重要的目的是养成严格逻辑推理的品质和好习惯,是追求真理和事实对错。学数学会影响为人,学会在这个世界上做任何事情都要讲道理。将来你的孩子不一定要当数学家,但当领导干部或者企业家,也需要科学地做决策,而不是拍脑袋。
另一位著名伟人是欧洲著名政治家、法兰西皇帝拿破仑,其实他是数学院院士,他在签署法兰西法令时,把他是法兰西科学院院士,看得比法兰西皇帝还重。
毛主席对数学也是很关注的,他跟华罗庚都有书信来往,足见我们国家领导人对数学的关注。
中国数学的发展
中国近些年数学发展得很好。首先是中国的年轻学子近年在国际奥林匹克数学竞赛取得了非常好的成绩。二是中国做研究的数学家在国际上的影响力越来越大。国际数学家大会每四年召开一次,中国数学家历史上参加的人屈指可数,仅华罗庚、冯康、吴文俊等大腕院士可以去做报告。但近年,每次开会华人数学家都有十几人参加,影响力越来越大。2023年在东京召开的国际工业与应用数学大会,中国有1000多人参会,北大著名数学家鄂维南院士做了大会报告“AI For Science”,可见中国数学家在国际上的影响力越来越大。
李克强去北大时接见姜伯驹、田刚等科学家、院士,对基础研究非常重视。中国科技部、教育部、中科院近年对数学都非常重视,特别是科技部设立了“十四五”数学专项,也成立了很多数学研究中心。
最后,我希望不管你是否喜欢数学,千万不要以不懂数学为荣。不管自己数学好不好,还是要培养孩子学好数学。新闻记者、媒体在舆论上要鼓励更多的人尤其是青少年朋友喜欢数学,热爱数学。学数学不是重复刷题,而是在理解的基础上培养兴趣。
数学无处不在,非常有用。学好数学总是没坏处,优点多多益善,用数学语言,即如果B>0,必有A+B>A。希望大家都要重视数学、学好数学。
感谢陈杲教授提供专业建议。
袁亚湘,1981年毕业于湘潭大学,1986年获英国剑桥大学博士学位。中国科学院数学与系统科学研究院研究员。中国科学院院士、发展中国家科学院院士、巴西科学院通讯院士、美国数学会首届会士、美国工业与应用数学学会会士、伦敦数学会荣誉会员。现任中国科协副主席。主要研究非线性最优化计算方法,在信赖域法、拟牛顿法、非线性共轭梯度法、子空间方法等方面做出了重要贡献。曾任中国数学会理事长、中国运筹学会理事长、国际工业与应用数学联合会主席、国际运筹学联合会副主席。曾获国家自然科学二等奖、发展中国家科学院数学奖、何梁何利科技进步奖、美国工业与应用数学学会杰出贡献奖等。还曾获“中国十大杰出青年”等荣誉称号。
本文转载自:墨子沙龙,内容来自墨子沙龙活动“数学漫谈”(2024年4月21日)上的演讲。演讲嘉宾是中国科学院数学与系统科学研究院研究员袁亚湘院士。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 