2023年日本京都奖授予美国数学物理学家Elliott H. Lieb， Lieb基于其多体物理学方面的工作，为物理学、化学和量子信息科学等领域的数学研究奠定了基础；也对数学分析做出重要贡献。京都奖官方称他是数学科学领域的智力巨人之一。在获奖后的公众讲座中，他讲述了自己半个多世纪以来的物理学和数学研究历程（文中照片为Lieb讲座中使用的）。

原视频地址：https://www.youtube.com/watch?v=kwn8ySt0vH8&list=PLmPcz49VTBBerReYZr-IE9kPl7SFvB3_F&index=7&ab_channel=KyotoPrize

演讲 | Elliott H. Lieb

整理 | 叶凌远

我于1932年在美国波士顿出生，但我是在纽约市长大的，也在那里形成了我的世界观。我们家属于中产家庭，但纽约市提供了非常优质的免费公立教育。我发现我喜欢创造，喜欢参与业余无线电活动。我最自豪的是莫尔斯电码学得很不错，取得了无线电W2ZHS执照，可以连接全球所有其他的操作员，与他们传递信息。这些爱好与努力受我表哥的影响很大，我曾以为这会引领我走上电气工程师的道路。17 岁时，我随全家一起搬回了波士顿。我极其有幸受到了著名物理学家 Victor Weisskopf 的推荐与鼓励，进入了麻省理工学院，即人们所称的 MIT。

Lieb度过大学时光的MIT（1949-1953）丨图源：Wikimedia

在1949 年我进入麻省理工学院后不久，第一门物理课就改变了我的想法。Matthew Sands 是广受欢迎的《费曼物理学讲义》的合著者之一，他让我领略到了牛顿物理学在智识上的美。起初，我很难掌握这些内容，高中的课程并没有真正让我有能力深入理解物理学定律，例如牛顿方程到底意味着什么。我花了一段时间才弄明白牛顿方程。它的含义正如其表示的：力等于质量乘以加速度。要知道物体的加速度，必须先知道力和质量的大小。在不同的场景下，这些物理量的具体数值会有所不同，但背后的原理是一致的。在 Matthew Sands 耐心的帮助下，我花了一半的课程时间理解了这个方程的重要性，我的科学生涯自此有了一个良好的开端。与牛顿同时代的人一定也遇到过与我类似的困难。自那以后，我放弃了成为工程师的想法，在后续本科学习过程中转向了纯物理课程。作为 MIT 的本科生，我非常有幸在研发早期粒子直线加速器的实验室找到了一份兼职。现在实际运行的加速器都非常大了，但那时其体积还很小。这台1700万电子伏特的机器的建造者，Isaac Halpern 和 Peter Demos，是我遇到过的最鼓舞人心的人。他们对我的本科生涯产生了很大的影响。

Bates直线加速器丨图源：MIT Museum

对1949年的民众而言，物理并没有像化学那样为人所熟知。我的父亲曾认为，我突然决定投身物理会让我将来陷入贫困。但事实并非如此。我很幸运赶上了二战后政府资助自然科学的浪潮，过上了体面的生活。数学在我的学习中占据了一定的份额，但并不是很多。我最有幸的是，在 MIT 向 Isadore Singer 学习了高等线性代数，后者因 Atiyah-Singer 指标定理而闻名。我与他随后成为了很好的朋友。

在 MIT 毕业后，我想去看看更大的世界。到那时为止，除了几个较大的美国城市，我没有去过别的地方了。在 Weisskopf 教授的指导下，我毕业论文写了与相对论有关的题目。他认为，英国伯明翰大学数学物理系有 Rudolf Peierls 教授和 Sam Edwards 与 Gerry Brown 两位讲师，是整个欧洲做理论物理最好的地方之一。并且，他们都说英语。这对我很重要，因为我那时还没有接触过任何一门外语。John Bell 是我那时的同学，他后来发现了一个对量子信息而言极其重要的不等式。

英国伯明翰大学（1953-1956）丨图源：University of Birmingham

那些年我的确实现了愿望，游历了欧洲大多数的国家。在伯明翰度过了三年，我写了一篇乏善可陈的博士论文，于 1956 年获得了博士学位。下一站我就到了京都，因此我获得博士学位后的第一份工作是在日本。为什么选择京都？我的叔叔在波士顿开了一家艺术书店，专营日本艺术，他让我对浮世绘产生了浓厚的兴趣。在伯明翰，我有幸和一位名叫吉田四郎（Shiro Yoshida）的日本核物理学家共用一间办公室。我被指派帮助他提高英语水平，我做到了，而他则教我一些基本的日语作为回报。他没有教我日语汉字，只是听说，所以还是像文盲一样。

Lieb博士毕业后来到京都（1956-1957）丨图源：Japan Guide

尽管如此，美国富布赖特项目（Fullbright Program）为我提供了一年的资金，让我得以前往京都大学基础物理学研究所（YITP），这里也被称为汤川纪念馆（Yukawa Hall）。无论从文化方面还是科学上，那一年的经历都对我产生了深远影响。在那之前，我一直怀疑我能否对科学做出有价值的贡献。在京都，我认为我做到了。离开京都后，又过了四年我才再一次做到这一点。

京都大学基础物理研究所丨图源：Katsura Roen/Wikimedia Commons

在京都大学基础物理研究所，我遇到了山崎和夫（Yamazaki Kazuo），一位才华横溢的年轻日本物理学家。我与他保持了密切的合作关系，我们一起研究物理中很具有挑战性的极化子模型（Polaron model），它描述了被限制在晶体内电子的运动。这在那时是一个热门的方向。我们决定要超越从物理直觉出发的计算，在数学上严格计算出极化子模型的基态。我们证明极化子的能量实际上是有限的，换言之，基态是存在的。其他物理学家，如费曼，则认为这是不言自明的，尽管其他与此类似的物理模型中基态都不存在。就这样，极化子的相关研究和我们两人的生活都迈入了新的篇章。

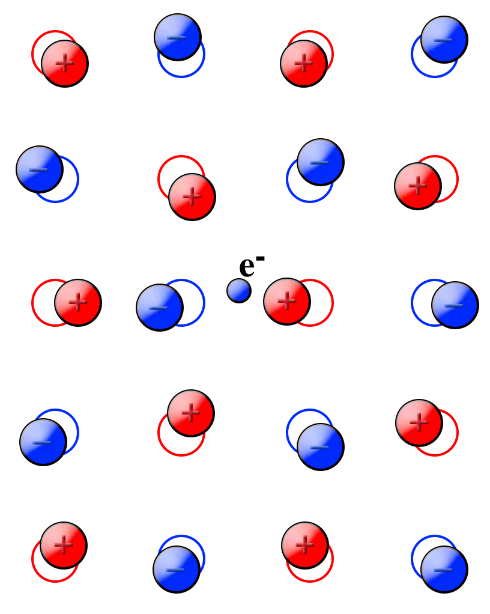
极化子（Polaron）丨图源：Wikimedia

正是这一段在京都的经历，让我确信我有能力做科研。两年后，我在康奈尔大学见到了费曼本人，他询问我的兴趣是什么。我自豪地向他介绍我在京都与山崎和夫一起做的工作，他相当激进地回复说：“真正的物理学家不做那样的研究！”在他眼里，我作为一个年轻的学者浪费了自己的时间。这一负面的评价让我更坚定不移地选择了数学物理这条道路，并坚信它对物理学的意义。

伊利诺伊大学（1957-1958；左）和康奈尔大学（1958-1960）丨图源：Wikimedia

从京都离开后，我在伊利诺伊大学待了一年，随后又在康奈尔大学待了两年，在著名的诺贝尔物理学奖得主Hans Bethe 手下工作，正是他解释了太阳发光背后的核反应机制。然而，这三年我一无所获，这让我对自己作为一名数学物理学家的未来感到担忧。但这一时期也让我遇到了伴随我一生的问题，即对玻色气体的研究，特别是其最低能量态。玻色气体是以印度物理学家Satyendra Nath Bose的名字命名的，具有特殊的量子性质。因此，我在最顶尖的大学、最顶尖的物理学家手下工作了两年，直到1960年离开，我获得的仅仅是一个值得思考的问题。这个问题在我脑海中萦绕了三十六年。直到许多年后，我才与 Jakob Yngvason 于1996年解决了这一问题，这也引发了现在数学物理领域对玻色气体的兴趣。

在康奈尔之后，我去了位于纽约约克敦高地的 IBM 计算机研究中心。那是 1960 年，该研究中心在这一年刚刚成立。这是我拿到的第一个永久性职位，尽管我只在那里待了三年。我很幸运与两位和我年龄相仿的同事共事，Ted Schulze 和 Dan Mattis。那时，我们三位学物理的人希望从数学的角度证明某些已经被接受的理论。这种兴趣超出了其他所有工业界实验室研究的范畴，因此我们很感激 IBM 给了我们这样做的自由。

总体来说，1960 年到 1970年是世界物理学研究辉煌的十年，物理学中几个重要的定理都出自这一时期。其中一个是 Lieb-Schultz-Mattis 定理，即一维的物质永远不会被磁化。也就是说，一根原子链永远不会产生磁性，至少需要有两个维度才行。当时大多数的理论物理学家，包括著名的德国物理学家海森堡、我在伯明翰的博士生导师 Peirels 教授，以及我在康奈尔的导师Bethe，所设想的与此完全相反，他们曾认为在一维物体中磁化必定会发生。而我们证明了这永远不会发生。我们花了一些功夫说服这些同事我们的结论是正确的，Peirels 最终接受了我们的数学证明。这是量子力学中最早引起广泛关注的数学证明之一，我们后来就此继续发展了几个定理。

《一维数学物理学》（Mathematical Physics in One Dimension，1966）的重印本。丨图源：E. Lieb

在 IBM 的第二年，我去了塞拉利昂（译者注：利用休假），这是西非的一个国家，我在该国首都弗里敦的一所大学教授了一年应用数学。当时这里发生了很多社会政治运动，还暴发了疟疾。顺便一提，如果你没有得过疟疾，我可以告诉你这是一种令人非常难受的疾病。

Lieb利用学术休假在塞拉利昂Fourah Bay College任教一年 丨图源：Wikimedia

也因如此我在那里有时间思考科学问题。正是那时我发明了一维玻色子的模型，后来回到 IBM 后，我与 Werner Liniger 一起求解了这一模型。现在，这一模型对理解量子力学多体问题起到基础性的作用。虽然该工作是有关一维原子链的模型，但后来也被实验证实了。在纽约叶史瓦大学工作了两年后，我又回到了波士顿，在东北大学担任教授。在那里，我与伍法岳教授合著了《物理评论快报》（PRL）史上被引数最多的论文，求解了一维的赫巴德模型（Hubbard Model）。它至今仍保持着该期刊文章中被引用次数的最高纪录。

PRL上被引用次数最多的论文在东北大学期间，我把兴趣转向了其他领域：冰。水降温后会结成冰，但冰并不简单。冰和数学有什么关系？Linus Pauling 有一个非常重要的观察，他说冰的熵可以通过思考水分子的排列方式来计算。我们知道，水分子由两个氢原子和一个氧原子组成。实验发现，在绝对零度下，冰的熵也不会降为零。这是物理学史上最精妙的实验之一。换句话说，冰中有一部分内蕴的熵，怎么也不会消失。这意味着冰中氢原子和氧原子的排列，即水分子的朝向，有着显著的随机性。

一种描述冰的方法是将其想象为由箭头组成的晶格模型。在这个模型中，每个点代表氧原子，箭头代表氢的位置，它总是位于两个氧原子之间，可以指向一侧或另一侧。正如我所说，即使在绝对零度下，冰中仍有一些变化存在，需要计算其重新排列的总数。这正是我所着手去做的。顺便一提，这个模型是由 Linus Pauling 发明的。如下图所示，在氧原子位于晶格上规则排列的情况下，冰的熵就等于氢原子排列方式总数的对数。同时，要形成冰要求每个顶点都有两个箭头指向它，两个箭头背离它。

二维冰模型丨图源：Vadim Gorin

因此，计算冰的熵等价于计算在这张图中符合规则的箭头排列方式的总数。经过计算，该排列方式总数为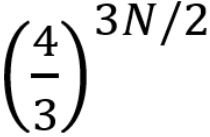。而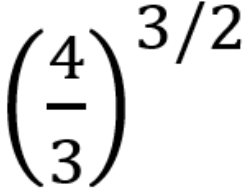约等于 1.54，该常数现在也以我的名字命名。这一结果催生了组合数学中的一个新分支，称为“六顶点问题”。因为在每个顶点处，如果有两个箭头指向它，两个箭头背离它，那么一共有六种可能的排列方式，你必须计算出在每个顶点处都同时符合这种配置的总排列方式。这延伸出了组合数学一个完整的子领域。我的贡献在于找出了满足要求的排列方式的总数，当然这一领域还有许多开放的问题，至今没有得到解决。接下来的几年是我与 Joel Lebowitz 合作的高光时期。我们证明了库仑力的热力学极限存在。这一定理，和 Freeman Dyson 与 Andrew Lenard 证明带电粒子具有能量下限的结论一起，证明了“物质的稳定性”。让我来稍微解释一下这一概念。一个原子，如你在这下图中看到的那样，有一个原子核，以及围绕原子核旋转的电子。电子所带电荷量与原子核所带电荷量相等。而要构成宏观的物质，需要很多原子组合在一起。

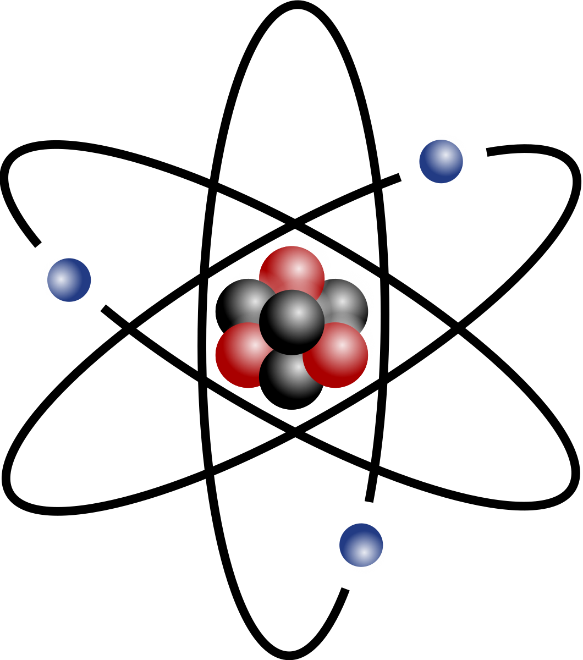
物质的稳定性（The Stability of Matter）丨图源：Indolences/Wikimedia Commons

问题是，为什么这些原子核和电子排列构成的物质——看起来就像蜘蛛编织的产物——不会不稳定？宏观物质本质上由无穷多核子和电子组成，但似乎没有任何东西把它们紧紧地结合在一起，为什么它会如此稳定？你可以敲击它，它不会散开，尽管它是由上述图片中所示的那些东西构成的。在物理学中，人们慢慢才意识到这个问题，而我们决定去解决它。上述图像虽然粗糙，但没有原则性的错误。原子之间的确可以相互吸引，但吸引力非常微弱，并且它们仍保持各自的完整性。在数学上解开这个谜团花费了几十年的时间，我也为解决这个问题做出了一些贡献。这个问题的解决得益于多位学者共同的努力。如上述提到的 Dyson 和 Lenard，以及我的同事，还有 Walter Thirring。随后在1973年，Mary-Beth Ruskai 和我一同证明了量子熵的强次可加性（Strong subadditivity of quantum entropy）。从数学的角度来看，这一结论是量子计算的基石之一。证明该结论需要大量的数学分析，这也开启了我从事纯粹泛函分析的阶段。这个时期我其他的工作包括证明了另一组解析不等式，即现在人们所称的 Brascamp-Lieb 不等式，这些不等式在量子信息理论中有非常广泛的应用。Herm Jan Brascamp 是一位年轻的荷兰数学和物理学家，我们那时在一起工作。时间来到1975年，我接受了来自普林斯顿大学的职位，加入了它的数学系和物理系。在同一年，我与维也纳大学的 Walter Thirring，全球最知名的数学物理学家之一，建立了友谊。之前提到过的 Dyson-Lenard 对物质稳定性的证明事实上较为复杂，而我们认为应该有更为简洁的证明，不需要那么多页的计算，并能得出更好的稳定性估计。我们最终取得了很大的成功，且发明了一类全新的数学不等式（Lieb–Thirring inequality），现在它们以我俩的名字命名。让我再提及一些后来发生的事情。其中一个较为有益的成果是所谓的 Lieb-Oxford 界限。与Steve Oxford 合作时，我们找到了一个此前甚至没有人设想其存在的界限，该界限与固体中的能量交换有关。我不会进行更详细地解释了，大家将其理解为使固体保持稳定的能量即可。是否有关于这个能量极限的任何估计？它可能会有多大？我们得到了这样一个估计，而这是出乎人们意料的。在1979年，我很幸运在学术休假时和我的妻子 Christiane Fellbaum 一起再次来到京都，她正坐在台下。我们经历了许多激动人心的事情，但也许其中最重要的一件事是关于电车的。我们在今出川通，见证了京都电车最后一次停下的瞬间。这是一个很有纪念意义的事件，现场有很多人。我清楚地记得这辆电车沿着轨道滑行，突然停下来，最后的电车就这样终结在我们面前。

Lieb回到京都（1978-1979），见到了日本第一条有轨电车的停运丨图源：Brendan Barrett

至于我之前提到的有关固体能量交换极限的工作，实际上就发源于我在京都的时期。但之后在普林斯顿，我和 Oxford 一起将这一界限改进到了现在的数值。

另一篇同样具有影响力的论文也和日本有一定关系——有关电子自旋的 AKLT 模型。其中，A 代表Ian Affleck，K 代表Tom Kennedy；T 代表田崎晴明（Hal Tasaki），他是我1987年的博士后，今天也在现场。这是凝聚态物理中最早展示最低能量态和下一个能态之间存在能隙的模型之一。很少有物质具有这种性质。通常情况下，物质状态的能量是从底部向上连续变化的，而在这里却存在一个能隙，这个能隙如今在大家习惯使用的电子产品中起到了很重要的作用。我想提的最后一件事，就是我与Jakob Yngvason合作的对热力学熵意义的研究。熵是热力学中最古老的概念之一，可以追溯到十九世纪初热力学的开端。然而，熵到底是什么？它除了是一个可以（间接）测量的物理量之外，是否还有其他意义？独立于玻尔兹曼所设想的原子和分子跳跃碰撞的图景，熵还有没有什么其他的意义？难道熵就是粒子的运动？答案是否定的。熵具有更普遍的意义，它如今也在许多不同的领域中出现，比如计算机科学。我们找到了熵的意义，它作为一个指标，表明了哪些状态转变是可能的。这就是熵。我们以一种完全独立于任何物理模型的方式，解释了熵的真正含义。熵指示了什么是可能的，什么是不可能的，而判断标准则取决于起始状态的熵是否小于最终状态的熵。熵是一种计数方法，其表明的普遍规律则是，尽管物质原则上可以从一个状态转变到另一个状态，但在大多数情况下，这种转变只能朝一个方向进行，而这个方向是由一个叫作熵的简单函数决定的。这提供了一种理解熵的全新视角。在这次演讲中，我提及了多个我有幸参与的数学、物理以及数学物理领域的研究。我十分荣幸与来自多个国家——特别是日本京都——的许多杰出同事进行合作，并在这一过程中得到了足够的支持和鼓励。尽管在职业最初有过疑虑，但我坚持了下来。我怀着谦卑的心情感谢稻盛财团授予我京都奖，并给予了我这个机会，让我能够分享我的生活和工作。谢谢大家。

本文基于知识共享许可协议（CC BY-NC）译自Elliott H. Lieb “My Journey Through Physics and Mathematics”