撰文 | 丁玖（美国南密西西比大学数学系教授）

伟大的人物通常也是幽默家。氢弹之父乌拉姆（Stanislaw Ulam，1909-1984）曾有一句诙谐之语：“把混沌研究称为‘非线性分析’，就好比把动物学说成是‘非大象一类动物的研究’。”

事实上，虽然确定性意义下的“混沌”定义迟至上世纪70年代中期才问世，然而，对它“遍历性”的探索比之更早四十五年就开始了：以30年代初的冯·诺伊曼平均遍历定理和伯克霍夫逐点遍历定理这两个经典遍历定理为主要代表，而现代遍历理论的研究可以说是以乌拉姆为领头羊的。 

探索“混沌”的“不变密度函数”法

从我之前的《从统计的角度看混沌》文中可知，要想发现混沌映射S迭代点轨道的统计分布，就必须找到对应的弗罗贝尼乌斯-佩隆算子P_S的密度函数不动点，即求出不动点方程P_S f = f的密度函数解，称为不变密度函数。它定义了一个绝对连续的概率测度，称为该映射的不变测度，其“不变性”意指任一子区间的测度值等于它在S下的逆像的测度值。只要映射关于该不变测度是遍历的，根据伯克霍夫逐点遍历定理，我们就能通过这个不变测度来描绘出混沌轨道的统计性质。称概率测度μ是绝对连续的，意思是指μ可由积分表示，即存在一个密度函数f，使得所有子区间I的测度值μ(I) 等于积分 ∫_I f(x) dx。与绝对连续的测度相对立的是奇异的测度，如著名的狄拉克测度。

伯克霍夫逐点遍历定理可简述为：若具有不变测度μ的映射S是遍历的，则对μ而言几乎所有的初始点x₀，时间平均 = 空间平均，即。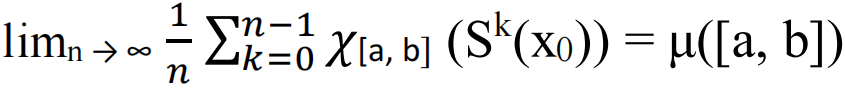

“遍历”一词在数学上是何意思呢？我先用一例来说明“不遍历”的含义，帮助想象“遍历”意味着什么。定义一个将[0, 1]映到自身的映射S：当0 ≤ x < 1/4时，S(x) = 2x；当1/4 ≤ x < 3/4时，S(x) = 2x – 1/2；当3/4 ≤ x ≤ 1时，S(x) = 2x – 1。下面是S的图象：

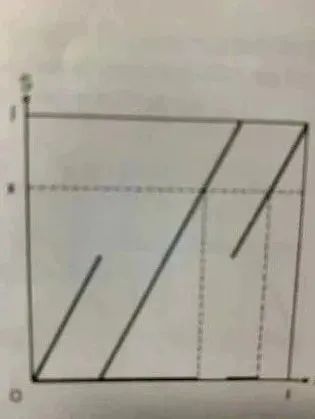
易知在S下，区间[0, 1/2]的逆像是[0, 1/2]，区间[1/2, 1]的逆像是[1/2, 1]，即S^-1([0, 1/2]) = [0, 1/2])和S^-1([1/2, 1]) = [1/2, 1])。这表示[0, 1]的子区间[0, 1/2]和[1/2, 1]是S的不变集。由于这两个不变集的存在，原先的映射S实际上可以分解成两个互不相干的映射S₁: [0, 1/2] → [0, 1/2]和S₂: [1/2, 1] → [1/2, 1]，它们分别是S在子区间[0, 1/2]和[1/2, 1]上的限制，其各自的图象分别是上面S图象的左下半个和右上半个。尽管长度（实变函数论中勒贝格测度的通俗说法）是S的不变测度，但是伯克霍夫逐点遍历定理此时并不成立，例如当初始点x₀属于[0, 1/2]时，由于所有迭代点都在[0, 1/2]内，[0, 1/2]的时间平均为1；若x₀属于(1/2, 1]，由于所有迭代点都不在[0, 1/2]内，它的时间平均为0。而[0, 1/2]的空间平均却为区间长度1/2，因此对于这个例子，时间平均并不等于空间平均。

从上面这个非遍历的映射例子可以想出“遍历映射”的定义。对于任意一个将定义域映到自身的映射，总有两个平凡的“不变集”，它们是空集和定义域本身，因为它们在该映射下的逆像就等于自己。如果映射本质上不存在“非平凡”的不变集，即不存在定义域的一个非平凡子集，使得它与其在映射下的逆像是同一个集合，则它是遍历的。简言之，如果映射仅有平凡不变集，它就是遍历的。

何时存在“不变密度函数”？

一个自然的问题就出现了：给定映射S: [0, 1] → [0, 1]，它所对应的弗罗贝尼乌斯-佩隆算子P_S有不变密度函数吗？先回忆该算子的定义：对每一个[0, 1]上的可积函数f，

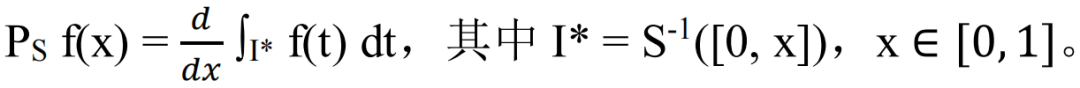
我在《从统计的角度看混沌》中用简单易懂的例子引进了这个算子。

考虑“减半映射” S(x) = x/2，它的定义域是[0, 1]，值域是[0, 1/2]。易知当0 ≤ x ≤ 1/2时，S^-1([0, x]) = [0, 2x]；当1/2 < x ≤ 1时，S^-1([0, x]) = [0, 1]。因此P_Sf的表达式为：当0 ≤ x ≤ 1/2时，P_Sf(x) = 2f(2x)；当1/2 < x ≤ 1时，P_Sf(x) = 0。由此显见，不动点函数方程P_Sf(x) ≡ f(x)只有零解f(x) ≡ 0。这并不奇怪，因为所有迭代点数列{Sⁿ(x₀)}都收敛到S的唯一不动点0，故无绝对连续的不变测度。顺便说一下，对减半映射，非绝对连续的在0点处的狄拉克测度是其不变测度。

上面的例子比较简单，容易理解，下面是一个非线性映射的例子，它也同样没有绝对连续的不变测度，即它所对应的弗罗贝尼乌斯-佩隆算子没有非零不动点。这个映射定义如下：当0 ≤ x ≤ 1/2时，S(x) = x/(1 - x)；当1/2 < x ≤ 1时，S(x) = 2x – 1。这时，懂得初等微积分并精通高中代数的读者容易算出P_Sf的表达式为

P_Sf(x) = (1+x)^-2f(x/(1+x)) + (1/2)f(1/2+x/2)。

在洛速达（Andrzej Lasota，1932-2006）与麦基（Michael Mackey，1942-）合著的书Chaos, Fractals, and Noise：Stochastic Aspects of Dynamics（《混沌、分形与噪音：动力学的随机方面》）第六章第二节内，作者给出了上述算子只有零函数这个唯一不动点的证明。

注意到前面两个例子的不同之处：第一个映射的导数恒等于1/2，它严格小于1；但第二个映射的导数在(0, 1]上处处严格大于1，但在x = 0处等于1。这向我们提出一个问题：如果一个映射在定义域区间上导数除了几个例外点外处处存在，并且导数的绝对值都严格大于1，其对应的弗罗贝尼乌斯-佩隆算子一定有非零不动点吗？满足上述导数条件的映射被称为是“逐段拉长的”，这个性质是混沌的一个发源地，但不是必要条件，因为混沌的逻辑斯蒂映射S₄(x) = 4x(1-x)并非是逐段拉长的。纵观混沌观念发展史，乌拉姆无疑属于最早几个对此性质进行过探索的数学家之一。

学过初等微积分的读者应该知晓，逐段拉长的映射不可能在整个定义域区间上处处可微，否则根据被称为“微分学基本定理”的拉格朗日中值定理，该映射的值域区间将比定义域区间更长，这与值域包含于定义域的基本假设相矛盾。我们熟悉的逐段拉长的帐篷映射T在x = 1/2这一点导数不存在这一事实也表明了这点。因此，逐段拉长的区间映射只能通过“分段可微”而实现“逐段拉长”。

乌拉姆传奇

乌拉姆是“非线性分析”这门综合性研究领域的先驱，实际上他与终生朋友冯·诺伊曼（John von Neumann，1903-1957）及物理学家费米（Enrico Fermi，1901-1954）等几位智者在从事原子弹研制中创建了这门学科。多年前，我读过乌拉姆文集Science, Computers, and People（《科学、计算机及故友》）。数学科普家伽德纳（Martin Gardner, 1914-2010）撰写的前言第一段是：“乌拉姆， 或如同他朋友所称之的斯坦，是那些伟大的创造型数学家之一，这些人不仅对数学的所有领域感兴趣，而且同样对物理及生物科学亦然。和他好朋友冯·诺伊曼一样而与他众多的同行不一样的是，乌拉姆不可被分类为纯粹或应用数学家。在那些与应用问题没有一丝一毫关联的纯粹地带，以及在数学的应用中，他都从不停止寻找同样多的美和激动。”

乌拉姆是犹太人，他的出生地利沃夫原属奥匈帝国下的波兰，现属乌克兰，位于国土的西部，所以他是波兰/乌克兰裔数学家，在“万神殿”网页（pantheon.world）上被列为有史以来最传奇的十位乌克兰数学家之首。在他那本我已读过三遍的脍炙人口的自传Adventures of a Mathematician（《一位数学家的经历》）一开头，乌拉姆就告诉读者，他四岁时就对家中客厅铺的波斯地毯上的几何图案着迷。当他身为律师的父亲对此不以为然而笑起来时，他心里自言自语道：“他笑是因为他认为我是幼稚的，但是我知道这些是令人好奇的模式。我知道我父亲所不知道的某样事情。” 这或许就是他终生热爱探讨新事物的天赋之才的最初显示。他喜欢提出问题以及解决问题的另一个佐证是，在上世纪30年代波兰数学学派名扬天下之时，以泛函分析集大成者巴拿赫（Stefan Banach，1892-1945）为首的波兰数学精英在苏格兰咖啡馆讨论数学及时记下的数学问题录——现在国际数学界名闻遐迩的《苏格兰书》——以二十多岁时的乌拉姆贡献的问题最多！

正是由于喜欢与人讨论，喜欢提出问题，乌拉姆从他大脑里萌芽而出的“对要点的感觉”，日后成了几个数学领域的开始之旅。比如，“细胞自动机理论”最初是他向冯·诺伊曼提出来的；“蒙特卡罗法”的思想来自于他对数论和积分棘手问题的思考；后来掀起孤立子和混沌研究热潮的“非线性分析”，是从他玩弄计算机键盘的手指中开始汩汩流出的。与本文有关系的是，他提出的一种数值方法，宣告了“计算遍历理论”这一集纯粹数学、应用数学和计算数学于一身的学科的诞生。

乌拉姆在20岁时就发表了关于集合论的数学论文，在二战前夕去了美国，从此他那颗天才的大脑为这个国家贡献了许多绝妙的想法，其中有一项对美国政府重要到可以“改变历史的进程”。由于这一巨大贡献他被绝大多数的科学家誉为“氢弹之父”，而许多民众以为匈牙利裔美国理论物理学家特勒（Edward Teller，1908-2003）担当了这一角色，原因是在氢弹从设想到研制成功的整个过程中，后者的社会知名度高于前者。1951年1月23日中午，乌拉姆的太太发现丈夫在家中表情奇怪地凝视着窗外的花园，并说道：“我找到了一个让它工作的途径。”“什么工作？”太太问他。“氢弹”，他回答道，“这是个全然不同的方案，它将改变历史的进程。”连乌拉姆这位能力超凡的“数学科学家”也常惊奇不止地看到，“黑板或草稿纸上的一些乱涂会改变人类发展的进程”。

至于特勒和乌拉姆究竟谁是氢弹的“生父”，他们俩在洛斯阿拉莫斯国家实验室的德裔顶头上司，理论部主任、1967年诺贝尔物理学奖获得者贝特（Hans Bethe，1906-2005）曾有一段妙论：“氢弹制成后，记者开始称特勒为氢弹之父。为了历史，我认为更准确地说，乌拉姆是父亲，因为他提供了种子，特勒是母亲，因为他留在孩子身边。至于我，我想我是助产士。”此处贝特特地将“乌拉姆”的名字用黑体字写出，以示强调。

乌拉姆的提问、方法及猜想

1960年，乌拉姆出版了一本只有150页的小书《数学问题集》。这本薄书却充满了数学思想，成就了许多数学家，约克（James Yorke，1941-）和他的合作者洛速达就是其中的两位。乌拉姆在书中的第六章第四节里问道：“如果将单位区间映到自身的映射S由一个足够‘简单’的函数（例如，逐段线性函数或多项式）定义，其图象不以斜率的绝对值小于1的方式穿过直线y = x，那么它所对应的弗罗贝尼乌斯-佩隆算子有一个非平凡的不变密度函数吗？”接下来乌拉姆举了一族带参数逐段线性映射的例子，对此上述问题的答案那时尚未出现。这族映射S_a定义如下：当0 ≤ x ≤ 1/2时，S_a(x) = 2x；当1/2 < x ≤ 1时，S_a(x) = (2-a) + 2(a-1)x，其中正数a < 1/2。这族映射每个成员的图象斜率绝对值都处处大于1。然而，前面提到的洛速达与麦基合著中的例子说明，“映射图象切线斜率的绝对值处处不小于1”，这个条件还不足以保证不变密度函数的存在性。

十三年后，作为乌拉姆下一代的祖国同胞及“非线性分析”的接棒人，洛速达同他的北美合作者约克在《美国数学会汇刊》（Transactions of the American Mathematical Society）上发表了对乌拉姆如上问题的解答。这是一篇现代遍历理论的重要论文，标题为“关于逐段单调变换不变测度的存在性”（On the existence of invariant measures for piecewise monotonic transformations），摘要仅一句话，简明扼要地概括了文章的贡献：“本文证明区间[0, 1]上一类逐段连续、逐段二次可微的变换有绝对连续不变测度。”在文中他们证明了如下结果：

洛速达-约克定理   若将一区间映到自身的映射S是逐段二次连续可微的，且它的导数的绝对值在该区间上都不小于一个大于1的常数，则S对应的弗罗贝尼乌斯-佩隆算子至少有一个不变密度函数。

特别地，洛速达和约克对乌拉姆书中定义的那族逐段线性映射给出了肯定的答案，即对每一个满足0 < a < 1/2的参数a，映射S_a具有一个绝对连续的不变测度。更进一步，他们的纯粹数学作品又催生出一篇计算数学的创造性文章，作者就是约克的博士李天岩（1945-2020），该文已成计算遍历理论的经典之作。

乌拉姆在《数学问题集》中不仅提出了不变密度函数的存在性问题，也基于概率的思想首次提出了一个计算方法，用来数值逼近已假设存在的不变密度函数。对于给定的映射S: [0, 1] → [0, 1]，乌拉姆先将定义域区间[0, 1]分为n等分，对i = 1, 2, …, n，第i个子区间是[(i-1)/n, i/n]，记为I_i。对每一对指标i, j = 1, 2, …, n，他定义了一个比值p_ij = λ(I_i∩S^-1(I_j))/λ(I_i)，其中的符号“∩”代表两个集合的“交集”运算，即两个集合中共同元素的全体。在p_ij的表达式中，分子是区间I_i与区间I_j在S下的逆像 S^-1(I_j)之交集的勒贝格测度，而分母则是I_i的长度，恒为1/n。因此，p_ij这个数表示第i个子区间I_i中被S映到第j个子区间I_j内的所有那些点在I_i中所占的比例。

用上述的数p_ij作为第i行和第j列的元素，乌拉姆构造了一个n行n列的矩阵，它是映射S所对应的无限维弗罗贝尼乌斯-佩隆算子P_S的一个有限维近似。显然该矩阵的所有元素都是非负数，并且从逆像运算保持交集运算的性质S^-1(A∩B) = S^-1(A)∩ S^-1(B)可知，矩阵每行加起来的和都等于1。这说明乌拉姆定义的这个特殊矩阵是一个随机矩阵，因此学过大学线性代数或矩阵理论的读者就会知道不仅它的谱半径为1，而且1同时也是它的一个特征值。只要计算出其对应的一个非负并被标准化了的左特征向量，即这个特征向量的n个分量之和等于n，那么以这n个分量依次作为对应子区间I₁, I₂, …, I_n上单一常数值的逐段常数函数是一个密度函数，它是P_S的不变密度函数的一个逼近，被乌拉姆称为不变阶梯函数，因为对应于区间剖分的逐段常数函数的图象，很像从侧面看过去的有升有降的阶梯形状。

很自然要问，当映射定义域区间[0, 1]被划分的子区间个数n越来越多，最终趋向于无穷大时，上述乌拉姆设计的算法所获得的不变阶梯函数序列会越来越精确地逼近弗罗贝尼乌斯-佩隆算子P_S的不变密度函数吗？在他的著作《数学问题集》中的第75页上，乌拉姆写道：“我们猜测，如果弗罗贝尼乌斯-佩隆算子具有一个不变密度函数，则当[0, 1]剖分的个数n变成无穷大时，不变阶梯函数将收敛到不变密度函数。”这就是现在所称的“乌拉姆猜想”，而他构造出的这个计算不变密度函数的数值格式也被后人叫作“乌拉姆方法”——现代研究领域“计算遍历理论”以他这本书74-75两页内容为起点，而这是其中最早、也是最著名的算法。 

病中的李天岩首次证明“乌拉姆猜想”

在洛速达和约克证明了他们的上述定理并发表后，一类逐段拉长映射绝对连续不变测度的存在性得到了严格保证。当刚获得博士学位不久的李天岩阅读了他们的论文后，已经对计算数学产生巨大兴趣的他，开始认真考虑如何将理论上保证存在的不变密度函数有效地计算出来。然而，上天对他的身体却没有太眷顾。1974年拿到博士学位之后仅仅六个礼拜，他的血压竟然上升到220/160毫柱，原因是肾脏真的坏了。正如2020年6月25日李天岩教授因病去世后的当天，在我们弟子为他举行的追思会上，他的导师约克教授回忆起他1969年从台湾去了马里兰大学读博士学位后，第二年肾脏就开始出问题，那时他只有25周岁。到了1976年，他的肾功能只剩下一成，遂开始了持续了五年半的肾透析，每周要进行三次，每次要持续五个小时，还不包括花在路上的时间。之后他去了欧洲接受肾移植，却因排斥反应而宣告失败。最终，1981年他一个亲妹妹的肾与他匹配成功，顺利移植，这只无私的肾脏为他工作了39年，也帮助他指导出了26篇博士论文。

李天岩在疾病面前表现出了钢铁般的意志，永不言败，70年代中期那几年，他的许多研究想法是在医院的病榻上构思出的。为了对满足洛速达-约克定理条件的那类区间映射族设计出计算绝对连续不变测度的实用程序，遵循数值分析的一般原则，他先将弗罗贝尼乌斯-佩隆算子离散化。首先他和乌拉姆一样将[0, 1]区间分成n等分，然后他定义了一个值域为有限维子空间的投影算子，它将每一个[0, 1]上的可积函数投影成对应于上述区间剖分的一个逐段常数函数，其在每一个相关子区间上的常数值就是可积函数在这个子区间上的平均值，亦即函数在子区间上的积分除以该子区间的长度。易见，这个投影算子将非负的可积函数投影成非负的阶梯函数，并且保持函数在[0, 1]上的积分不变。

将每个可积函数映到它自己的“单位算子”也是一个投影算子，而且是值域最大的投影算子，因此上述的投影算子成为单位算子的一个有限维逼近。李天岩将它与弗罗贝尼乌斯-佩隆算子复合了起来，这就构成了弗罗贝尼乌斯-佩隆算子的一个有限维逼近。如果限制在区间剖分所确定的全部逐段常数函数所组成的那个n维子空间上，则它的定义域和值域都是同一个子空间，并且在该子空间的标准密度函数基底下，它的矩阵表示是一个随机矩阵。这个基底中的密度函数是所有n个子区间的特征函数除以子区间的长度。那时，李天岩并不知道该矩阵恰好就是乌拉姆在十五年前出版的书中用概率法构造出的那个矩阵。

这时的李天岩对布劳威尔不动点定理情有独钟，因为之前他已经创造出数值逼近这类不动点基于微分拓扑思想的现代同伦延拓法。所以，他并没有采用标准的佩隆-弗罗贝尼乌斯非负矩阵理论，而是将布劳威尔不动点定理直接借来，证明他如此构造的弗罗贝尼乌斯-佩隆算子的有限维逼近算子一定有个非零的不动点，这个不动点是一个逐段常数密度函数。这个结论对区间[0, 1]的任何有限划分都成立，这样他提出的“逐段常数函数投影法”是一个适定的数值方法，即对于任何一个自然数n，该算法都能计算出弗罗贝尼乌斯-佩隆算子的具有立足于n个子区间上阶梯图象的近似不变密度函数。

现在只剩下一个问题需要解决了，但对于计算数学家而言这是最重要的问题，通常也属于最困难的问题：所构造出的适定算法收敛吗？换句话说，对任意自然数n都保证存在的这个近似不变密度函数，当n趋向于无穷大时会收敛吗？此外，如果收敛的话，会收敛到我们希望如此的弗罗贝尼乌斯-佩隆算子的精确不变密度函数吗？

这就需要在洛速达-约克定理的推理细节中寻找帮助证明收敛性的关键线索了，同时也需要挖掘算法提出者自己头脑里贮存的分析数学精华。在洛速达-约克的论文中，约克贡献了一个有用的不等式，它将一个有界变差函数在定义域上的变差与该函数和某个子区间的特征函数乘积的变差之间用不等号建立了一座桥梁。这座桥梁使得这两位合作者获得了关键性的“洛速达-约克变差不等式”，最终引向不变密度函数存在的定理结论。变差是数学分析中的一个重要概念，但我在此略去它的定义，只指出一点：它常在“收敛性分析”中独挑大梁。李天岩敏锐地观察到，他所定义的对应于区间剖分的那个投影算子，不会增加可积函数的变差，这样他借助于洛速达-约克变差不等式的一臂之力，对于满足洛速达-约克定理条件的逐段拉长映射，证明近似不变密度函数的变差对所有的自然数n是一致有界的。再利用分析学中经典的赫利选择定理，所得的逐段常数密度函数序列包含一个子序列在可积函数空间的“范数”意义下，收敛到弗罗贝尼乌斯-佩隆算子的一个不变密度函数。特别地，如果此不变密度函数是唯一的，那么该逐段常数的近似不变密度函数序列将收敛于它。

这是继乌拉姆提出关于不变阶梯函数序列收敛性的“乌拉姆猜想”后，第一次有人对一类具体的区间映射从事关于弗罗贝尼乌斯-佩隆算子的数值分析。它也是李天岩一生三大数学贡献中的一个，并且独立完成， 1976年发表于美国的《逼近论杂志》（Journal of Approximation Theory）。他的另两项贡献可分别简称为“混沌定义”与“同伦算法”，这些都是他30岁前的杰作。然而，到了文章写好为止，他都不知道他所发明的算法与乌拉姆在《数学问题集》一页纸上写出的矩阵本质上别无二致。

文章投稿后，有人告诉作者：你提出的方法就是十五年前问世的乌拉姆方法。不同的是，乌拉姆没有对任何映射族证明过他的方法的收敛性，只是猜测只要不变密度函数理论上存在，算法就收敛。由此看来，李天岩对洛速达-约克区间映射族“意外地”证明了乌拉姆猜想。乌拉姆是闻名世界的数学家，把他的大名放在文章的标题中应该会引来更多潜在的读者。于是，李天岩将自己文章原先的标题“弗罗贝尼乌斯-佩隆算子的有穷维逼近”加长为“弗罗贝尼乌斯-佩隆算子的有穷维逼近：对乌拉姆猜想的一个解答”。从某种意义上讲，李天岩就某类一维区间映射对乌拉姆猜想的证明，复苏了基本上沉寂了十五年之久的乌拉姆方法，他可以与乌拉姆一道被视为计算遍历理论的主要开拓者。

近半个世纪以来，混沌映射不变测度的计算已成为贯穿于数学领域中的遍历理论和工程技术领域中的非线性分析的一个活跃分支。在关于乌拉姆方法及其高阶推广的研究和应用中，乌拉姆的原始著作及李天岩的创新论文几乎成了必不可少的经典文献。

然而，如果区间映射并非是逐段拉长的，即便所对应的弗罗贝尼乌斯-佩隆算子拥有一个不变密度函数，乌拉姆方法的收敛性在一些情形下还没有得到真正的理论保证，或虽然在数值试验中观察到收敛性，却无法给予严格的证明。不过，几十年来，对许多其他范畴的区间映射和高维变换，乌拉姆猜想已获得证明。受到李天岩教授证明方法的启发，本文作者与合作者、中国科学院计算数学与科学工程计算研究所的周爱辉运用多变量函数的变差概念，于上世纪90年代对一类将高维有界区域映到自身的分段扩展变换证明了乌拉姆猜想，而这类变换绝对连续不变测度的存在性在80年代末由两位加拿大数学家证明。

李天岩教授曾对我回忆过他无意中成功求解乌拉姆猜想而引发的内心感叹：“如果我早知道这是与冯·诺伊曼一个级别的数学大家乌拉姆提出的未决问题，或许吓得不敢去碰它。”看来，李教授事先没有读过乌拉姆那本著名的小册子《数学问题集》不一定是个损失，否则他也许真的不敢碰它了。不过，如果读者浏览过我2021年出版的《走出混沌：我与李天岩的数学情缘》一书，了解到他一生读书和治学的经历与经验，大概就会和我一样相信他绝不是一个迷信权威的人，而是直接面对新生的问题，独立自主地思考，想方设法去解决它。如同他对包括我在内的弟子们说过的一句名言所示：“一个问题，大人物解决不了，并不表示小人物也解决不了。”

两种观点看混沌：确定性与统计性

十九世纪末，作为“混沌之祖”，法国数学家庞加莱（Henri Poincaré，1854-1912）在自然科学中首次发现三体问题中的混沌现象；到了七十年后的二十世纪中叶，“混沌之父”洛伦茨（Edward Lorenz，1917-2008）破解了天气预报的“蝴蝶效应”之谜；再过了十五年，由于数学家的洞察力，一个优美的混沌定理横空出世，一个混沌的数学定义破土而出，从此混沌的研究像大海的潮水一波又一波地涌现。“混沌”被众多的科学家认为是二十世纪继“相对论”和“量子力学”之后的第三大科学发现。它的概念、思想、理论和方法早已在物理科学、生命科学及工程科学的许多领域里开花结果。

确定性意义下的混沌揭示出的是自然界的复杂性和多样性，正因为如此，它没有统一的定义，只有通过独特的视角对它刻画，如“从有序和可预测性的枷锁中解脱出来的动力学”、“确定性非线性动力系统的不规则、不可预测的行为”、“某些动力系统复杂的、非周期的吸引轨道”，等等。中国已故的理论物理学家郝柏林（1934-2018）则将混沌看成是“没有周期性的有序”。不管怎样描绘混沌，“对初始条件的敏感依赖性”是混沌的基本特征，这导致动力系统最终性态的不可预测性。

然而在确定性意义下看似杂乱无章的混沌行为在概率统计的意义下又回到了“有规则性”，这不仅提供了研究混沌的新思路和新途径，而且也体现了无序和有序之间的对立统一。中国的概率学家严加安（1941-）用五言诗句，“随机非随意，概率破玄机。无序隐有序，统计解迷离。”精炼描绘出概率统计的养料播撒在确定性系统的大地上结出的丰硕果实。“确定性和统计性”两种观点看混沌，反射出现代数学描写自然界规律的两种相辅相成的合理方式，是必然性与偶然性的有机结合，也是“确定数学与随机数学携手并进共存共荣”这一哲学理念的有力佐证！而现代遍历理论及其计算方法，是研究确定性系统的统计性质的强大武器。

出品：科普中国