每年的3月14日也被称为“ π 日”，这自然是因为 π ≈ 3.14。在与圆相关的场景中，我们总是与 π 这个数学常数不期而遇。不过仔细思考后你可能会发现，我们对 π 这个大名鼎鼎的无理数可谓是既熟悉又陌生：π 是如此重要的数，我们却无法将它写下来；当我们将 π 的精度计算到上亿位之后，仍然不知道这些数字背后是否隐藏着某种规律……

 

撰文 | 伊恩·斯图尔特（Ian Stewart） 译者 | 何生

 

一、Π是什么数？

 

在计算圆的周长和面积时，我们第一次遇到了π。假设圆的半径是 r，那么其周长等于 2πr ，面积等于 πr2 。在几何上，周长和面积这两个量并没有直接关系，所以，在这两个地方都出现了同一个 π，其实是相当不寻常的。有一种直观的方法可以理解为什么会这样：先将圆像匹萨一样分割成许多切片，然后把它们重新组成一个近似于长方形的形状（图1）。这个长方形的宽约等于圆的周长的一半，即πr，而它的高约为r。因此，它的面积可以近似为 πr × r =πr2 。

 

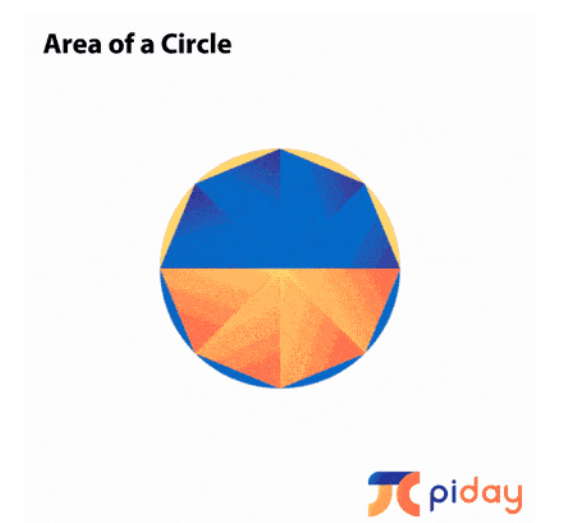
图1. 近似的圆的面积。| 来源：piday.org

 

不过，这只是一种近似。也许，与周长和面积有关的数非常相近，但并不完全相等。然而，这似乎并不可能，因为不管切片分得多细，论证过程总是说得通的。如果我们用大量非常细的切片，近似将变得极其精确。事实上，通过分出任意多的切片，实际的圆和构造出来的长方形之间的误差会变得任意小。利用数学里的极限概念，可以证明这个面积公式是正确且精确的。这就是同一个数会出现在圆的周长和面积里的原因。

 

在这里，取极限的过程也定义了所谓的面积。面积并不像我们想象的那么简单。通过把多边形分割成三角形，可以定义多边形的面积，但是，由曲线构成的图形就不能如此分割。边长是不可公约的长方形的面积，也没那么简单。问题不在于规定“什么是面积”——它只是将相邻两边相乘，难点在于，如何证明计算结果的性质与面积应有的性质是一致的。例如，如果把图形合在一起，那么新图形的面积应该是它们的面积相加的和。学校里教的数学会快速地略过这些问题，并且希望没人会注意到它们。

 

数学家们为什么用一个晦涩的符号来表示一个数呢？为什么不把这个数直接写出来呢？在学校里，我们经常学到 π=22/7 ，但认真的老师会说明它只是近似的。那么，我们为什么不用一个精确的分数来表示 π 呢？因为这样的分数不存在。

 

π 是无理数中最著名的例子。就像根号2一样，无论分数有多复杂，都不能用来精确地表示 π。证明这一点非常难，但数学家们知道如何做到。为此，我们肯定需要一个新符号，因为常规的数字符号无法精确地写出这个特别的数。由于 π 是在整个数学领域里最重要的数之一，因此我们需要有一种方式来明确表示它。这个方式就是用希腊话中“周长”一词的第一个字母“π”。

 

真是造化弄人：π 是如此重要的数，我们却无法写下来，除非用非常复杂的公式。这也许是个麻烦事儿，但它的确迷人，同时也为 π 增添了几分神秘。

 

二、π 和圆

 

我们第一次遇到 π 时，大多与圆有关。圆是一种基本的数学图形，因此，与圆有关的任何事情都是值得知晓的。圆有许许多多有用的应用。2011 年，仅在日常生活的一个方面，圆的使用数量就超过了 50 亿，因为在那一年，全球汽车的保有量超过了里程碑式的 10 亿辆，而当时一辆典型的汽车有 5 个轮子——4 个在跑、1 个备用。（如今，备用的常常是补胎工具包，这样做不仅省油，而且备置起来也更便宜。）当然，从垫圈到方向盘，在汽车里还有许多其他的圆。至于在自行车、卡车、公共汽车、火车、飞机机轮等地方出现的那些圆，则更不在话下。

 

轮子是圆的一种几何应用。轮子被做成圆形，是因为圆上的每个点与中心的距离都相等。如果你在圆形轮胎的中心装上一根轴，它就能在平坦的路面上平稳地滚动。但是，圆还会在别的许多地方出现。池塘里的涟漪是圆的，彩虹的彩色弧线也是圆的（图2和图3）。行星的轨道也大致是圆的——精确一点的说法是，这些轨道是椭圆的，而椭圆是一种在某个方向上被压扁的圆。

 

 

然而，在完全不懂π为何物的情况下，工程师也能很好地设计出轮子。π的真正意义是理论性的，而且非常深奥。数学家们在圆的基本问题里第一次遇到了π。圆的大小可以由三个关系密切的数描述：

 

圆的半径——从圆心到任意圆上的点之间的距离；

 

圆的直径——圆的最大宽度；

 

圆的周长——圆自身整整一圈的长度。

 

其中，半径和直径之间的关系很简单：直径是半径的 2 倍，半径是直径的一半。

 

周长和直径之间的关系就没那么简单了。如果在圆上画一个内接正六边形，会让人觉得圆的周长要比直径的 3 倍更长一些。在图4中有6条半径，每两条配在一起后可以得到3条直径。正六边形的周长与6条半径相等，也就是3条直径的长度。很明显，圆的周长要比正六边形的周长更长。

 

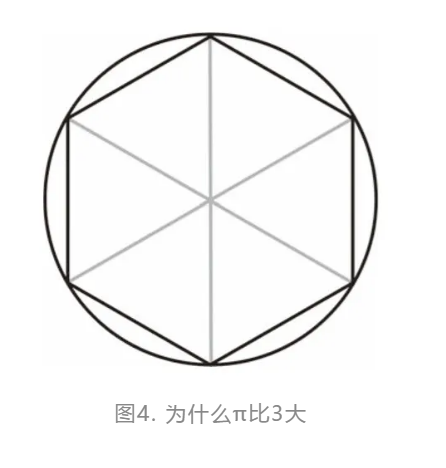
π 的定义是：圆的周长除以它的直径。无论圆有多大，这个数的值都是一样的，因为圆形在放大或缩小时，其周长和直径保持相同的比例。大约在 2200 年前，阿基米德给出了一个完整的逻辑证明，证明指出，对于任意的圆而言，这个数是一样的。

 

 

 

 

图5. 阿基米德通过构造圆的内接多边形和外切多边形来逼近π的下界和上界。| 来源：piday.org

 

π 的前 1000 位是：

 

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420199

 

看看这些数字，它们最显著的特点就是完全没有规律。这些数字看起来是随机的，但事实上不可能，因为它们是 π 各个数位上的数字，而 π 本身是一个特定的数。缺乏规律性，更让 π 这个数显得异常奇特。数学家们猜测，所有有限长度的数字串都会出现在以小数表示的 π 的某个位置上，甚至会无限多次出现。事实上，人们猜测 π 是一个正规数，即所有给定长度的数字串会以相同频率在其中出现。这些猜想尚未被证明或证否。

 

三、无穷级数中的 π

 

π 也会出现在其他数学领域里。这些领域与圆之间往往没有明显的联系，但总会存在某个间接联系，因为这中间产生了π。同时，这也是其他定义π的方式。因为所有定义都必须得到同一个数，因此，沿着这条线索必然会证明出与圆有关的关系。但是，这种关系可能非常曲折。

 

例如，欧拉在 1784 年发现了数 π、e 和 i（即 - 1 的平方根）之间的关系。这个优雅的公式是：

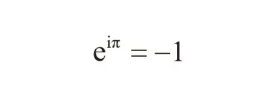
欧拉还注意到，对某些无穷级数求和也能得到 π。1735 年，他解决了巴塞尔问题。这个问题是由彼得罗·门戈利在1644年提出的，旨在计算所有平方数的倒数之和。当时，曾有许多伟大的数学家试着去计算，但都没成功。欧拉在 1735 年算出了一个相当简洁的结果：

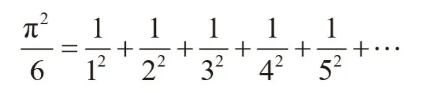
这一发现让欧拉在数学界声名鹊起。你能说出它和圆之间的关联吗？反正我是不知道。其中的联系不可能很直观，因为很多顶尖数学家都无法解决巴塞尔问题。实际上，它和正弦函数有关，但第一眼看上去，正弦函数与这个问题也没什么联系。

 

对四次方、六次方，乃至更一般的偶数次方而言，利用欧拉的方法可以得到类似的结论。例如，

 

 

但是，对像三次方和五次方等奇数次方而言，则没有类似的公式，而且，人们猜想这样的公式根本不存在。

 

值得注意的是，这些级数及其相关问题与质数和数论之间有着很深的联系。例如，如果随机选取两个整数，那么它们没有（大于1的）公因数的概率是：

 

这条曲线下方的面积正好等于根号π （图6）。

 

许多数学物理方程也和 π 有关。数学家们还发现了大量具有 π 的显著特征的方程。

 

 

四、如何计算π？

 

2013 年，在经过 94 天的计算之后，近藤茂利用计算机将π算到了12 100 000 000 050 位小数——超过了 12 万亿位。实际使用的π并不需要这种级别的精度。你也不可能用它来测量真实的圆。多年以来，人们有许多计算π的方法，它们都基于 π 的公式，或是如今用公式表示出的各种过程。

 

人们热衷于做这类计算，他们的理由是为了了解这些公式的表现情况，或者确认新计算机的性能。但实际上，大家更多是为了打破纪录。一些数学家沉迷于计算π的更多位数，只是因为它们“存在”，这就好像山峰与登山者之间的关系。这种痴迷于“打破纪录”的行为并不是典型的数学研究，其本身几乎没什么意义和实用价值，但通过这类活动，人们发现了一些全新的迷人公式，并揭示出了数学和其他领域之间一些意想不到的联系。

 

（1）π 作为极限

 

通常，π的公式都涉及无穷的过程，只要执行的次数足够多，π就能得到很好的近似值。继阿基米德之后，人们在15世纪首次取得了进步。当时，古印度数学家用无穷级数之和来表示 π，这是一种将各项不断累加的求和过程。如果级数总和的值越来越接近一个明确的数（即它的极限），那么它就可以用来计算越来越精确的近似值，比如这些公式就是如此。一旦所需的精度得到满足，那么计算就可以停止。

 

1400 年左右，桑加马格拉玛的玛达瓦利用一种级数把π计算到 11 位。1424 年，波斯人贾姆希德·卡希对它做了改进，他像阿基米德那样，采用增加多边形的边数的方法做近似。卡希通过计算 3 × 228 边形，得到了 π 的前16 位。

 

 

1641 年，詹姆斯·格雷戈里重新发现了玛达瓦用于计算π的一种级数。格雷戈里的主要思路是用三角函数里的正切函数，记作 y = tan x 。在弧度表示法里，45° 角等于 π/4， 此时 a = b，因此有 tan (π/4) = 1 （图7）。

 

 

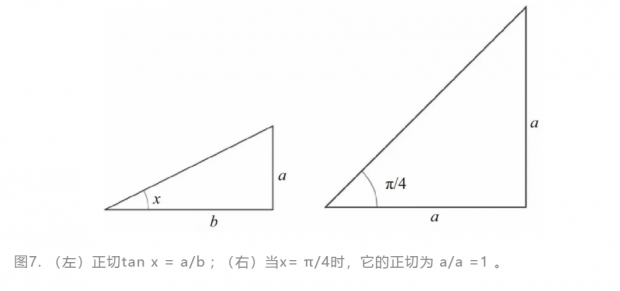
现在，让我们考虑正切函数的反函数，通常被记为 y = arctan x 。它表示“还原”正切函数，也就是说，如果 y = tan x ，那么 x = arctan y ，因此有arctan1 =π/4 。玛达瓦和格雷戈里发现了关于 arctan y 的无穷级数：

 

 

接着，他把 1/5 和 1/239 代入表示 arctan x 的级数。这些数字比1小很多，因此级数收敛得很快，也更实用。马钦用他的公式将π计算到100位。1946年，丹尼尔·弗格森将这种思想推到极致，他采用了一个类似却又不一样的公式，将π计算到620位。

 

马钦的公式还有许多精致的变体，事实上，这类公式有一套完整的理论。1896 年，F. 施特默发现了公式：

 

 

其每项都能贡献14位新小数。在这里，求和记号∑代表对k的表达式求和，其中k等于从0开始的所有整数。

 

（2）二进制表示中的 π

 

还有许多其他计算π的方法，并且新方法还在不断地被发现。1997年，法布里斯·贝拉尔公布了π的第一万亿位小数，这个数用二进制表示的话是1。令人惊讶的是，贝拉尔并没有计算前面的数字。1996 年，戴维·贝利、彼得·博温和西蒙·普劳夫发现了一个很奇妙的公式：

 

 

通过熟练地分析可知，这一方法可以给出单个位数上的二进制数值。公式的关键特征是，其中的许多数，如 4、32、64、256、 24n 和 210n ，都是2的指数次方，它们可以非常简单地在计算机内部使用二进制表达。寻找 π单个位数上的二进制数值，这一纪录很容易被打破：2010 年，雅虎的施子和计算了π的第 2000 万亿位小数，其结果是 0。

 

这个公式还可以被用于单独计算基底为 4、8 和 16 的 π 的单个位数上的数值。基于其他基底的公式尚未被发现。尤其是，我们无法单独计算十进制 π 的单个位数上的数值。这类公式存在吗？在贝利–博温–普劳夫公式发现之前，也没人觉得在二进制里会有可以计算单个位数上的值的公式。

 

五、“化圆为方”可能吗？

 

古希腊人寻找过一种化圆为方的几何作图法。所谓“化圆为方”是指已知圆形的面积，求作与其面积相同的正方形的边。人们最终证明，它和三等分角和倍立方体一样，仅用尺规作图是无法做到的。证明的关键是知道π是哪种数。

 

我们已经知道，π不是有理数。有理数的下一类是代数数，它满足系数是整数的多项式方程。例如，是代数数，它满足方程 x2 = 2。不是代数数的实数被称为超越数，而第一个证明了π是无理数的兰贝特在1761年猜测，π实际上是超越数。

 

时隔112 年，查尔斯·埃尔米特于1873 年在这个问题上取得了第一次重大突破，他证明了，在数学里的另一个奇妙数——自然对数的底e是超越数。1882年，费迪南德·冯·林德曼通过改进埃尔米特的方法，证明了如果一个非零数是代数数，那么e的该数次方也是超越数。接着，他利用了欧拉公式，即eiπ =−1 。如果π 是代数数，那么iπ 也是。因此，根据林德曼定理可知，−1不满足代数方程。然而，它显然是满足代数方程的，如方程 x+1= 0。唯一避免这一逻辑矛盾的方法就是，π不满足代数方程，也就是说，它是超越数。

 

这个定理带来的一个重要影响就是，它解答了化圆为方这个古代几何问题。该问题讨论了，如何只用直尺和圆规构造一个与圆形面积相同的正方形。这等价于利用长度为1 的线段构造出长度为π的线段。根据解析几何，用这种方法构造出来的数必须是代数数。由于π不是代数数，所以这种构造方法不存在。

 

但是，即便在今天，这一结论并没有让某些人停止寻找尺规作图的方法。这些人似乎不明白，数学上的“不可能”意味着什么。这个困惑长久以来一直存在。1872 年，德摩根写了一部名为《悖论集》（A Budget of Paradoxes）的著作，他在书中指出了许多所谓“化圆为方”方法的错误，并把它们比作成群的苍蝇在大象周围飞舞，嗡嗡地叫着“我比你大”。但在 1992 年，安德伍德·达德利在《数学狂怪》（Mathematical Cranks）一书里仍继续着尺规作图的任务。他想尽办法用其他工具探索如何在几何上近似π，希望找到构造它的方法。但请你明白，严格来说，传统意义上的尺规作图方法是不存在的。

 

 

本文经授权选自《不可思议的数》，略有修改。

 

作者简介

 

伊恩·斯图尔特（Ian Stewart），数学家，英国皇家学会会员，曾获英国皇家学会的“法拉第奖章”。他著有多部优秀的畅销数学科普作品，如《改变世界的十七个方程》《数学万花筒》系列等。

 

版权说明：欢迎个人转发，任何形式的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。