夫人之相与，俯仰一世，或取诸怀抱，

悟言一室之内；或因寄所托，放浪形骸之外。

虽趣舍万殊，静躁不同，当其欣于所遇，

暂得于己，快然自足，不知老之将至。

 

——王羲之《兰亭集序》

 

 

撰文 | 许霄琰、孟子杨

 

01 引 子

 

人的一辈子，乱乱哄哄、热热闹闹，其实很快就过去了。浮名与虚誉、诱惑与利益，很多时候更是在加速这个过程。时间积分之后，烦恼总是大于欢欣的。这样一个悖论，古今中外多少人都看得明白，比如大书法家王羲之，其所言如上所抄录很是通透。

 

但看明白之后，又该怎么求解脱呢？宗教总是一个选择，更加起劲地追逐名利也是一个办法。还有的人，其中艺术家、科学家居多，选择给自己找一个足够抽象的动机，然后认真地去思考和追寻一个科学上、艺术上的难题。很多时候，就算一辈子也解决不了这道难题，但这样抽象地追寻的本身就变成了支撑自己、鼓励同伴的理由。幸运的话，追寻的路上偶尔就能经历“欣于所遇，暂得于己，快然自足，不知老之将至”的片刻。如此，该是多大的欢乐与满足！

 

我们在量子多体晶格模型的蒙特卡洛计算中追寻非费米液体的努力，多少有这样一些意思。这样的系列研究，已经有数篇科研论文问世：从 2017 年的巡游铁磁量子临界点[1]，到自学习量子蒙特卡洛方法[2]，再到 2019 年的鸸鹋量子蒙特卡洛方法[3]，及至巡游反铁磁量子临界点[4]，如此等等。这一次，我们关于巡游铁磁量子临界点上非费米液体自能行为的工作，有幸以“Identification of non - Fermi liquid fermionic self - energy from quantum Monte Carlo data”为题在《npj Quantum Materials》刊物上发表[5] (点击文尾之阅读原文处)。文章投稿过程顺利，在刊物编辑认真负责的态度下，我们得以与审稿人同行进行了深入地交流，颇有所获。及后，又承蒙主编 Ising 君的诚意邀请，得以写一篇简短的中文介绍，讲讲这个让我们快然自足的故事。

 

02 费米液体理论的是非

 

关于非费米液体的基本知识，很遗憾无法三言两语可以梳理清晰。非费米液体与朗道费米液体理论的联系，还有非费米液体在现代凝聚态物理学量子多体问题中的内涵与外延，笔者在之前的文章中有过通俗的铺垫性介绍，见文献[6, 7]，也可以分别点击《白马非马》和《一生能有多少爱》间隔御览。对细节感兴趣的读者诸君，则尽可以标记起来，即便是床前厕上都可以无障碍地愉快阅读^_^。

 

进入正题。我们知道，朗道费米液体的基本特征可以借助自由费米子模型来理解。在自由费米子模型中，受 Pauli 不相容原理限制，无相互作用费米子填充能量低于 EF (费米能) 的能级。从动量空间看，即填满波矢小于 kF  (费米波矢) 的波矢面 (费米面)。系统低能激发包含粒子型 (费米面外) 和空穴型 (费米面里) 的准粒子激发。这个图像看起来并不复杂，且的确得到广泛应用。

 

朗道费米液体理论认为，即便考虑费米子间相互作用，这种简洁的物理图像依然成立。也就是说，相互作用不会破坏准粒子的图像，而只是修正准粒子的波函数、减小准粒子权重而已。的确，费米液体理论成功描述了大多数简单金属低温下的行为，例如有限的准粒子权重、电阻和温度平方成正比、比热和温度成正比，等等。这些成功某种程度上印证了上述说法：费米液体理论很强大！

 

但是，近几十年来，也的确发现了许许多多的反例。在重费米子、过渡金属和非常规超导等研究中，的确出现了很多奇怪的金属行为。例如，电阻不再和温度平方成正比，而是与温度的 α 次方成正比 (α < 2)。这些奇怪的金属行为被称为奇异金属 (strange metal)，又通常称为非费米液体行为。虽然说是奇异，但实际上很常见，说明费米液体理论并非四海而皆准的道理。

 

理论上，非费米液体可能出现在相互作用驱动的金属-绝缘体相变边界上，也可能就是低能玻色型涨落与费米子耦合所制造的量子临界金属态。前者有行家里手多年浸染，而后者物理则更为丰富，可以作为量子相变中最富挑战性的例子和量子物质科学超越朗道-金兹伯格的新范式的起点。正因为如此，我们对这一问题尤为关注。

 

例如，考虑 (2 + 1) 维量子临界系统中的费米面，让费米子与临界铁磁玻色场耦合，玻色场本身由 ϕ4 模型描述。如果能够调节玻色场有效质量为 0，系统就将处于一个铁磁量子临界点上。理论计算发现，此时系统处于非费米液体状态，费米面上不再有准粒子，即准粒子权重为零。这里，准粒子权重 Z 可由费米子的自能 Σ(ω) 给出：

 

Z = { 1 + ∂[ReΣ(ω)] / ∂ω |ω→0}-1 

 

为了叙述的通畅，相比通常的定义，这里自能吃进了一个负号。

 

众所周知，自能刻画了费米子之间的相互作用，满足幂指数的形式，Σ(ω) ~ ωα。对于费米液体，α = 2；对于非费米液体，α < 1。在能量接近费米面的时候，即 ω → 0 时，可以看到费米液体的准粒子权重接近 1。而对非费米液体，由于自能求导发散，准粒子权重就变成了 0。可见，确定自能的形式，也就确定了准粒子权重的大小，从而可以判断一个体系是否为非费米液体。

 

我们回到 (2 + 1) 维铁磁量子临界点例子的具体理论计算。考虑单圈微扰论，理论计算给出的费米子自能形式与频率的关系为 Σ(ω) ~ ω2/3。而多圈计算，通过量纲分析，也可以重复得出该 2/3 幂律。这里需要指出的是，刚开始人们做 large- N 计算时，就以为这一微扰是收敛的。因此从理论上来说，这一微扰论结果似乎已经很完美。我们这篇 npj Quantum Materials 文章 [5] 的合作者、明尼苏达大学的 Andrey Chubukov 教授，正是非费米液体圈图计算方面的集大成者。他作为俄国朗道学派的后人，为本领域的发展做出了许多奠基性的工作。

 

但是，2009 年，加拿大 McMaster 大学的 Sung - Sik Lee 通过理论计算发现：存在一类“planar diagrams”，尽管仍然给出 2/3 幂律，但 large - N 却并不收敛[8]。后来，哈佛大学的 Max Metlitski 和 Subir Sachdev 基于三圈图计算和四圈图的论证也发现，不仅仅 large - N 不收敛，2/3 幂律也存在对数修正项[9]。所以，对于非费米液体这样的量子多体问题，解析的微扰论圈图计算其实也有一些本征缺陷。

 

既然微扰计算不收敛，那么这类非费米液体的自能形式究竟是怎样，目前并无定论，需要严格的晶格模型数值计算来提供答案。但遗憾的是，这方面的研究一直是空白。造成这种现象的原因很多，但从数值计算物理学家本身来看，理论修养的不足是一大原因。

 

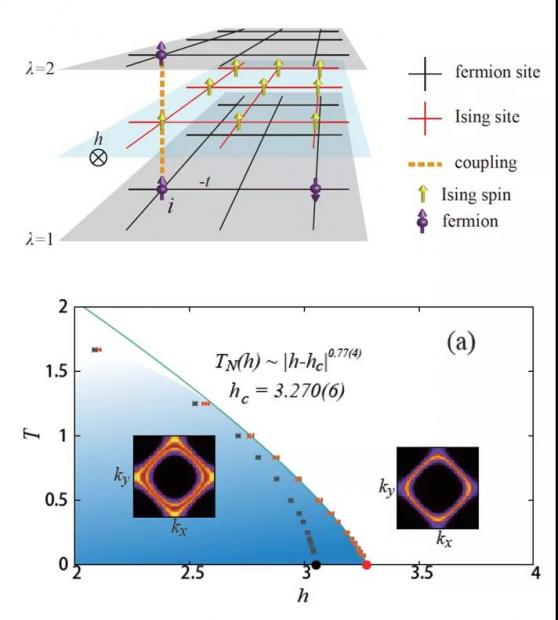
图1．(上) 费米子与铁磁量子 Ising 自旋耦合模型 [1]。λ = 1, 2 表示正方晶格的两层自由费米子，中间一层为量子 Ising 自旋。自旋之间具有铁磁相互作用，横向的磁场 h 引入 Ising 自旋的量子涨落。涨落通过耦合传递给费米子，引入费米子之间的有效相互作用。(下) 量子蒙特卡洛计算得到的费米子与铁磁量子 Ising 自旋耦合模型相图。

 

03 风华晨露

 

当然，计算物理学者的理论修养稍有欠缺当属情理之中，否则纯粹理论学者的地位就岌岌可危了。而近几年来，鉴于凝聚态物理学量子多体问题研究的需要，这种修养不足正在得到部分弥补。现在的多体物理领域，正慢慢涌现出一个趋势，那就是从事数值计算的学者与从事解析理论的学者通过良性互动、彼此提高，各自变成了懂得量子多体计算的理论学者和懂得量子多体理论前沿的计算学者。这些复合型人才和他们新的研究模式，正在变成主流，并孕育着汹涌澎湃。

 

随着数值计算凝聚态学者自身理论修养的提高，近几年来陆续提出了很多没有负符号问题的晶格模型。通过量子蒙特卡洛方法，对费米子与玻色场耦合模型进行大规模模拟，从中寻找非费米液体行为，并研究它们的性质。图 1 所示即为一例，这是我们设计的铁磁量子临界点模型和蒙特卡洛计算得到的相图[1]。然而，令人有些窘迫的是：数值计算得到的费米子自能形式似乎与理论上可能的 2/3 幂律差之甚远。具体来说，数值上得到的低频下费米子自能趋于常数、甚至有发散的迹象。这与 2/3 幂律要求趋于零的结果截然不同。

 

对 Ising 铁磁涨落与费米子耦合模型，我们计算了量子临界点处的费米子自能，也发现偏离 2/3 幂律的缓慢发散迹象，如图 2(b) 所示。这样的行为在当时并不能够理解。

 

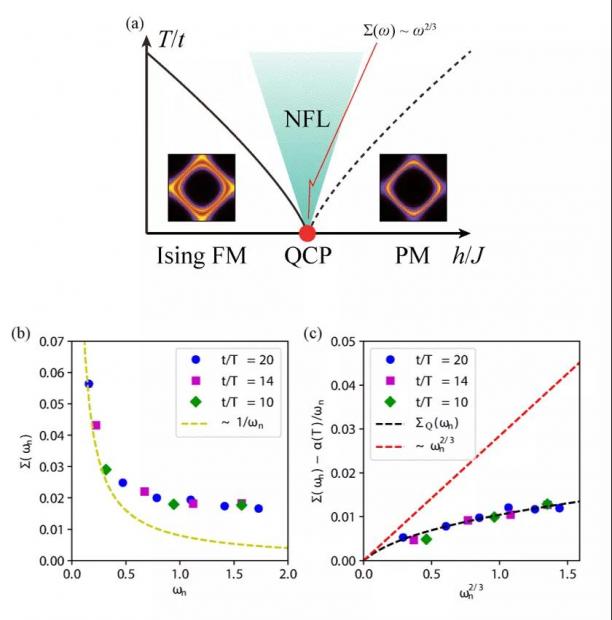
图2. Ising 铁磁量子临界点上的非费米液体行为。(a) Ising 铁磁涨落与费米子耦合模型的相图。(b) 相变点上的费米子自能。(c) 减去热贡献部分自能后，剩余部分的自能可以很好的被单圈理论计算描述，并且在低频逼近 2/3 幂律行为。

 

最近，正是通过与 Andrey Chubukov 等人讨论，我们得知：有限温度涨落对低频自能行为有很大修正。这种修正似乎为解释数值计算中得到的奇怪自能行为提供了方向。在解析计算方面，以往都是直接在零温下进行计算，所以理论学者没有想到有人可以设计出我们这样的晶格模型，然后计算带有温度效应的自能。也因为如此，理论学者也就没有认真研究过热涨落对量子临界自能的贡献。如此认识，正是解决问题的关键，也是前文提到的从事数值计算的学者与从事解析理论的学者通过良性互动、彼此提高的一个例子。

 

就是在这样的共识下，我们与 Andrey Chubukov、他的博士后 Avraham Klein 和密歇根大学的孙锴 (系列文章 [1-5] 的长期合作伙伴) 一起，决定从解析和数值两个方面开始一项合作研究。我们提出了一种能够分开自能中热涨落贡献和量子涨落贡献的方法。这一方法的理论认识主要基于三个观察：

 

(1) 费米子和玻色场耦合强度远小于费米能，即体系处于弱耦合；

(2) 费米子自能远小于松原频率，此时费米子自能中热涨落贡献可以近似由 α(T )/ωn 来描述；

(3) 费米子自能中量子涨落贡献具有非费米液体的形式，可由单圈计算近似给出，在扣除热涨落之后便可看到。

 

基于这三个观察，我们可以将费米子自能表示为 Σ(ωn)= α(T )/ωn + ΣQ(ωn)。其中，ΣQ(ωn) 为量子涨落贡献部分，可由单圈计算近似给出，并且在低频下的确具有 2/3 幂律的渐进行为。进一步，将这一模型带入到我们考察的铁磁量子临界模型中，关注于量子临界点上的费米子自能数据。在解析计算出热涨落部分的贡献 (当然需要蒙特卡洛模型参数作为输入) 后，扣除热涨落 α(T ) / ωn 的贡献，剩余的自能就展现出量子临界行为应该有的样子，如图 2(c) 中黑色虚线和附近的数据所示。毫无疑问，在接近零温区域，2/3 幂律的渐进行为依然很完美地展现出来。

 

如此的分析告诉人们，事实上在蒙特卡洛计算中，已经可以清楚地从量子临界区看到非费米液体的自能，关键在于如何正确地设计模型和分析数据。这种分开自能中热涨落贡献和量子涨落贡献的方法似乎是普适的。我们最近在一个完全不同的模型研究中，也发现了类似的自能行为，并进一步验证了该方法的适用性。

 

04 并非结语

 

现在看来，对于铁磁量子临界点上的非费米液体自能，通过扣除掉有限温度自能的热涨落贡献，就可以明确地揭示出非费米液体的自能及其分数化幂律的渐进行为。这一结果还只是一个开始，接下来，对于其它的量子临界涨落模型模型，如反铁磁、电荷密度波、规范场涨落等，都可以进行类似设计和量子蒙特卡洛计算。由此，结合理论与数值分析，逐步建立起如费米液体一般的非费米液体理论框架。这一物理图像，看起来更像一个量子物质科学的新范式。对于费米子量子临界点、高温超导现象中的 strange metal 等凝聚态物理学中未解之谜，这一范式也许可以给出确定性答案。

 

行文至此，我们的体会是：这一过去一直不解的根源，其实并非那么复杂和遥不可及。对于非费米液体这样的难题，很多情况下，至少对于量子临界点处，其自能的行为也有章可循。受此激励，我们将一路追寻下去，并相信下一个快然自足的片刻可能明天就会到来。

 

 

参考文献

[1] Xiao Yan Xu, Kai Sun, Yoni Schattner, Erez Berg, Zi Yang Meng, Non-Fermi - liquid at (2+1)d ferromagnetic quantum critical point, Phys. Rev. X 7, 031058 (2017).

 

[2] Xiao Yan Xu, Yang Qi, Junwei Liu, Liang Fu, Zi Yang Meng, Self - learning quantum Monte Carlo method in interacting fermion systems, Phys. Rev. B 96, 041119(R) (2017).

[3] Zi Hong Liu, Xiao Yan Xu, Yang Qi, Kai Sun, Zi Yang Meng, EMUS-QMC: Elective momentum ultra - size quantum Monte Carlo method, Phys. Rev. B 99, 085114 (2019).

[4] Zi Hong Liu, Gaopei Pan, Xiao Yan Xu, Kai Sun, Zi Yang Meng, Itinerant quantum critical point with Fermion pockets and hot spots, PNAS 116, 16760 - 16767 (2019).

[5] Xiao Yan Xu, Avraham Klein, Kai Sun, Andrey V. Chubukov, Zi Yang Meng, Identification of non-Fermi liquid fermionic self-energy from quantum Monte Carlo data, npj Quantum Materials 5, 65 (2020).

[6] 白马非马，非费米液体—非—费米液体 | 量子多体中的呐喊与彷徨之二，

https://mp.weixin.qq.com/s/YbKUoBUd1nZY3vArHXtNag

[7] 一生能有多少爱 | 量子多体中的呐喊与彷徨之三，

https://mp.weixin.qq.com/s/snExMJ9SsenJw1JToggezQ

[8] Sung-Sik Lee, Low - energy effective theory of Fermi surface coupled with U(1) gauge field in 2+1 dimensions, Phys. Rev. B 80, 165102 (2009).

[9] Max A. Metlitski and Subir Sachdev, Quantum phase transitions of metals in two spatial dimensions. I. Ising-nematic order, Phys. Rev. B 82, 075127 (2010).

 

备注

(1)   笔者许霄琰，目前为加州大学圣地亚哥分校博士后。

(2)   笔者孟子杨，目前供职于香港大学/中科院物理所。

(3)   封面图片《兰亭曲水图》，来源 Wikipedia (https://zh.wikipedia.org/wiki/流觞曲水#)，寓意科学和艺术的创造性活动中快然自足的境界，虽不能至、心向往之。

 

本文经授权转载自微信公众号“量子材料QuantumMaterials”。