0.999...到底等不等于1？-返朴的财新博客-财新网

撰文 | 杨浩

如何严谨地证明0.999...=1？

知乎上有一个数学问题引发了大家的讨论——“如何严谨地证明？关于此问题的回答也是五花八门，各抒己见。这个问题的有趣之处在于不同数学水平的人会有不同的理解。

为了后面能够把这个问题讨论清楚，我们先整理了几个知乎上的高人气“抖聪明”答案。

答案一：

根据人教版小学四年级下册教材：“如何比较小数的大小？先比较整数部分，整数部分越大，小数越大；整数部分相同的，再比较小数部分……”，显然 " "，二者并不相等。

上述几种方法分别代表了小学、初中、高中数学知识水平，在一定的知识能力范围内，这些证明似乎都正确。

那么，到底哪个才是足够严谨的证明？

与是不是真的相等？这就要追溯到几百年来数学家们对无穷小量的探讨之中。

无穷小量的产生

无穷小量的产生来源于17世纪微积分的创立。微积分的诞生首先是为了解决一系列自然科学的问题（求瞬时变化率、求曲线的切线等等），牛顿（Isaac Newton, 1643-1727）和莱布尼兹（ Gottfried Wilhelm Leibniz, 1646-1716）先后独立地建立了微积分理论体系。

1669年牛顿在《运用无穷多项方程的分析学》一书中初次提出了他的想法（这本书直到1711年才出版）。

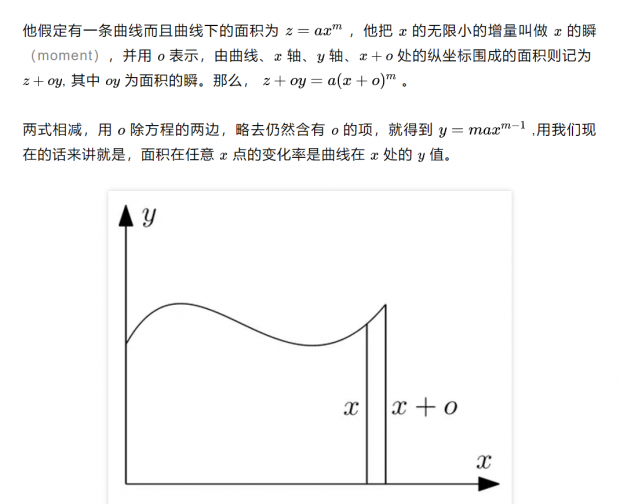
莱布尼兹也推出了同样的结果。

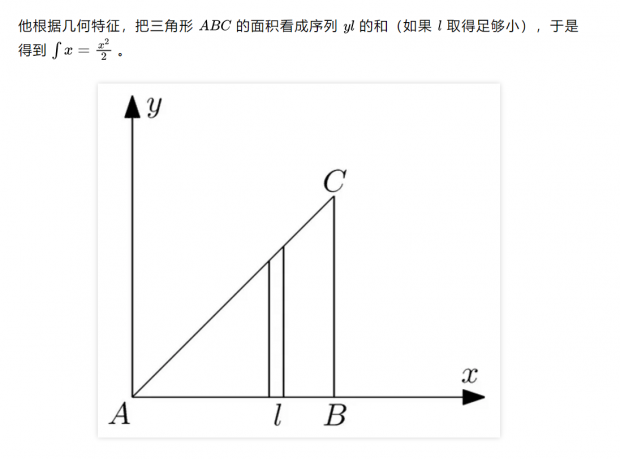
牛顿和莱布尼兹都使用了无穷小的方法，尽管后来微积分迅速普及并且被广泛地使用，但也掩盖不了这种方法在逻辑上的不严密。

由于无穷小量（无论是牛顿的，还是莱布尼兹的）没有被明确的定义，很快，微积分就迎来了一系列质疑的声音——无穷小量和到底有怎样的区别？推理过程中为什么能够直接舍弃无穷小量，而无穷小量的和却可以是有限的量？

针对这些疑问，牛顿和莱布尼兹意识到微积分存在的问题，也各自作出了回应。

1671年，牛顿阐述：变量是由点、线、面的连续运动产生的。1676年，他又说，流数（变量的变化率）是增量的最初比。

莱布尼兹在1690年写给沃利斯的信中说：“考虑这样一种无穷小量将是有用的，当寻找他们的比时，不把它们当做是零，但是只要它们和无法相比的大量一起出现，就把它们舍弃……”

可以看出，他们试图把自己的理论说清楚，但无穷小量的确切含义，仍然十分模糊。

无穷小量的争议与解决

18世纪初，微积分的不严密性招致了教会的攻击。由于害怕机械论和决定论对宗教的威胁，英国大主教贝克莱于1734年发表《分析学者》一文抨击牛顿是 “依靠双重的错误得到了虽然不科学却是正确的结果”。

数学家们当然不能容忍这种对数学的轻蔑，他们立即加入了争论，并且继续尝试给微积分提供严密的基础，虽然大部分都失败了，但我们不能否认的是，在得到正确的结果之前，有一些数学家的贡献是不可忽视的。

沃利斯在《无穷的算术》中，提出了函数极限的概念，产生了新思想的萌芽。

欧拉则是把微积分从几何中解放出来，而使它建立在算术和代数的基础上，为基于实数系统的微积分的根本论证开辟了道路。

进而，导数、积分、收敛性、无穷级数等概念一一被严格确定下来，关于无穷小量的长达两个多世纪的争论（也称第二次数学危机）终于结束。

但这并不是基础研究的终点，所有相关的研究工作都是以承认实数系为先决条件的，而实数系的逻辑基础到19世纪后半叶才逐渐建立起来。实数系的建立者是康托尔（同时建立了集合论），在有理数系的基础上，他引入了一个新的数类——实数。

如今，实数理论进一步发展为实变函数论，已经成为微积分的一个重要分支，实变函数也是数学专业大学生的主要课程之一。

无穷小量、极限和高中数学的关系

现在我们可以发现的问题，本质上是数学基础的问题，它反映了实数的稠密性和完备性。

对于任意正有理数，都有，于是根据康托尔对实数的定义，与就是同一个实数。

换句话说，如果这两个数不相等，那么实数理论，以及建立在实数系基础之上的微积分的大厦将会崩塌。

在高中阶段，我们也会学习简单的微积分知识，比如导数和定积分的运算，在数学中，我们可以运用导数解决函数的最值问题；在物理中，可以根据位移函数求瞬时速度和加速度，也可以解决简单的天体物理运动问题。

因此，高中数学课本中对导数的解释其实是有些模糊不清的，事实上，到大学数学分析中，我们才能学到函数的连续性、导数、积分最明确、严谨的定义。数学是最讲逻辑的学科，数学家们花了近3个世纪，才把微积分的理论从建立到完善，甚至直到今天，还有一些悬而未决的问题。

相信大家看完文章后，也会对微积分、对数学有全新的认识，直观感受有时也会导致错误的结果。我们以后在思考问题的过程中，也要争取像数学家们一样，力求严谨，不能似是而非。

本文经授权转载自微信公众号“新东方智慧学堂”。原标题为《0.999...到底等不等于1？400多个知乎回答，都不算对》。

话题：