阅读：0
听报道
撰文 | 贝爽、陈大鑫
视频作者 | B站@Ele实验室
本文经视频作者授权整理成图文版
要说在《三体》这本著名的科幻小说中挑选几个令人印象深刻、血脉膨胀的科幻元素和场景，那水滴攻击和二向箔降维打击肯定能上榜。
图注：水滴
今天我们就来讲一讲降维打击——如何实现对地球“从三维向二维跌落”。
在《三体》中，太阳系被一小片二向箔攻击由三维降至二维的场景描述实在是太吸引人了有没有：
“这是第一个跌入二维的固态行星，与海王星和土星相比，二维地球的“年轻”更加清晰精致....”，听起来如此有诗意的描述，激发了不少读者的无限想象，一位重度科幻迷的B站Up主Ele实验室便是其中一个，起初他想象的三体降维是这样的：
啪的一声！三维变成可二维...
啊这... 有点儿草率了。
那下面这样呢？
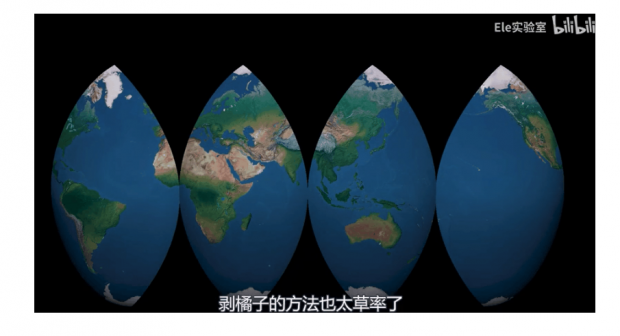
这种剥橘子的方法显然也不太行。
其实，以上这两种想法最大的问题就是只考虑了地球的表面。就像我们在玩游戏穿模时看到的那样，目前主流的三维建模技术采用的都是三角面，组成物体的表面，而至于物体的内部则只是空的而已。
但地球其实是一个实心的球体，从内到外依次是地核、地幔、地壳和地表。
这就有点复杂了。
那么该如何实现对三维物体降维攻击呢？
几天前，这位B站UP主在用threejs框架编写程序时，无意间发现了一个Demo，
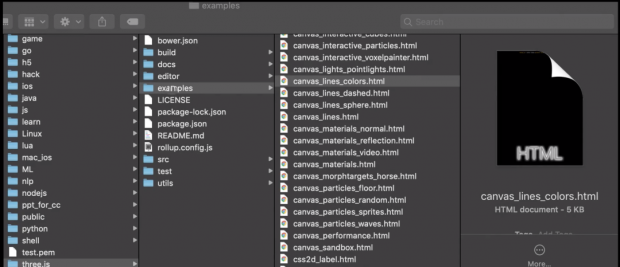
它大概这个样子：
和大多数人一样，Up主起初也以为这个密集恐惧者看了流泪、贪吃蛇爱好者见了狂喜的线条，只是一个简单的数学分析。
但研究之后，他发现这其实是大名鼎鼎的希尔伯特曲线。
正是借助这条曲线，Up主成功实现了对三体的降维打击。
希尔伯特曲线
我们先来了解一下什么是“希尔伯特曲线”？
早在19世纪时数学界就掀起了一阵用一维直线填满二维平面的热潮，换句话说就是找到一维和二维的一个映射，起初是意大利数学家皮亚诺，没错，就是时不时出现在高等数学教材里的老伙计：
他提出了一种能够填满平面的曲线皮亚诺曲线，紧接着是德国数学家希尔伯特提出了另外一种希尔伯特曲线，这也就是本文要介绍的Up主用来完成降维打击的工具。
希尔伯特曲线是这样的：这是一个平面正方形，先把它画为4等份，可以使用这样一条曲线遍历所有的四个小块，这就是一阶的希尔伯特曲线。
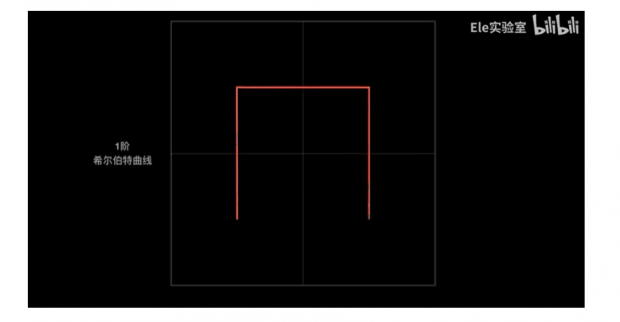
之后每个小块可以再划分为4等份。如果还想得到一个能够遍历出所有小块的曲线，可先把4个小区域内各自画出一阶希尔伯特曲线。
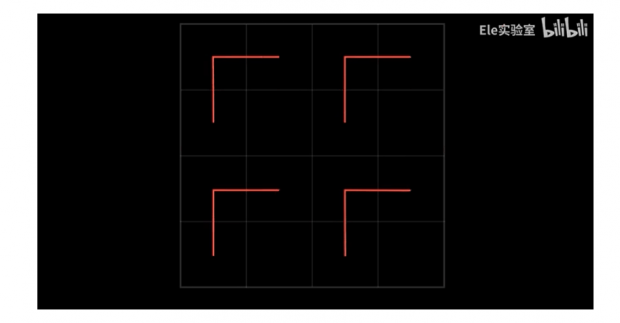
然后把下面两个分别旋转90度和-90度再把它们连起来，这就是二阶的希尔伯特曲线。
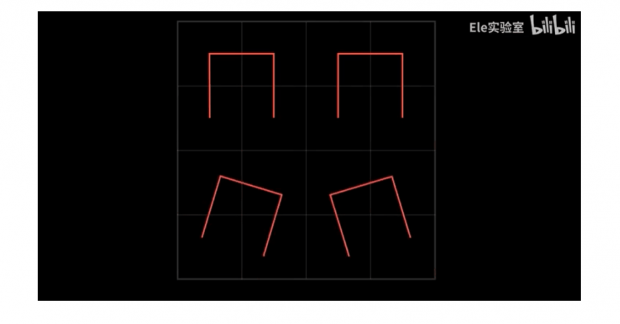
同样的道理我们可以得到三阶、四阶、五阶希尔伯特曲线等等。
而当阶数趋近于无穷的时候，我们就可以认为曲线“填满了”整个平面：
只有当这时候才是真正意义上的希尔伯特曲线，而之前阶数达不到不无穷的情况，姑且可以称作“伪希尔伯特曲线”。
通过遍历这个曲线我们就可以得到平面上所有的点，虽然希尔伯特的曲线取无穷大的时候，在数学上还有很多争议，但是对于离散系统的计算机来说，这已经很Nice了。
那么，希尔伯特曲线如何实现降维？
举个栗子：
这是一张64×64像素的，每个像素刚好是一个小方块。
我们可以用伪希尔伯特曲线穿过这些像素块，然后从线的出口处像糖葫芦一样向外拉扯这些像素，这样一来二维就变成了一维的：
当然由于我们无法做到无穷，这只是一种近似。
不过，这种降维方式的好处是希尔伯特的曲线在遍历的时候能够保证二维平面局部相邻的点在被扯成一维的时候像素点还是相邻的，从而降维后的图案就有自然过渡的效果。
三维降维打击
按照上面的原理，我们就可以开始着手对三维世界的物体进行二维打击了。
此时就要让希尔伯特的曲线的三维结构登场了，它长下面这个样子：
同理，如果用一个足够极限的三维希尔伯特的曲线去贯穿一个三维物体，就可以足够近似的遍历出三维物体的每个点：
但是就像上文所说的一样，目前主流的三维建模方式都是通过三角面去组成一个物体的空壳，即物体的内部是空的，那么这个问题该如何解决呢？
在这里Up主提出，其实除了空壳子，对应二维中像素的概念，也可以采用一个叫做“体素”的方案来建模三维物体。
体素的概念很简单，就是类似游戏《我的世界》中一个个不同颜色的基本立方块，通过不同的堆叠方式产生不同的物体，这些小立方块越小，物体的细节也就越好。
当立方块大小无限趋近于零的时候，也就达到了真实世界物体应有的样子了：
考虑到这种建模方式比较消耗计算资源，Up主在这里只采用了五阶的三维希尔伯特曲线，并产生了262,144个体素点。
另外Up主参考地球的内部构造用程序快速生成了地球的地核、地幔和地壳。
但要生成拥有大陆和海洋的复杂地表就要稍微麻烦了。
首先要读取一张地球贴图的各点像素，然后用球形贴图算法采样这些像素点映射到球面，再用体素方块堆叠成这些点。
最后我们就能得到一个由体素块构成的、同时具有外部和内部细节的三维地球。
到此，对地球的降维打击就要来了 ！
我们先来构建出一个长度和三维希尔伯特曲线一样长的二维希尔伯特曲线。
再把三维希尔伯特曲线上的各个体素方块像撸糖葫芦一样撸下来，然后再串入二维曲线，就可以达到如此降维打击的效果：
当然由于我们并不是取无限阶，所以这还只是一种直观上的近似。
最后Up主重新编排了一下把地球降维的过程，看上去更加接近“从三维向二维的跌落”。
下面就来享受三维打击的视觉盛宴吧！
简直要起飞了有没有！
网友讨论
目前这则视频在B站收获了200多万点击量，超20万点赞，不少网友直呼，好家伙，过于硬核了。
还有评论称，这才是B站知识Up主该有的样子。
就连B站知识区最为知名的百大Up主之一毕导也说强
搞笑版：
“ 歌者：我需要一张二向箔。
长老：好的，你要皮亚诺式还是希尔伯特式？
“说白了就是把一个毛线球抽成毛线”：
能不能用这种方法把三维升到四维
可以的，就像印度拿1G+2G+3G叠出了6G一样，远超中国
认真讨论版：
还有硬核的网友指出这并不是降维真正的效果：
up的这种变换是一种几何变换，没有考虑到物理因素，数学上这种变换很多。如果考虑物理因素，降维打击应该会像是物体跌落到一个平直黑洞的过程，光子本身的结构是三维的，所以，我们不能看见最终产生的2维平面。因此，我们看到的图像实际上是跌落2维前的3维状态逃逸出的光子。理论上，相当于是液压机的效果是比较合理的，取决于二向箔的吸收效率和物体的跌落速率。
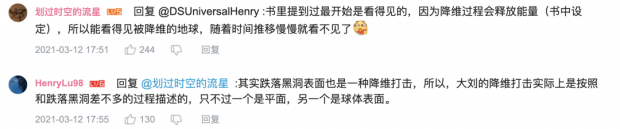
还涉及到了大家小学二年级学过的相对论效应：
按照这位硬核网友的说法，那效果难道应该是下面这样的？
目前这个项目已经在Github开源了，Up主表示，高斯帕曲线这种更加圆润的曲线效果也不错，但是voxel的堆叠方式有点麻烦，目前没有实现，有兴趣的盆友可以尝试一番。
想看视觉效果更棒的原视频，可以去B站关注一波Up主「Ele实验室」
最后，用网友的一句话来给整个事情的真相做个结尾：
“我”作为一个三维空间的生物，在二维的屏幕上看UP编写的二维模拟三维的图像进行二维降维
代码地址：https://github.com/KikiLetGo/DimReduce
视频链接：https://www.bilibili.com/video/BV1Sf4y147J9?spm_id_from=333.851.b_7265636f6d6d656e64.1
文末分享
在19年的时候市面上出版了一本《三体艺术插画集》，这里给大家放送几张精美的插画：
二向箔：
二向箔攻击：
降维打击：
罗辑与正在被二维化毁灭的太阳系：
被二维化的人：
智子：
水滴：
本文经授权转载自微信公众号“AI科技评论”，原题目为《真·降维打击！《三体》中二向箔吞噬地球的场景成真了！这位B站Up主过于硬核......》。
话题：
0
推荐
财新博客版权声明：财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有，未经博主及/或相关权利人单独授权，任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点，不代表财新网的立场和观点。
京公网安备 11010502034662号 