博客
斐波那契叶序、黄金螺旋、分形几何，植物的花叶或果实生长总是呈现某种奇妙的数学或几何结构。一直以来，人们只能从空间利用效率、生长速度、基因影响等个别因素解释原因，但7月一项对罗马花椰菜花球高度自相似的研究表明，这些有序模式是基因调控网络和形态动力学多项参数作用共同涌现的结果。这项工作登上了Science 杂志的封面。
论文题目：
Cauliflower fractal forms arise from perturbations of floral gene networks View ORCID Profile
论文地址：
https://science.sciencemag.org/content/373/6551/192?rss=1
1. 自然造化数学：从斐波那契数列到植物的叶序螺旋5. 生物数学中斑图动力学：形态发生学与基因调控网络
在植物发育整个过程中，分生组织经常以确定的螺旋形、对生或轮生模式产生不同器官。花椰菜（Cauliflowers）呈现出一种不寻常的器官排列，在广泛的尺度范围内产生许多螺旋形的嵌套。这种分形的、自相似的组织是如何从发育机制中出现的，从古至今一直难以捉摸透。最近一项结合对拟南芥花椰菜类突变体的实验分析和建模研究发现，花球自相似性产生是因为分生组织未能形成花，但保留了它们在花状态下短暂的“记忆”，并且在递减的叶间期中不断进行表达。这项研究通过建立一个SALT基因调控网络，并结合形态动力学参数，完整地解释了罗马花椰菜凝乳状、具有明显分形特征的花球，是如何从分生组织发育程序和动态定义的关键参数中涌现出来的。自然造化数学：从斐波那契数列到植物的叶序螺旋
不管植物学家是否懂得数学，但可以肯定的是，植物一定懂得数学。
例如，不同种类的花，花瓣数量是不一样的，但却并非是任意的。百合花有3个花瓣，毛莨花有5个，金鸡菊通常有8个，瓜叶菊有13个，紫菀有21个，雏菊和向日葵通常有34、55、或89个，大型向日葵往往有144个花瓣——它们都符合著名的斐波那契数列：- Fn = Fn-1+Fn-2（n>=2), F0=0, F1=1
这个规律很少有意外，如果你发现少了，那很可能是因为一个花瓣掉落了。对于叶也一样，人们常常憧憬去寻找传说中象征幸福的四叶草，也正因为这种三叶草的变异体极为稀少。包括花叶在内的植物器官，都源自一种干细胞池——茎尖分生组织 (SAMs) 的活动，由一种被称为原基（primordium）的细胞团块形成。人们很早就发现，叶在茎上的排列方式，即叶序的生长角度不是任意的，最常见的是相邻偏差角总是137.5°的整数倍，对应周期分数的3/8。此外还有1/2、1/3、2/5、3/8、5/13……其组成同样是斐波那契数列项，且比值越来越接近一个无理数——黄金分割比 ϕ=(1+√5)/2。进一步研究发现，花数、叶序和果实的螺旋线在生长过程中所接近的角度就是 1/(1+ϕ），对应圆周角大约137.507764……°的值，它也被称为黄金角度。原基在植物茎尖的生长规律如图2所示，最终各个原基呈螺旋状以黄金角度的倍数依次排开，形成了茎叶相间的奇特的几何样貌。不要小看黄金角度的精确值，只有沿137.5°生长，才会形成图3中间的费马螺线。此外哪怕有十分之一的偏差，都会形成截然不同的结果[2]。在沿费马螺线时，向日葵种子会紧密聚集在一起，中间没有缝隙或重叠。此时种子充分利用了空间，堆积效率最高。图3：偏差角度为137°、137.5°和138°向日葵形成不同的螺线不仅角度，具有螺旋叶序的植物器官，还会通常形成两个螺旋簇族（图1A-C），以正反方向转动，并出现在斐波那契数列的两个连续数字中[1]。例如雏菊（图4A）或向日葵花盘上的种子，逆时或顺时针螺旋线的数量，往往都是8、13、21 或 34条。图4：(A) 雏菊头状花序，13个蓝色顺时针和21个逆时针红色螺旋 (B) 大丽花复合花 (C) 生姜 (D-F) 花椰菜，八个逆时针（棕色）和五个顺时针（青色）的螺旋。线矩形展示了嵌套在多个尺度上的螺旋序列 (G) 罗马花椰菜花球 (H) 野生型 (WT) 拟南芥花序，及 (I) ap1 cal 变种花球。而在花椰菜中，不仅一个尺度，在多个尺度上都可以看到凝乳状的螺旋簇族（图4D-F），每个花菜的小花球就像是由一个个微型版本的花菜组成的。这种组织自相似性在罗马花椰菜（Romanesco）中达到了顶峰，其螺旋呈现类似于浮雕，在所有尺度上都是圆锥形，整个几何外观赋予了花球明显的分形特征（图4G）。维多利亚时代的科学家们信誓旦旦地认为，由于黄金分割是无理数，花叶的偏差角度或器官螺旋，让空间利用效率最高，又能避免器官之间互相遮盖，由此才能更有效地接收雨水和阳光生长。但这种简单解释，就好像未卜先知地预设了植物们生长的目的，认为植物喜欢斐波那契数列或分形是原因一样，却并没有给出「植物为什么懂数学」的形成机制。答案当然不会这么简单。最近，来自法国植物学家和数学家在 Nature上发布的一项研究《Cauliflower fractal forms arise from perturbations of floral gene networks View ORCID Profile》，对通过研究拟南芥和花椰菜花球形成机制，建立了一个基于基因调控网络 (GRN) 和形态动力学参数的模型，从分子层次解释了调控罗马花椰菜花球的形成具有明显分形数学特征的原因，对这一横跨数百年的谜题给出了一个复杂但确切的回答。构建植物发育的SALT基因调控网络
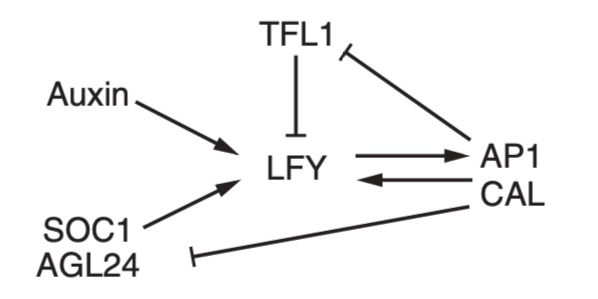
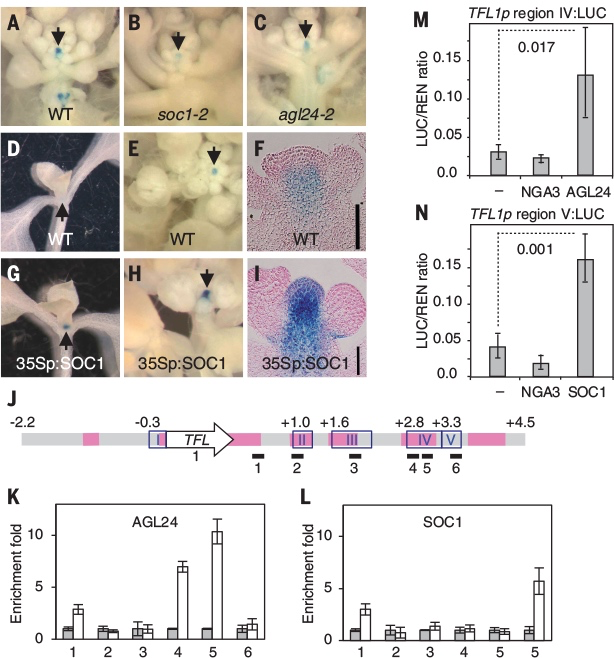
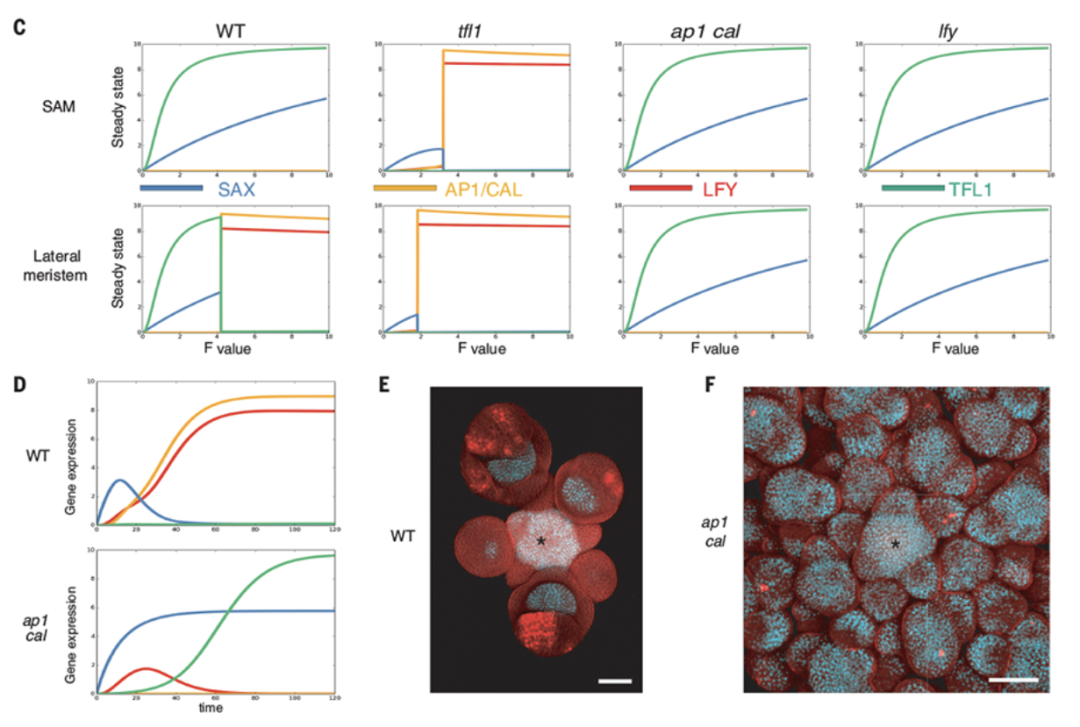
花椰菜从卷心菜驯化而来，花序呈螺旋状，每个新出现的花原基永远不会成熟到花期，因此会不断产生更多凝乳状的花球[4, 5]。这种结构由十字花科拟南芥（Arabidopsis thaliana）的基因 AP1和CAL 双突变引起（图4H-I），是编码MADS盒蛋白转录因子、促进花卉发育[8, 9]的两个旁系同源基因。控制拟南芥芽和花发育的基因调控网络 (GRN) 已被大量研究，但能否够解释 AP1 CAL 突变尚不清楚[10-16]。在拟南芥中，花的发育由 LFY 启动（图5），LFY 由 SOC1 和 AGL24 两种MADS盒蛋白，通过环境和内源性线索在整个花序分生组织中调控，并通过标记花分生组织起始位点的植物生长素最大值进行诱导，但它同时又被 TFL1 花序身份蛋白抑制。此后在花原基中，LFY 诱导 AP1 和 CAL，同时它们也对 LFY 产生正反馈，并抑制SOC1/AGL24 和 TFL1，从而确保每个新分生组织的命运是成为一朵花。但在 AP1 CAL突变体如花椰菜中，AP1/LFY 正反馈不存在，TFL1 不受产生花的分生组织中 AP1/CAL 的抑制。因此，幼花原基不能维持 LFY 表达并开始表达 TFL1。结果，它们失去了花朵身份而成为别样花序的分生组织[8]。TFL1 在新生花原基中的抑制在以往研究已理解，但直接导致它在 AP1 CAL 花序分生组织中上调的因素尚不清楚。作者通过搜索了除 LFY 之外的 TFL1 的直接正向调节因子，检查了 SOC1 和 AGL24，通过功能性丧失和获得实验表明二者均诱导 TFL1（图6A-I），染色质免疫沉淀 (ChIP) 也表明这两个转录因子会与 TFL1 区域结合，调节分生组织中的表达[22]（图6J-L）。通过在过渡相试验（transient assay）中构建 SOC1 和 AGL24，表明这些区域足以激活TFL1 并产生基因报告（图6M&N），从而证实它们是 TFL1 的直接调节器。图6：TLF1、SOC1 和 AGL24作为正向调控因子的实验研究此外因为二者的同系物 XAL2 也结合并诱导 TFL1[23]，论文将 SOC1、AGL24 和 XAL2 的活动聚合到 SAX 代理中，一起充当 TFL1 正向调节器[9]。由此创建了 SALT基因调控网络（图7），由这四个调节器、生长素Auxin [24]和代表成花激素的F值组成。后者是一种诱导花的信号，当植物老化或暴露于诱导开花的环境条件时该信号会增加[25, 26]。最后研究还在网络中添加了一个TFL1 的早期过渡抑制因子代理（eREP）。SALT网络的真实基因表达概括了在分子层次会驱动植物分生组织成为何种命运。然而，最终植物结构不仅取决于分生组织的类型，还取决于形态动力学参数，包括决定通路的分子阈值、器官生长速率、分生组织开始生成器官的延迟以及器官生产速率，这些都是独立调节的。LFY 和 ap1 cal 突变体实例说明了这一点，它们具有相同的GRN输出（图8C），但具有明显不同的结构和形态[8, 29]。因此，最终植物花序结构源于花基因调控网络 (GRN) 和形态动力学参数之间复杂的相互作用。为研究这种相互作用在拟南芥中是如何运作的，还需要结合动力学进行 3D植物计算建模。（图8 SALT GRN模型及实验验证 (A)SALT GRN网络结构 (B)SAX、AP1/CAL、LFY和TFL1在 WT 和 ap1 cal 突变体的分生组织（SAM）和侧原基中的已知表达模式。问号表示模型的预测表达模式。(C)在SAM（低生长素）和侧分生组织（高生长素）中不同F值下模型的 WT、tfl1、ap1 cal 和 lfy 稳态。预测的 WT 和所有突变体分生组织的遗传特性与实验观察到的表型一致 (D)高F值下侧原基基因表达的时间模拟 （E&F）SOC1:GFP（白色/浅蓝色信号）基因报告在WT(E)和 ap1-7 cal-1 突变体(F)中的花序表达）
形态动力学和GRN结合的多尺度生成模型
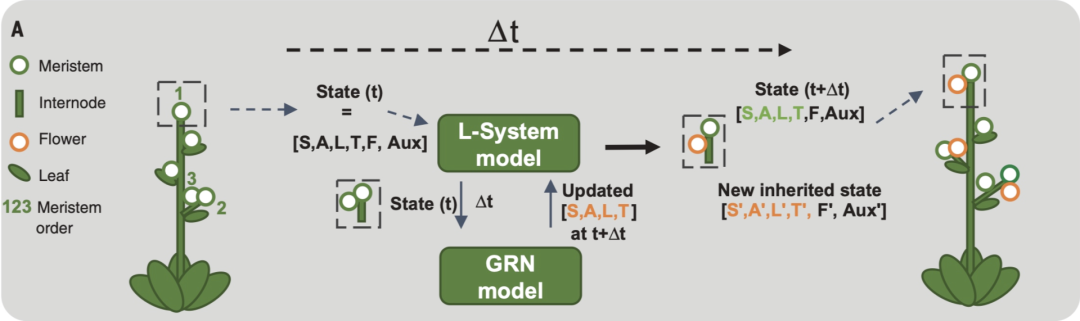
基于SALT GRN，作者将L系统（L-System）集成一个到3D计算图形模型：由塑造地面植物结构的四种器官构成：分生组织（meristems）、节间（internodes）、花朵和叶子（图9）。每个分生组织的状态标识（植株、花序和花朵）由 GRN 稳态 State(t) 决定，每个时间步的计算为分生组织先前状态和外部因素（植物生长素auxin 和 F）的函数。GRN模型实现为单室常微分方程 （见论文补充材料）。图9：拟南芥多尺度发育模型的示意图。每个分生组织状态由信号水平（生长素 auxin，F）和GRN稳态构成。在时间t，植物由一系列器官组成的（左），在时间t+Δt（右），该模型更新每个分生组织的信号水平和GRN状态。稳态定义了用于计算侧原基分生组织的标识（植株、花序或花朵）。绿色数字表示分生组织的顺序
该模型还包含描述器官生长动态的规则（节间和叶片伸长、花的生长、器官产生速度和生长初始延迟）。模拟植物从一个单一植株分生组织开始，根据GRN、形态动力学规则和F的输入值，不断重复产生新的器官。通过在合理范围内的值调整GRN和形态动力学参数，作者成功地校准了模型，产生了 WT 和 lfy 植株及 tfl1 突变体（图13B-D，movie S1&S2）的真实结构和 SAX 不开花突变体表型。但模型并没有模拟出真实的 ap1 cal 突变体，即在没有苞片或茎生叶的情况下生长出的高阶分生组织（图10a&b），这表明花椰菜表型还涉及额外的调节。图10：ap1 cal 突变花椰菜型拟南芥模拟情况作者推断，侧生的 ap1 cal 花序与其它基因型产生不同，是因为它们只在存于 LFY 的短暂表达中（图8D）。几项证据表明，LFY 的短暂表达，会抑制苞片生长[8]，也可能有助于高阶分生组织释放。随后作者通过在模型中引入一个当 LFY 超过最小阈值水平时，会上调的因子X ，抽象出了这个抑制苞片生长并释放高阶分生组织的分子路径，从而解释了侧生分生组织的递归生长。即分生组织会因花信号短暂且不可逆地通路而产生的 ap1 cal 花球结构，且不会改变 WT 原有生长动态（图13E&H，movie S3）。因此拟南芥 ap1 cal 和 lfy 具有不同结构（图8C），是因为它们花序的分生组织分子表达历史不同，从而揭示了发育滞后的存在。
罗马花椰菜花球的动态发展模型
那么这个概念框架能否解释在驯化过程中出现的可食用花椰菜 (Bob) 和罗马花椰菜变体么？
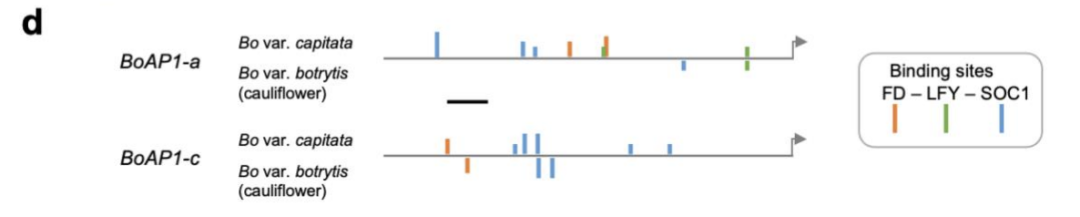
作者分析了 Bob 花球的RNA测序数据，确认了先前发现的 BobCAL 基因突变[6, 7, 9]，及两个 AP1 旁系同源基因表达水平远低于卷心菜的花序。通过比较花椰菜和卷心菜序列，确定 BoAP1 候选调节器结合位点的差异，是它们延迟激活的原因（图11）。即 BoCAL 失活和 BobAP1-a/c 表达延迟（由顺式或反式突变引起的异时性）的组合参与了Bob花球的发展。与拟南芥 ap1 cal 类似，花椰菜的最大分生组织（n≥7）比卷心菜（n=3到4）的分生组织阶数更高（图12）。尽管如此，单体大块花椰菜花球的发育却并不完全等同于拟南芥突变体[5, 7]，它还涉及形态动力学参数额外很多因素改变，例如节间伸长的减少和分支直径的增加影响。出现在罗马花椰菜螺旋所有尺度的中的圆锥形状（图1F），代表了通过驯化获得的额外几何变化，作者发现有几个形态动力学参数花椰菜发育过程中保持不变，在罗马花椰菜中却有所不同：1. 叶间期，两个连续分生组织（如叶原基）产生的时间间隔3. 侧生起始延迟。以叶间期数衡量，一个侧原基开始产生它自己的原基（或延迟侧生物）前所需的时间4. 分生组织的大小
叶序研究[37, 38]表明前三个参数与分生组织大小有关：分生组织中心区域大小的增加会相应减少叶间期，而这又反过来增加了螺旋数和侧生起始延迟。因此论文假设，在分生组织中从恒定到递减的叶间期，或许可以将花椰菜变成罗马花椰菜形态。两个分生组织平衡被扰动的证据也支持这一假设：罗马花椰菜偶尔表现出束状（图13N-O）、CLV3 的表达低于花椰菜。作者先使用了一个简化的纯几何生长模型进行测试，结果表明递减的叶间期足以产生罗马花椰菜形状（图13G），而该参数的恒定值则产生花椰菜形态（图13F）。然后在更复杂的基于GRN的拟南芥花椰菜结构模型，通过L系统中引入了相同的变化，同时保持器官生长动态在 WT 上校准。结果虽然不像纯几何模型那样规整，但花球变成了具有典型圆锥形的罗马式形态（13H-I）。花椰菜生长公示：s .PCD (t + Δt) = s.PCD(t) - cte对罗马花椰菜而言，随着分生组织年龄增长，叶间期会更快递减：s .PCD( t+ Δt) = s.PCD (t) - (cte)(s.AGE )（公式：以L系统实现递减的叶间期，L系统是生成分形的一种方法）在模拟之后进行实验验证。通过在 CLV3 基因中引入突变，直接改变分生组织的大小，对拟南芥进行实验测试这一假设。CLV3基因控制分生组织稳态并在生长过程中诱导分生组织中心区增加[29, 30]。结果如预测所料，ap1 cal拟南芥突变体中引入 CLV3 突变后，失去了球形并获得了更锥形的形状，且在不同的尺度上具有相似的结构，即罗马式花球标志特征[31]（图13L&M）。即实验观察结果也表明，分生组织大小通过控制叶间期值来调节罗马花椰菜最终花球形态。图13：原生拟南芥和花椰菜、及基因变体，在计算模拟和实验下的形态总结而言，论文建立了影响植物分生组织表达的SALT基因调控网络，并结合形态动力学建立一套植物器官形态发育的多尺度生成模型。其结果揭示了如何通过改变身份标识，影响植物动态生长和发育网络，使分生组织获得了不同的特性，并辅助调节形态发生学种种参数，最终使得自然界产生的高度多样化的植物器官和迷人的结构如分形等特征。生物数学中班图动力学：动态发生学与基因调控网络
在以往研究中，生物学家只能对生物形态发育问题博物学式地总结出规律，在环境或基因网络找到几个影响表观或调控发育的因素，或者如达西・汤普森，他在1917年的著作《生长与形式》中提出的，动物身体的形状是由不同方向和大小的生长速度造成的。然而这也只是涉及描述层面而非机制层面探讨问题。只有计算理论和人工智能的奠基人之一图灵，在1952发表的的《形态发生的化学基础》[27]中，建立了一个形态发育及斑图生成问题的形态发生学框架，在这个框架中，图灵把斑图生成的化学基础归结为初始发育系统的对称性破缺：其中作为化学物质的形态发生体，会在激活剂（Activator）和抑制剂（Inhibitor）两种形式作用下不断扩散，如果扩散抑制剂要比激活剂速度更快，就会在不同条件下就会产生不同种类形态各异的斑图。从80年代末至90 年代初，我国欧阳颀院士及其合作者在非线性动力学实验研究中首次发现二维稳态Turing 斑图，证实了Turing 理论的正确性，并有力地推动了Turing 斑图动力学的发展。在2014年，在 PNAS上发表的一篇由 Brandeis大学和 Pittsburgh大学的研究人员完成的论文《Testing Turing's theory of morphogenesis in chemical cells》[28]，通过类细胞结构，也首次为图灵的理论提供了完整实验证据，验证了他提出的模型。2018年和2020年，浙江大学张林教授和复旦大学徐凡教授又分别把图灵结构应用到了纳米尺度的化学膜结构和液体对植物叶片的生长上。此外应用图灵结构对种族入侵、扩散和捕食者系统的研究也在深入展开中[32]。尽管曾经有诸多质疑，很多生物学家认为图灵框架不能解释这么复杂的生物系统。但从近些年的种种研究来看，尤其在弥补了寻找基因调控网络的缺失后，越来越多的证据表明Turing 系统提供了描述生物系统斑图形成的总体理论框架，能够揭示从自然系统到生物系统、以及种族空间扩散的生态系统等各类系统的斑图动力演化情况。即使在基因网络研究中，例如本次对花椰菜的研究，我们也发现其实基因网络的调控也是由激活因子和抑制因子构成的，它们一起调控了植物生物发育的初始参数；因此可以说图灵斑图模型是一个跨越所有层级系统的动力学框架，如今生物学家和数学家、计算机科学家联手，再结合分子遗传学和形态发生学，才终于能对这个横跨数学、生物学、遗传学、复杂动力学系统的现象做出一个完整解释了。这是生物学家的胜利，更是伟大图灵的胜利。它不仅证明了自然、植物和各种动物懂数学，而且更说明了：唯有我们懂数学、研究数学，才能理解懂数学的生命和世间万事万物。[1] The Mathematics of Life，Ian Stewart，2011
[3] C. Godin, C. Golé, S. Douady, Development 147, dev165878 (2020).[2] C. F. Quiros, M. W. Farnham, “The genetics of Brassica oleracea,” in Genetics and Genomics of the Brassicaceae, R. Schmidt, I. Bancroft, Eds. (Springer, 2011), pp. 261–289.[3] D. V. Duclos, T. Björkman, J. Exp. Bot. 59, 421–433 (2008).[4] L. B. Smith, G. J. King, Mol. Breed. 6, 603–613 (2000).[5] N. Guo et al., BMC Biol. 19, 93 (2021).[6] J. L. Bowman, J. Alvarez, D. Weigel, E. M. Meyerowitz, D. R. Smyth, Development 119, 721–743 (1993).[7] S. A. Kempin, B. Savidge, M. F. Yanofsky, Science 267, 522–525 (1995).[8] G. Denay, H. Chahtane, G. Tichtinsky, F. Parcy, Curr. Opin. Plant Biol. 35, 15–22 (2017).[9] A. Pajoro et al., J. Exp. Bot. 65, 4731–4745 (2014).[10] B. Thomson, F. Wellmer, Curr. Top. Dev. Biol. 131, 185–210 (2019).[11] K. E. Jaeger, N. Pullen, S. Lamzin, R. J. Morris, P. A. Wigge, Plant Cell 25, 820–833 (2013).[12] C. Espinosa-Soto, P. Padilla-Longoria, E. R. Alvarez-Buylla, Plant Cell 16, 2923–2939 (2004).[13] F. Leal Valentim et al., PLOS ONE 10, e0116973 (2015).[14] P. Prusinkiewicz, Y. Erasmus, B. Lane, L. D. Harder, E. Coen, Science 316, 1452–1456 (2007).[15] K. Goslin et al., Plant Physiol. 174, 1097–1109 (2017).[16] C. Ferrándiz, Q. Gu, R. Martienssen, M. F. Yanofsky, Development 127, 725–734 (2000).[17] D. Bradley, O. Ratcliffe, C. Vincent, R. Carpenter, E. Coen, Science 275, 80–83 (1997).[18] X. Hou et al., Nat. Commun. 5, 4601 (2014).[19] S. K. Yoo et al., Plant Physiol. 139, 770–778 (2005).[20] A. Serrano-Mislata et al., Development 143, 3315–3327 (2016).[21] R. V. Pérez-Ruiz et al., Mol. Plant 8, 796–813 (2015).[22] D. Reinhardt et al., Nature 426, 255–260 (2003).[23] P. A. Wigge, Curr. Biol. 21, R374–R378 (2011).[24] J. Putterill, E. Varkonyi-Gasic, Curr. Opin. Plant Biol. 33, 77–82 (2016).[25] C. Liu et al., Dev. Cell 24, 612–622 (2013).[26] O. J. Ratcliffe et al., Development 125, 1609–1615 (1998).[27] https://royalsocietypublishing.org/doi/pdf/10.1098/rstb.1952.0012[28] https://doi.org/10.1073/pnas.1322005111[29] J. C. Fletcher, U. Brand, M. P. Running, R. Simon, E. M. Meyerowitz, Science 283, 1911–1914 (1999).[30] M. Kitagawa, D. Jackson, Annu. Rev. Plant Biol. 70, 269–291 (2019).[31] L. E. Watts, Euphytica 15, 224–228 (1966).[32] 生物数学模型斑图动力学。王玮明，蔡永丽，2020.12本文经授权转载自微信公众号“集智俱乐部”。
特 别 提 示
1. 进入『返朴』微信公众号底部菜单“精品专栏“，可查阅不同主题系列科普文章。
2. 『返朴』提供按月检索文章功能。关注公众号，回复四位数组成的年份+月份，如“1903”，可获取2019年3月的文章索引，以此类推。
长按下方图片关注「返朴」，查看更多历史文章
话题：
财新博客版权声明：财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有，未经博主及/或相关权利人单独授权，任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点，不代表财新网的立场和观点。
京公网安备 11010502034662号 