撰文 | 顾险峰

新书预告

笔者团队将过去几年中有关最优传输理论和算法的课堂讲义与研究报告加以整理总结，成书出版[1]。最优传输理论可以从多个角度去理解学习，例如线性规划和对偶的观点，凸微分几何的观点，蒙日-安培偏微分方程的观点和流体力学的观点。每种观点都发展出一套相对完备的计算方法，例如Sinkhorn类型的算法，实际上是基于线性规划加上熵正则项、或者用Nesterov方法进行光滑化，目前在深度学习领域如日中天；利用计算几何中Voronoi Diagram算法（最优传输几何变分法的C++实现）是基于凸微分几何，这种方法可以推广到球面几何情形（球面最优传输的C++实现）；将强烈非线性蒙日-安培方程用线性泊松方程来迭代逼近，并且用快速傅里叶变换来求解，实际上是基于经典的偏微分方程理论（FFT-OT:最优传输映射的快速傅里叶变换方法）；流体力学方法的物理直观最强，特别是可以将最优传输映射和黎曼几何联系起来。这本书的最后一章讲解了基于最优传输理论，从几何角度来理解深度学习，解释了模式坍塌的内在原因和新型生成模型。这本书所涉及的主要算法都配有开源代码和测试数据集合，以便于广大学生自学。新书将于2021年10月中旬开始发行，大家可以通过下面的条纹码订购：

图1：新书的网购链接。希望能够对于广大的青年学生有所帮助。我们也会进一步开源更多的相关算法。由于准备仓促，作者们的学术修养不足，书中会有不严密之处，欢迎广大读者批评指正！

 

基本问题

最近，笔者受邀给了一个公开演讲，题目为"基于最优传输的深度学习的几何理解"，基本上是新书的最后一章。这里笔者将演讲的概要记录下来，以方便听众。感谢邀请！这项工作是和丘成桐先生以及很多数学家和计算机科学家共同合作的成果。目前，深度学习在很大领域都取得了空前的成功，但是对于深度学习的理论理解依然处于较为初始的状态。我们试图回答下面的几个基本问题：

1. 深度学习究竟在学习什么？
2. 深度学习如何学习？系统究竟是学会了还只是记住了？

深度学习的学习质量如何？系统能够学会所有的知识吗？还是迫不得已要遗忘一些学习内容？

学习什么

上个世纪90年代中叶，笔者刚到哈佛大学求学，就接触了计算机视觉的两大主要流派：麻省理工AI实验室的Berthold Horn教授是视觉领域开山鼻祖Marr的同事，他主张用分析的方法处理视觉问题。在他的机器视觉课程上，他花费了很多课时详细讲解如何用双曲型偏微分方程，从单幅图像的明暗色调来计算曲面的3D几何，即所谓的shape from shading。笔者头一次看到PDE的特征线方法居然能够如此出神入化地用于3维重建，深深慨叹这一方法的优雅精巧。Horn教授的shape from shading开始用于边缘检测（edge detection）。哈佛大学的David Mumford教授是代数几何大家，他获得菲尔兹奖之后不再深耕数学，而是满腔热血地要揭示人类视觉的秘密。他受shape from shading的启发，从低维流形入手，进入了视觉领域。他提出了Mumford-Shah泛函用于图像分割，目前在医学图像领域被广泛应用。Mumford是英国贵族，在缅因海边有座古老的别墅。他在哈佛数十年，每次都把哈佛发的工资捐献回给哈佛。他也把得到的沃尔夫奖金一半捐给了以色列，一半捐给了巴勒斯坦。他是笔者生平遇到的不多的理想主义者之一，更为难得的是同时横跨数学和计算机科学两大领域。他和学生搭建了一个巨大的弧形梁结构，光源可以沿着弧形梁自由滑动，从而得到不同光照条件下Mumford人脸的照片。这样他将所有固定人脸的图像集合描述成一个三维流形：光照锥（lighting cone），自由度为光照方向加上灰度。朱松纯师兄、吴英年师兄用统计方法分析图像的纹理。他们发现Mumford提出的显式低维流形表达能力有限，无法处理复杂的纹理问题，必须要推广到高维的隐式流形。Mumford也被朱师兄的洞察和见解所折服，将研究工具从分析转向了统计。他们考虑到高维流形的复杂性，借鉴了统计物理中的吉布斯分布来隐式表达。特别是他们天才地将吉布斯分布与神经网络结合起来，提出了超越时代的理论和算法框架。当时他们提出的很多概念和方法，后来都被改头换面在深度学习中重新粉墨登场，记忆犹新的是朱师兄的吉布斯反应-扩散方程（Gibbs Reaction-Diffusion Equation）本质就是后来深度网络中的随机梯度下降方法 （Stochastic Gradient Descent）。朱师兄很多次苦口婆心地给笔者讲解他费尽心血悟出的核心思想：人类视觉中的每个“概念”对应着图像空间中的一族数据（点云），这个点云靠近某个低维流形（数据流形），并且满足特定分布，因此计算机视觉就是分析这个数据流形上的概率分布。这个思想在当时是离经叛道的非主流思想，但是Mumford和朱师兄，以及吴英年师兄都坚信这一观点。“这是一个金矿，如果你坚持挖下去必会获得巨大成功！”，很多次朱师兄都如此地劝导笔者，言辞切切，目光炯炯。数十年来，笔者内心一直都无限感激！有什么比一个年轻人在求学初始的时候，遇到一位高屋建瓴、洞悉未来的师兄更幸运的呢？时代的发展毫无疑问地验证了Mumford和朱师兄的预言！后来朱师兄在莲花山开坛授业，盛名远播，从者云集，其中就有后来名动天下的李飞飞博士。李博士从朱师兄这里求得秘笈，修炼出独门绝技ImageNet，一朝出世，横扫天下，刹那间计算机视觉的江山社稷被深度学习彻底颠覆，洪流滚滚，奔腾咆哮，摧枯拉朽，一日千里！但是，喧嚣之后，我们深知基础学术研究应该注重初始的原创性，这正是评选诺贝尔奖的最基本原则。无论如何，Mumford-朱松纯学派是最早将概率建模与随机计算引入视觉领域的人，这一历史地位当之无愧！（上面这一段回忆，因为时间限制，不会出现在演讲的正文中）根据Mumford-朱松纯学派的观点，目前也是统计学习的基本观点，每个概念都可以被视为高维背景空中某个低维数据子流形上定义的一个概率分布。这在数据科学中被称为是流形分布定则（manifold distribution law）。

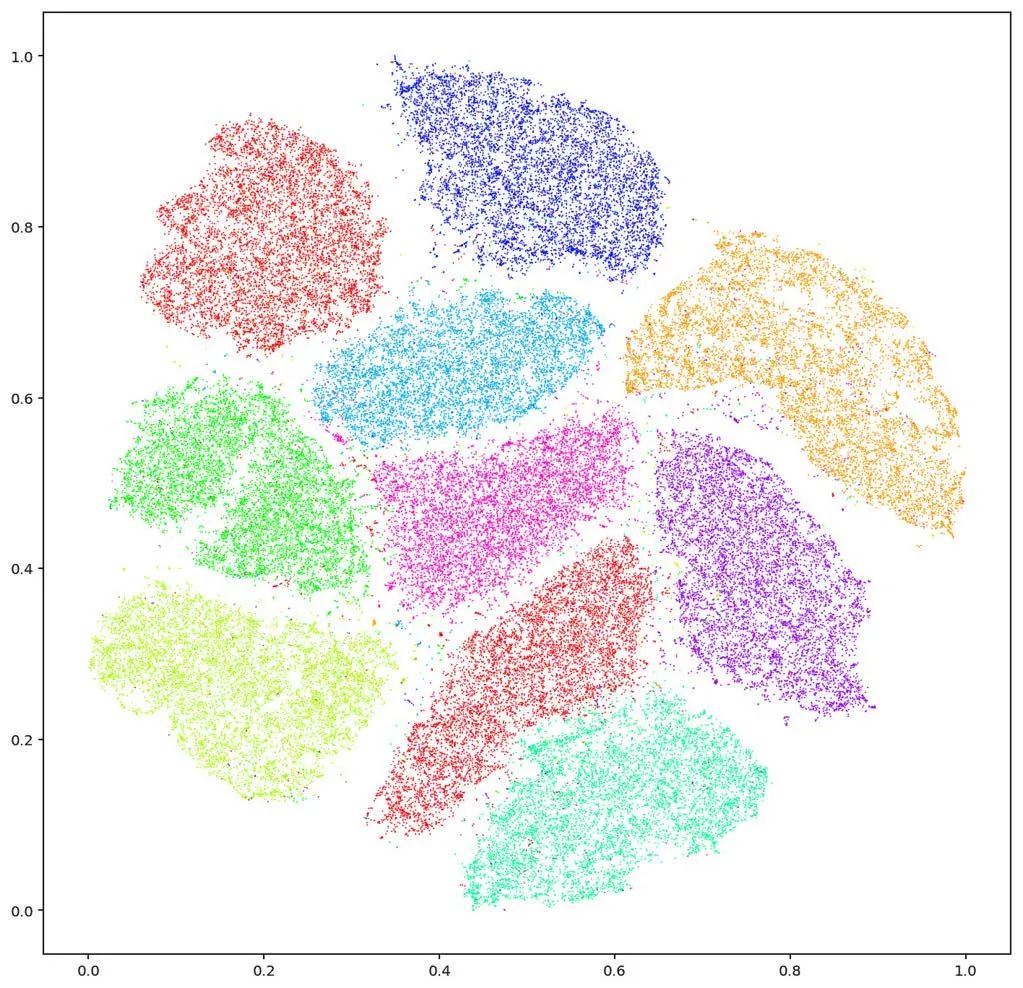
图2. 每个视觉概念是高维图像空间中某个低维数据流形上的一个概率分布。

如图2左帧所示，Yann Lecunn收集了很多信封上的手写体数字图像：每个图像是28乘28像素，可以看成是784维图像空间中的一个点；所有的手写体数字图像构成图像空间中的一个点云。那么这个点云是杂乱无章的吗？还是有内在的结构？右帧是Hinton的t-SNE算法的计算结果，将每个手写体图像（采样）映到平面（隐空间）上的一个点（特征），最为关键的是这个映射是可逆映射，即从特征我们可以得到一个采样。这意味着手写体数字图像的点云本质上是分布在一个二维曲面（数据流形）上，这个曲面嵌入在784维的欧氏空间（背景空间）之中。从数据流形到隐空间的映射被称为是编码映射，而从隐空间映回到数据流形上的映射被称为是解码映射。这个流形结构表达了数据的内禀属性，如果我们只考虑某个采样附近的切空间，则流形结构表现为切平面，局部上可以被总结为低秩特性。但是整体的流形无法用一个线性子空间来描述，用流形结构更加严谨普适。而流形的结构就是被编码映射和解码映射所表达。
更进一步，从‘0’到‘9’这十个数字被编码映射映到隐空间的十个团簇。这意味着每个数字对应一个概率分布（probability distribution），具有相应的密度函数（density）和支撑集合（support set）。由此，我们可以回答第一个问题：深度学习的目的是学习流形上的概率分布，学习任务主要有两条，一是学习流形结构（显式或者隐式地表达为编码解码映射）；二是学习概率分布（概率分布的表达有很多种方式）。

图3. 顶行：编码映射破坏了概率分布；底行，编码映射保持了概率分布。

我们用图3进行进一步解释：这里的背景空间是三维欧氏空间，流形是二维的弥勒佛曲面，分布是曲面上的均匀分布。两个编码映射都将流形映到了隐空间（平面圆盘），我们在隐空间均匀采样，再将采样点用解码映射拉回到曲面上。左上帧显示曲面上采样点的分布不再均匀；右下帧显示曲面上的分布依然均匀。这意味着下行显示的编码、解码映射保持了概率分布，实际上是深度学习的终极目标：降维（编码映射），保测度。

当时，笔者也在追随丘成桐先生学习蒙日-安培方程，主要从微分几何角度研究计算方法。笔者认为偏微分方程的分析方法更加深刻，因此并没有听从朱师兄的建议，用统计方法处理视觉问题。后来，Mumford，朱师兄，Alan Yuille等用吉布斯分布理论来表达概率分布，即在空间中定义一个能量函数，其指数函数给出了概率密度。学习的目的就是学习吉布斯分布函数。丘先生和笔者则应用最优传输理论来设计深度学习中的概率表达，而这又归结为蒙日-安培方程。这意味着分析、统计两种方法殊途同归，相互补充，相互依存。

如何学习

学习目的明确之后，下一个问题自然是深度学习系统如何学习？对于拓扑结构和概率分布的学习方法有所区别。我们这里从理论角度加以探讨。
编码、解码映射都是从流形到隐空间的连续映射。而深度神经网络具有“万有逼近”能力。这一能力可以用希尔伯特第13问题的解答来理解，即Kolmogorov-Arnold表示定理：任意多变量连续函数，都可以用单变量连续函数的复合来表示：

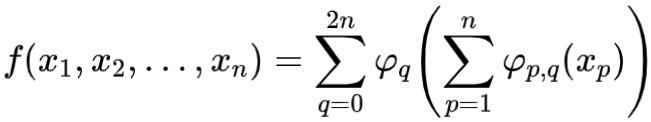
这里，每个神经元只能表达简单的函数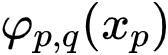，但是多个神经元复合，构成网络就可以表达非常复杂的函数。
例如，模式识别问题可以归结为这样的简单情形：拓扑空间X中给定两个闭集A与B，彼此不交，根据Urysohn引理，存在一个连续函数f:X→[0, 1], f(A)=0并且f(B)=1。因此如果神经网络能够足够好的逼近这个函数，就可以实现模式识别。对于一般的流形，由Whiteny嵌入定理，流形都可以嵌入到足够高的欧氏空间里。因此编码、解码映射都存在，学习的目的就是用神经网络来逼近编解码映射。图4显示了最为简单的自动编码器，网络中间有一层瓶颈层，对应着隐空间，瓶颈层神经元的个数等于隐空间的维数。瓶颈层左侧的网络逼近编码映射，右侧网络逼近解码映射。我们在流形上稠密采样，损失函数的设计使得编解码映射的复合等于恒同映射，这样编、解码映射互为逆映射，从原始背景空间到隐空间。

图4. 自动编码器。
图5显示了学习效果，我们在弥勒佛曲面上稠密采样，用自动编码器将曲面映入隐空间，即编码映射；然后解码映射再将隐空间映回曲面。我们对比初始数据流形与最终重建的曲面，我们看到没有太大的几何信息的丢失，所有的手指、脚趾都被展开在隐空间，即我们得到的编码解码映射都是拓扑同胚。

图5. 用自动编码器学习的流形编码、解码映射。

如图6所示，我们用的是ReLU 深度神经网络，这种网络将背景空间和隐空间都剖分成很多胞腔，每个胞腔用一个颜色来表示。在相应胞腔之间，映射是线性映射，可以用一个矩阵来表示。换言之，与传统的有限元方法相类似，都是用分片线性函数来逼近一般映射。只是有限元方法是用基函数的线性组合来逼近任意函数，而深度神经网络是用分片线性函数的复合来逼近。由此，我们可以说流形结构的学习是通过深度神经网络做万有逼近，在欧氏空间之间的所有映射组成的空间中做变分来得到。但是学习的动力学机制迄今为止没有统一的理论，学习过程是否收敛、收敛速率如何、是否收敛到全局最优，这些都有各种理论解释。

图6. 编码、解码映射是用分片线性映射来逼近的。概率分布的学习比较复杂。我们用著名的对抗生成网络来解释（GAN）。依照Goodfellow的解释，如图7所示：

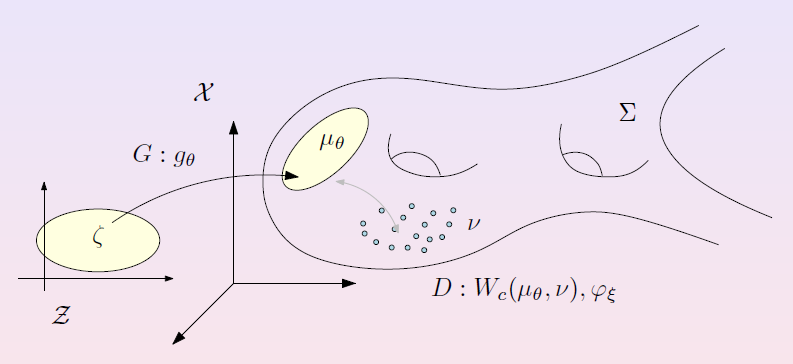
图7. GAN模型的理论解释。在隐空间上有一个已知的白噪声（例如高斯噪声），生成器将白噪声变换成数据流形上的生成分布；数据流形上的训练样本点给出了真实数据分布；判别器计算了生成分布和真实分布之间的距离。判别器和生成器彼此竞争，达到Nash均衡，人眼也无法区分生成分布与真实分布，训练终止。这里，我们看到数据分布的所有信息是由变换来表达，而两个分布之间的距离是由和之间的变换得来。因此，最终归结为两个概率分布之间的变换。而计算这些变换都是基于最优传输映射的理论和方法。

更加广泛而言，统计学习的基本算法归结为如下框架：我们希望学习某个概率分布，我们通过观察，得到这个概率分布的部分信息，表达成特定函数的期望，然后制定一个特殊的能量，在所有可能的概率分布中，优化这个能量。比如，最大熵原则就是最大化概率分布的熵（entropy）。最大似然法、后验估计，互熵等算法也类似。从理论角度而言，概率分布的学习归结为在所有分布构成的空间中做带有限制的、关于特定能量的优化。给定数据流形，上面所有的概率分布构成一个无穷维的空间，被称为是Wasserstein空间。最优传输理论为Wasserstein空间定义了一个黎曼度量，有了黎曼度量可以定义协变微分，从而使得变分法得以实行。那么用最优传输理论框架进行优化，与用信息论为理论进行的优化在经典问题上得到同样的结论（最大熵原理和最优传输）。

Wasserstein空间是无穷维的，如何定义距离、测地线、切向量和黎曼度量？换句话说，如何将统计、概率分布黎曼几何化？这是最优传输理论抽象中的抽象，可能最为直观的讲法来自流体力学。假设我们有个水池（流形），水中溶解了盐分，盐的密度并不均匀，给出了一个概率分布。我们搅动水池，让水流动起来，这样盐分会重新分配，从而得到了另外的概率分布。水池中所有可能的盐分分布构成了Wasserstein空间，给定初始分布和目标分布，我们可以设计水的定义在时空上的流场，即每一刹那，水池中的每一点处的速度向量，使得水流将初始分布变换成目标分布。在所有可能的时空流场中，存在唯一的一个使得水流的总动能（同时进行空间、时间积分）达到最小，这个最小总动能，被定义为初始和目标分布之间的Wasserstein距离。那么，这个流场在每一个时刻都有一个盐分的分布，我们得到一系列概率分布，它们构成了连接初始和目标分布之间的测地线。在每一刹那，流场可以被分解为一个无散场和一个梯度场，无散场对于密度的改变没有贡献，那么水池中的梯度场被定义为Wasserstein空间中，那一时刻对应的概率密度处的切向量。那么两个梯度场，点点计算内积再关于空间整个积分起来，如此得到了Wasserstein空间的黎曼度量。假如我们在Wasserstein空间中进行优化，我们首先关于给定能量求变分，得到水池中的一个梯度场，我们让水沿着这个梯度场持续流动一个很小的时间，然后得到新的分布，重新计算变分，得到新的流场，再次流动，直至所得的流场处处为0。

现在我们可以回答上面的问题：深度学习如何进行学习？深度学习系统在所有映射构成的空间中进行变分来学习拓扑结构，用深度神经网络来万有逼近编解码映射；在Wasserstein空间中进行优化来学习概率分布，概率分布用传输映射来表示。

学会还是记住

深度神经网络的参数非常庞大，往往是训练样本的数十倍。那么一个自然的问题在于：深度学习是否真正学会了？还是只是记住了？我们通过最优传输的几何解释来回答这个问题。

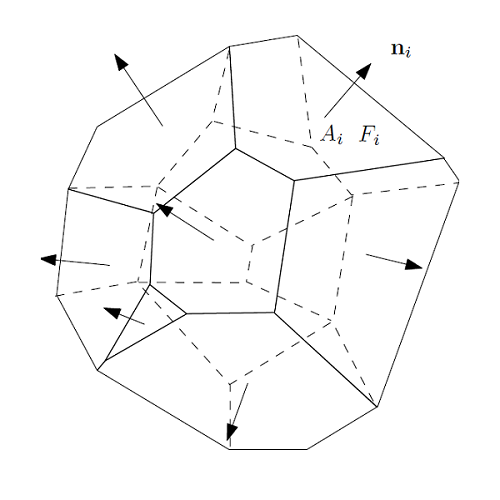
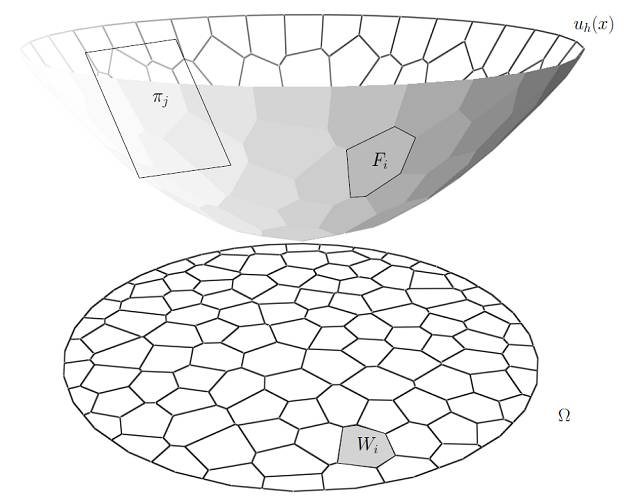
图8. Minkowski和Alexandrov问题。
最优传输和凸几何具有非常密切的亲缘关系。如图8所示，左帧是著名的Minkowski问题：给定凸多面体每个面的法向量和面积，则凸多面体的形状被确定；右帧是Alexandrov 问题：给定开放凸多面体每个面的法向量，和向平面凸集投影的面积，则凸多面体的形状被确定。而Alexandrov问题等价于欧氏平方距离下的最优传输问题。

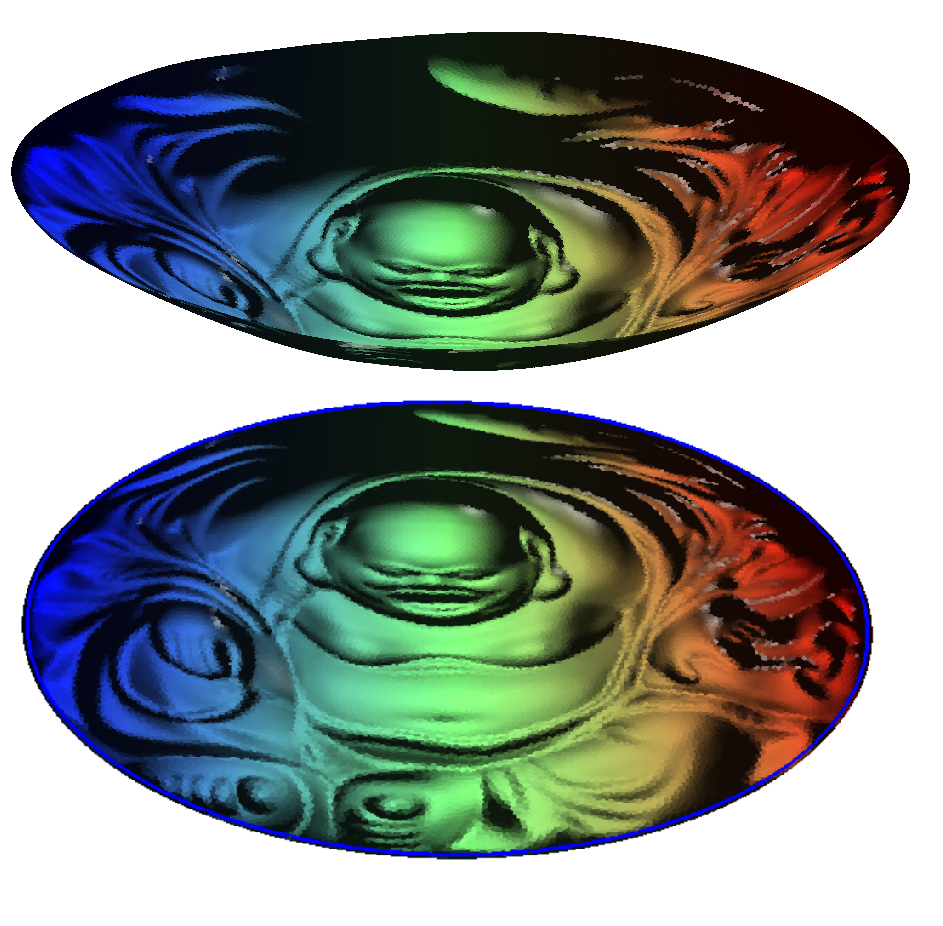
图9. Brenier势能函数。
如图9所示，根据Brenier理论，欧氏平方距离下的最优传输映射等于某个凸函数（即Brenier势能函数）的梯度映射。Brenier势能函数与Alexandrov凸多面体都是由蒙日-安培方程来控制，因此计算上彼此等价。图9显示了图3中两个分布之间的最优传输映射，和对应的Brenier势能函数，以及最优传输映射的逆映射（也是最优的），及其对应的Brenier势能函数。通过几何变分法（最优传输几何变分法的C++实现），我们可以精确计算最优传输映射，这时我们发现Brenier势能函数的表示包括了所有的训练样本，同时也包含新的计算变量。

由此，我们可以回答上面的问题：这种深度学习一方面记住了所有的训练样本，同时也学会了新的内容。

学习得如何

目前的深度学习方法不尽如人意，一个突出的问题是所谓的模式坍塌。假设我们要学习的概率分布的支集有多个连通分支，例如手写体数字有十个种类，学习之后只学会了六七个，而忘掉了其余的几种；还有一种是模式混淆，即生成的数字是几个数字的混合，而难以辨认。如图10左帧所示。
 

图10. WGAN生成的手写体数字，与AE-OT生成的手写体数字比较。
模式坍塌的问题可以用最优传输映射的正则性理论来解释。如果源和目标分布的支撑集合都是凸的，则传输映射的正则性有所保证，否则可能存在奇异点，在奇异点处映射间断。如图11所示，我们计算平面概率分布间的最优传输映射，源分布是定义在单位圆盘上的均匀分布，目标分布是定义在海马形状上的均匀分布。我们看到Brenier势能函数连续，但不是处处可导，在红色的曲线处，Brenier势能函数不可导。红色曲线投影到单位圆盘上，得到黑色的奇异点集合，最优传输映射在奇异点处间断。给定平面区域，我们可以用算法确定是否存在奇异点（深度学习的“瓶颈”与“遛狗”定理）。这样就产生了一个不可回避的本质矛盾：深度神经网络只能逼近连续映射，而传输映射有可能在奇异点处间断，这样学习过程或者不收敛，或者收敛后像集与目标并不吻合，从而造成模式坍塌。

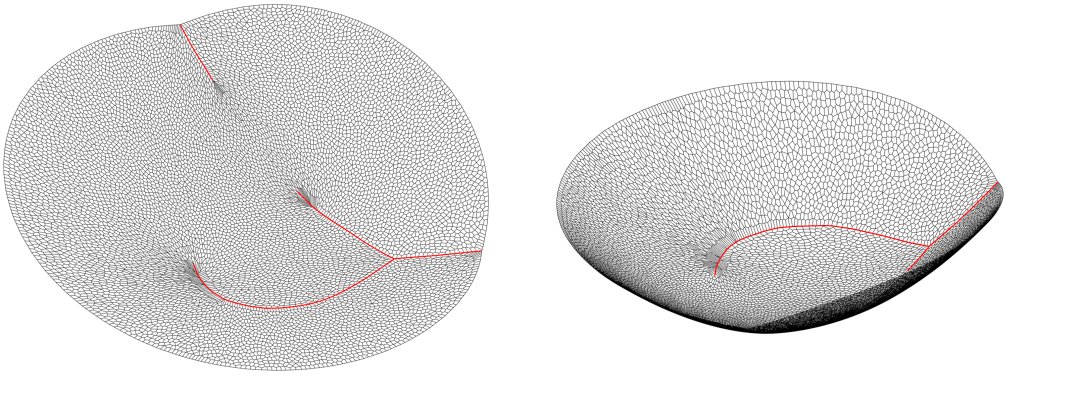
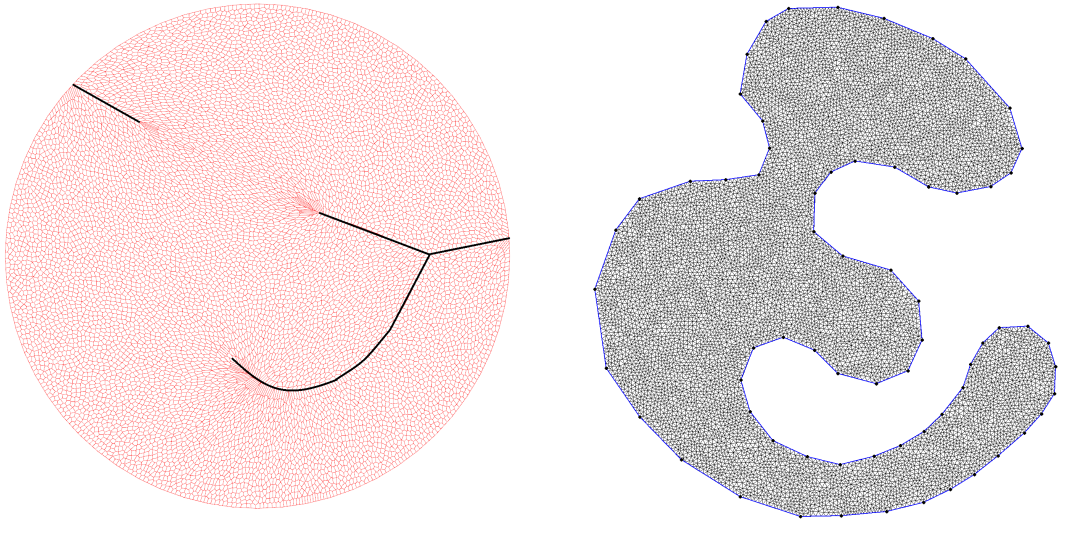
图11. 最优传输映射的奇异集合。我们可以基于最优传输理论来构造新的生成模型来避免模式坍塌。如图12所示，我们用自动编码器（Auto-encoder）来学习流形结构，用最优传输映射来学习概率分布。深度神经网络不再用来逼近传输映射，而是逼近连续的Brenier势能函数，或者用几何变分法来直接计算Brenier势能函数，这样传输映射即便是非连续的也不会影响计算精度和稳定性。

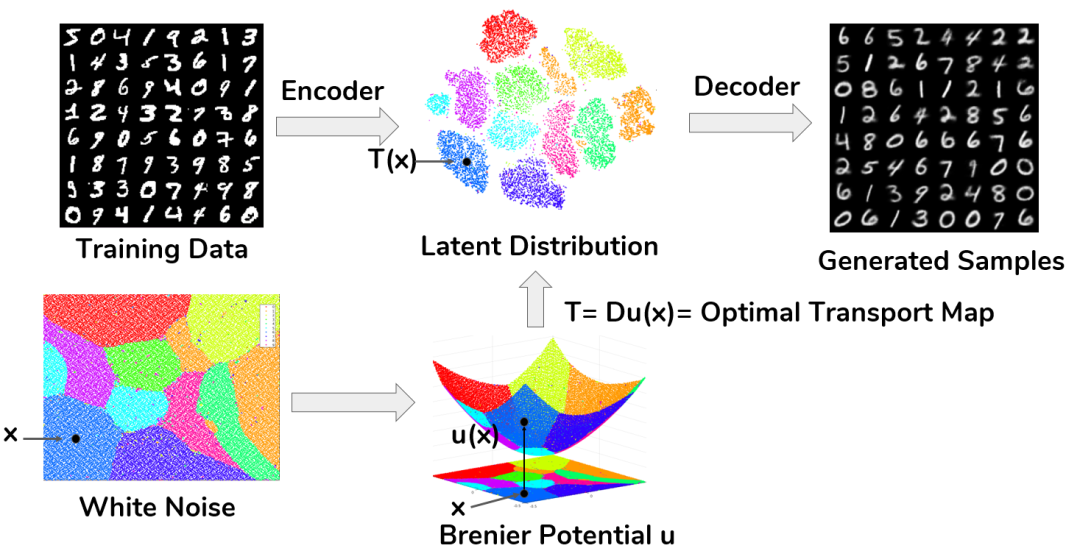
图12. AE-OT生成模型。

图13. 人脸图像流形的边缘。

这一生成模型可以精确地检测到数据流形的边缘，并且在边缘处生成新的样本。如图13所示，我们用AE-OT模型学习了一个人脸图像的流形，我们检测到流形的两处边界，一处是人脸图像带有棕黑色的眼睛，另一处是人脸图像带有蓝色的眼睛。我们在隐空间画上一条直线，映射到数据流形上的一条曲线，图13中每一幅图像是一个点，每一行是一条曲线。在曲线上出现了一只眼睛为黑色、一只眼睛为蓝色的人脸图像。这种人脸在现实生活中遇到的概率为0，实际上是人脸图像流形的边界上。学习过程非常稳定，收敛很快，没有遇到模式坍塌的问题。

小结

这里我们给出深度学习的一个几何解释：自然数据的内在模式可以表示成流形上的概率分布；深度学习的主要任务就是学习流形的结构和概率分布；流形结构学习归结为用深度神经网的万有逼近特性在映射空间中变分，概率分布学习归结为在Wasserstein空间中进行变分；最优传输理论为Wasserstein空间定义了黎曼度量，使得统计黎曼几何化；最优传输的正则性理论解释了模式坍塌，AE-OT模型可以从理论上避免，从而使得深度学习的黑箱部分透明。
演讲的详细内容请参考[2]，新书“最优传输的理论与计算”[1]可以通过扫描二维码预定。平面最优传输映射几何变分法的代码与数据从[3]可以得到，详细说明在（最优传输几何变分法的C++实现）中；球面最优传输映射几何变分法的代码与数据从[4]可以得到，详细说明在（球面最优传输映射的C++实现）中；应用快速傅里叶变换来加速求解的算法在（FFT-OT: 最优传输映射的快速傅里叶变换方法）中。

参考文献

[1] N. Lei, X. Gu, 最优传输的理论与计算，高等教育出版社，2021年10月。

[2] Na Lei, Dongsheng An, Yang Guo, Kehua Su, Shixia Liu, Zhongxuan Luo, Shing-Tung Yau and Xianfeng Gu, "Geometric Understanding of Deep Learning", Journal of Engineering, 2020. https://doi.org/10.1016/j.eng.2019.09.010[3] https://www3.cs.stonybrook.edu/~gu/software/OT/index.html[4] https://www3.cs.stonybrook.edu/~gu/software/SOT/index.html

本文经授权转载自微信公众号“老顾谈几何”。