编者按

我们即将跨入二十一世纪，在未来的新世纪中我国的数学教育必将会呈现新的面貌。然而新面貌不会自然产生，它需要我们理性的思考和积极的实践。数学教育改革中，历史的经验值得注意，有识之士的意见是宝贵的。

陈建功先生（1893—1971）是我国现代数学家和数学教育家，中国科学院院士（原学部委员）。他的《二十世纪的数学教育》一文，发表于 1952 年 2 月的《中国数学杂志》（1953 年后该杂志改名为《数学通报》）第一卷第二期，当时正是新中国成立初期百废待兴的年代。在这篇文章中，作者怀着“切望我国的数学教育有更新的革新”的殷切心情，“以中等学校的数学为核心”，对二十世纪数学教育的原则，以及数学教学内容的改革等重要问题，提出颇有见地的意见。重读陈先生的《二十世纪的数学教育》一文，对于迎接二十一世纪的数学教育十分有益。

近日文章发出后，有读者提出缺少参考文献，希望重新完善本文，于是经过编辑校对，将参考文献补足重新排版如下。

来源 | 人民教育出版社

此地所说数学教育，以中等学校的数学为核心；关于高等学校方面的数学，和小学校的算术教育，不预备在此地有所详述。本文说数学教育，以二十世纪的数学教育为主，读了下文，自然明白。“他山之石，可以攻玉”，把外国的数学教育，罗罗嗦嗦说了许多的话。笔者切望着我国的数学教育有更一进步的革新。

支配数学教育的目标、材料和方法，有三大原则：

实用性的原则

数学在日常生活中已见其有其实用价值的；如土地改革运动中的分田量地问题，关于买卖、租税、保险、奖券的计算；酒瓶的容量，箱子的体积，都是数学的应用。不但如是，数学也是物质支配和社会组织之一武器，对于自然科学、产业技术、社会科学的理解、研究和进展，都是需要数学的。假如数学没有实用，它就不应该列入于教科之中。

论理的原则

然而仅仅乎实用原则，不足以支配整个的数学教育。数学具有特殊的方法和观念，组成有系统的体系。数学并不是公式的堆垒，其所用之方法，也具有教育上的价值。

断片的推理，不但见诸任何学科，也可从日常有条理的谈话得之。但是，推理之成为说理的体系者，限于数学一科。数学具有这样的教育价值，称之为论理的价值，是为说理的原则。假如把数学当做图形集成或公式采编看待，忽视其方法和构造，那未，对于自然支配、社会组织，不但不成为一种武器，有时且成为有害的东西──例如将数学机械的乱用，导出不合理的结果。忽视数学教育论理性的原则，无异于数学教育的自杀。

心理的原则

然则上述两原则足够决定数学教育的本质么？当然还不够条件。教材的内容，对于学生宜富于兴趣；枯燥无味的东西，决不能充作教材；于是乎有心理的原则。成人所喜之推理或实用问题，未必为未成年的青年所满足。法国数学家H・庞加莱（Poincare）曾经说道：“有某教师在课室中，令学生们笔记‘圆周者，平面上于一定点等距离之点之轨迹也，’忠实的学生，记下来了；顽皮的学生，不但无兴趣去记，甚至写些别的不相干的东西。事实上，不论那一种学生，都尚未了解圆周为何物。后来，教师用粉笔作圆于黑板上，全班学生方才明白‘圆周原来是一个圆圈’。”科学家 A・爱因斯坦（Einstein）也说道：“学生仅管对于数学以外的事物，具有才能，对于数学可以朦昧无知。此种实情，其责任恐不能完全归之于学生，甚至可以完全可以归罪于教师。”吾人应该站在学生的立场；顺应学生的心理发展去教育学生，才能满足他们的真实感。某些教材，虽然具有高度的实用性价值或高度的论理性价值，假使学生不发生任何真实感，就心理的原则而言，这些教材，简值是没有教育的价值。

三原则之统一上述三原则应该综合统一而不应该对立。然则统一之关键何在? 是必须先就学生生活的环境中，使其易于接触易于理解且有实用价值的事物出发，以向论理的途径进行。所以心理性和实用性应该是论理性的向导，选择教材不应该先将实用性和论理性分别采取，然后合拢；这样勉强凑成的教材，是支离破裂的。把数学的观念和方法运用于实际应用问题时，理论上的疑问，自然油然而生；岂可以预先制成生硬的数学理论，强求适合于实用！

数学和其他的学科, 并没有什么大不相同的地方，因为他常常伴着生产力、技术发展开来的。对于古代数学的发生，恩格斯 (Engels) 曾经说过:“季节的知识老早对于农业种族或游牧民族，已经绝对需要。天文学没有数学的帮助，是无从发展起来的。所以在这‘古代 '，已经有了数学。农业发达到某阶段，因灌溉法之改进、都市之发达、航海的需要，力学跟着发生，力学没有数学的帮助，无由长足进展。”此不独在数学的诞生期为然，无论在什么时代，数学常常伴着自然科学技术、社会科学发展而发展。

数学教育家能（Nunn）说的：“数学的真理具有两面。其一面的数学真理，向时（间）空（间）的实在世界进展而与之接触。还有一面的数学真理，在数学的内部，相互对应，保持联系。数学史就是把这两面真理的不断的发展，叙述其经过情形。这两面的发展，并非互相独立，此未曾离彼，彼变未曾离此。今后的数学恐也是这样，两面不曾分道扬镳，各自存在。所以数学教育，应该使学生认清数学的发展，具有上述两重意义。数学是物质的征服和社会的组织之一武器，同时是一有秩序的论理体系。”

统一了上述三原则，以调和的精神，选择教材，决定教法，实践的过程，称之为数学教育。

01、二十世纪以前的数学教育

数学教育并不是一种幻想，乃是实践。数学教育是在经济的、社会的、政治的制约下的一种文化形式，自然具有历史性。就欧洲而言，其在奴隶社会制的古代希腊，支配阶级鄙视实践的计算术，和直觉的实践几何；重视他们所谓“和行动没有关系的真科学”──就是数论──和“抽象的”几何学，岂不是太偏重于论理性！在中世纪封建社会，教育为个人所支配，数学教育成为宗教的奴隶。事实上，此时数学教育，偏重于低级的实用性──与生产和科学脱离的宗教上的实用性。文艺复兴而后，工商业加速度的进展；生产力之发展，促成自然科学的发达，因此发生机械论的唯物论。所以十七、十八世纪的数学教育，自然强调实用性。经过法兰西大革命，巴黎成为欧洲文化的中心，因时代的要求，“一般陶冶”的话头，逐渐流行；中等教育不能专为牧师（神学）和律师（法学）的预备教育，重视所谓“一般陶冶”。其特色是将数学和近世语添入教科之中。

数学占了普遍教育的一科，是从十八世纪开始的，所以严格的说：数学教育萌芽于十八世纪。但是，数学教授的内容，大部分是“理论数学”；应用方面的数学，意识的为所排斥。究其实际，他的内容也是限于希腊时代至十七世纪间的数学；这个状态一直延长到十九世纪之末。十九世纪的数学，虽然非常进展，然而它并没有促成数学教育的改进，因此，十九世纪的数学教育，和近代的科学（十九世纪的科学），社会的生活，几乎没有关系。相反地，因入学考试的准则和其他种种考试的准则，数学难题的教授，和脱离实际的理论，成了数学教材的核心。事实上，当时所采用的几何学课本，就是欧几里得（1）几何原本最初数章；代数学和三角法，是将专门的材料，压缩而成的，太古太多，脱离实际需要。当时的物理化学等自然科学等教材，已能推陈出新；然而保守的数学，不改旧态。

到了十九世纪之末，近代科学的急速发达和各国产业的进展，经济的、社会的、思想的，给人们的生活状态以重大的变动。无产阶级的解放运动，从而开始了中等教育的内容，不能不有所更变。

02、数学教育改造的先声

保守的英国，她的几何学教本，一直沿用欧几里得的几何原本。教师们视“原本”如“圣书”，不硕苟且改变其一字一句；不但学生觉得干燥无味，教师也觉得痛苦非常；改良之声渐起，到了1870，组织了“几何学教授改良协会”（2），制定几何学要目。其结果，不过是一种微温的刷新；这也无怪其然，因为他们（协会会员）主张要不失原本精神和体裁，制定原本最初六卷的要目。他们最大的难题是“如何改造原本第五卷的比例论”──比例论是原本中最壮丽的部分。尼克宋的“改良欧几里得”（3）一书，在中国颇有流传，就是依“协会”的精神写成的几何学。

此协会到了1897 年，改名为“英国数学协会”，以 The Mathematical Gazette做他的机关杂志，登载关于教学教育的种种事情。

03、数学教育改造运动

彼利运动

数学教育改革的首创者，应该说是英国的J. 彼利（J.Perry 1850—1920）。彼利幼时做过学徒（1864—68），锻冶工场的工人（1868—70），苦学的当中，曾经旁听汤姆生的讲义（4）。彼利体验了劳动者的生活，努力于劳动者智识之增进；后来做了伦敦国际理学院力学及数学的教授，于 1901 年在英国科学协会，作启蒙的改造讲演。彼利主张的精神，是在数学的实践性，不光是说些教授的技巧。他对于数学的见解，并不是将抽象的数学理论，如何应用于自然现象或社会现象的说明；相反地，从自然现象或社会现象，由实践发见数学的法则，这是彼利所说的数学。上述彼利 1901 的讲演，在数学教育史中，是划时代的。其讲演纲要及其检讨，可以看彼利所著的书：
Discussion on the Teaching of Mathematics(Macmillan&co.1902).

彼利的意见，仍对于向来的难题“如何教授几何学？”集中，其要点如下：

（一）完全脱离欧几里得原本的形态，

（二）极度重视实验几何，

（三）强调几何的实用部分，

（四）注重立体几何，

（五）重视实用的种种测定，

（六）多用格子纸。

这次讲演的结果，自古认为经典的“原本”就因此废除。这时新型的教科书有Godfrey and Siddons,Shorter Gaomestry(1912),
Godfrey andS iddons,Elementary Algebra(1912)。

彼利在总结小组讨论会的报告，指出了下列几点全体一致的意见：

（一）几何学的实验和实测应该是证明的前提，然而也可以稍稍利用演绎法完成其说明。

（二）可采用的实验法，应由教师自己决定，随机应变，

（三）小学在算术初步，就应该使用，

（四）式子的数字计算，应该熟练；因此可使学生明了种种记号的意义，

（五）指数法则一经教懂，应该马上授以对数和对数表的用法，

（六）教材的顺序和教法应由教师灵活运用，不可呆板。

法国的学制改革

彼利的改革运动，影响及于国际数学教育。但是，法国在彼利运动以前，代数与几何，已经有融合教授的倾向，所以受彼利运动的刺激，不太利害。不但如是，法国十九世纪出版的几何书，如A．M．Legendre 的 Elements de Geome'tric（其第十二版在 1923 发行），其内容已经和“原本”大不相同，又如鲁雪（5）和康勃露色（6）合著的初等几何学（7），一直到现在，还不失为一部很好的书。但是，法国数学教育，并非毫无问题；对于考试制度的预备教育，大有使中等教育专门化的倾向。彼利讲演的第二年──1902──法国政府将中等教育制度全部革新。数学教育因此大加改良，将日常生活有关系的部分增多，又将高深的部分平易化，重视直视的几何和函数的概念。巴黎大学的数学教授 E. 波雷尔（8），依照这个趣旨，编了一套出色的教科书；算术、代数、几何、三角，都在 1903 年出版。波雷尔报告法国中学生用了波雷尔的教科书，兴味大增，成绩极优。这一套教科书有德文和日文的译本。

德国的新主义数学运动

法国1902 的学制改革和英国 1901 彼利时期的讲演，自然冲动了德国学界。德国的硕学──几何学大家──克莱茵（9）不以大学教员不与闻中等教育为然，曾于 1904 年在自然科学会议席上，作一次讲演表题“对于中学数学和中学物理的注意”。克莱茵又作成文科中学的教授要目，于 1904 至 1905 在哥廷根大学作长期的讲演，说明他的课程方案。这是德国新主义数学的原动力。德国中学教师，1905 年在梅兰（Meran）举行数学物理教授协会，作成教材要目大纲──梅兰要目。这个梅兰要目，就是以克莱茵的方案做骨子的，较诸说克莱茵原案，虽然稍为温和，然而比较过去的情形，已经出色，现在将其要点，写在下面：

（一）顺应学生心意自然的发达，排列教材，选取教材；

（二）融合数学诸分科，并且要使和其他科学有密切连系；

（三）不过于重视数学的“形式陶冶”，“应该置重心于应用方面”，养成“用数学的方法去观察自然现象和社会现象”的能力；

（四）要达到这个目的，必须以“函数观念”和“直观几何”做数学教授的骨子。

依据这个要目，就有人写成[新主义数学] 的教科书：
Behrendsen und Gotting, Lebuch der Mathematik nach Moderren Grundsatzen(Teubner,1908).
这部书（10）将平面几何学、代数学、三角法、立体几何学、微分和积分、解析几何学、近世几何学，融为一体，呵成一气，以供九年制中学之用。德国儿童，满九岁入中学，中学的种类有四，五；他的数学时数，大约每周自4 时到 6 时。

普鲁士政府指定五个中学实施梅兰要目，结果非常良好。

美国慕尔（11）的改造论

欧洲的数学教育改造运动，对于美国，没有受到强烈的刺激，其原因之一是：美国学校，老早不用欧几里得的原本，法国的几何教科书，着实通行。还有一个原因是：美国的考试制度，比较英国要宽松些，压迫不太历害，对于“考试”制度的斗争也不会激烈。但是，芝加哥大学教授慕尔，对于彼利的主张，不但拥护，并且指出美国的数学教育，大有缺点。1902 年慕尔在美国数学年会，发表他的会长讲演，题目是 [数学之基础]，他的后半段是关于数学教育的；他说：

（一）代数、几何、物理，可否不使他们一一孤立，编成“有机的统一”呢？统一而后，才能使数学物理和日常生活有密切的关系；

（二）三角法、解析几何、微积分三分科，就其起源说，又就其发展的经路说，都是和具体的现象有密切关系；所以应该把这三科的基本事项组织起来，使他们有密切关系，不应该让他们各自分立门户的；

（三）关于数学物理的教学，都应该采用实验室的方法。慕尔教授的讲演，对于美国数学教育，有极大的影响；依照（一）的精神著成的书Breslich,First—year Mathematics
Breslich,Second—year Mathematics(1906)
Breslich,Third—year Mathematics,商务印书馆老早有了译本，又Rugg and Clark,Fundamentals of high—School Mathematics一书，系1924 出版的，也是依照慕尔融合主义写成的。依（二）写成的书，也相当多，例如Young and Morgan,Elementary Mathematical Analysis(Macmillan,1917)。

总结改造运动

然则彼利，克莱茵，慕尔的数学教育改造运动的基本精神究在何处呢？基本精神是在教材教法的近代化、心理化；实行数学各科的有机统一；理论和实践的统一。结局在求数学教育基本三原则的彻底统一。详见下列诸著作：
J．Perry,Teaching of Mathematics;
Klein,Vortrageüber den mathematics chen Unterricht an denhoheren Schulen;
E. H,Moere,On the foundation of Mathematics,National Council of Teachers of Mathematics,the 4th year book.

彼利的改造论，并非狭义的卑俗的实用主义；此事已述于上文。慕尔也说：“数学教育的根本问题是如何融合理论（基本）数学和应用数学，但是不幸得很，在初等数学范围内，还保留着理论和应用的划界分疆”。改造论者主张自然科学和工程科学中所必需的“高等数学”，应该把他平易化，这似乎有点轻视数学的“形式主义”；然而这是似是而非的见解，因为数学的内容和形式，决不可以分解为二的。为什么呢？假如形式可以脱离内容而存在，这就是意味着数学是为形式而形式了。克来茵说得好；“现在吾人所宜努力的事，并不是追求两极端──形式主义和实利主义──取其一端而舍其他端，乃是融合两者成为一体”。

我们仅仅乎教授这些现实的生活上所要求的数学知识，这不能算尽了数学工作者的职，我们必须生动的指导学生，使学生们能够利用数学知识于现实问题。要使理论和实践，保持生动的关系，必须从现实自身，由实践学习得数学知识。彼利说：“教儿童推理一件事体以前，必先使他实行这件事体，儿童从测量、计算、实验，所得的结果，才能养成他的推动力。并且因此儿童沾沾自喜他的生动的创造”。这是彼利实用数学的本质。彼利著有“初等实用数学”一书：Elementary Practical Mathematics(1913),新宫恒次郎于1929 年译成日文，小仓金之助做了一篇序文，序文的未尾说道：“美国的数学教科书，号称心理的、社会的、实用的、教授法的、最进步的，但是资本主义的和事务式的美国主义的反映，到处找得出。诸君若要一本具有无产阶级实践性的强有力的数学书，我就推荐这本书。这本书可能在某些意义上是未成品，但是它期待着有光辉的未来”。彼利强调“从前的数学教材的排列，‘学者’或许认为是论理的；但是对于儿童，这些东西，完全是非论理的；儿童所能接受的论理，必须通过实验、实测、图解……。”

分科主义和融合主义

从“线”方程，“平方”方程，“立方”方程，和a 的平方，a 的立方这些用语来看，古时代数和几何未曾分离。事实上，欧几里得原本十三卷中，有三卷是算术；牛顿全集中的数学和物理融会贯通。后来许多学者，觉着数学诸分科，各有各的特殊方法，把各科纯论理的展开，颇有兴趣，方司岛说（12）把近世几何学从解析向何学分解出来，是其一例。数学不光是在学术上分了科，在数学教授上算术、代数学、几何学、三角法、解析几何学，各自陷于孤立的局面。然而在科学的研究当中，用数学做武器的时候，往往需要各科全般的知识，假如预先有了有机的统一，那就方便多了。综合的数学，不但可以避免重复，学习既省时间；并且可以使学生明白生动的数学体系。代数学中不用几何，几何学中不用代数、三角，如是严立门户，究有何益！然则统一各分科而成综合的数学，应该用什么东西做原则呢？改造论者，大都用函数的概念做统一的原则。克莱茵说：“在几何学形式的函数概念（31），是数学教育的魂魄。”又说：“以函数概念做中心，将它周围的一切数学教材，有计划的集中，就得着综合的数学。”现在把克莱茵自己作成的中学课程表的一部分，写在下面，下列三项，是德国儿童十三岁到十四岁（一年间）所应该学习的教材：

（一）直角坐标和简单函数的曲线表示──用格子纸；须注意此种曲线的全程，上坡下坡，围绕的面积等事；

（二）用函数概念做骨子，教授下列诸事项。──幂及根，一次及二次方程，圆锥曲线的初步，关于圆的计算，三角形的边角关系；

（三）多学实际之例，熟练空间的知识和数学计算。

下列三项，是中学最后一年的教材：

（一）解析的及综合的处理圆锥曲线，并且把他应用到天文学初步；

（二）中学数学全部教材的复习，用曲线或计算解决更难的实际问题；

（三）精细回顾数学全系统，并时时加以历史的说明。

国际数学教科调查会

数学教育，经彼利、克莱茵、慕尔的指导和进步的数学教师的努力，改造运动已成为国际问题。第四次举国际数学大会（14）于1908 年在罗马举行的时候，决定设置国际数学教科调查会，克莱茵等三人做常务理事，利用法国的L‘Enseignement Mathematique做机关杂志。1912 年，国际数学会在英国剑桥大学举行第五次大会，有二十七国的代表，提出各地数学教育状况报告书一百五十种，大部分已印刷发行，成为数学教育史上莫大的文献。第五次会的会长是克莱茵，克莱茵的德国报告书Abhandlungenüber den mathematischen Untersicht in Dentschland, 在150份 报告书中，最为详细。调查会的工作因战争而中止。150 份的报告书，不易卒读，叙述他的大纲的，有在 150 报告书中，最为详细。调查会的工作因战争而中止。150 份的报告书，不易卒读，叙述他的大纲的，有
Brown,Curricula in mathematics.A comparison of courses in the countries,etc.
Archilald,Training of teachers of mathematics for the secondary schools of conntries,etc.

各国数学教育的进展，因国情不同，色彩也不一致；然而改造的基调，可以说是各国完全相同。自然，改造的实际方案，不能如指导者彼利、克莱茵、慕尔所示，一一顺利进行。这是因为数学教育，以过去的“遗产”做基本；要脱离传统，成新鲜的组织，困难重重。比方说要把代数和几何融合，也不是容易的事。

04、第一次大战后的数学教育

数学教育，和其他学科的教育一样，是受社会状势的限制的。因大战而起的经济的、社会的、政治的的激动，直接或间接，对于数学教育，有莫大的影响。关于第一次大战后，各国数学教育的一般状况的参考资料，有国际数学教科调查会的报告，报告书有英文法文两种：英文的是Significant changes and trends in the teaching of mathematics through the world since 1910(数学教员会 1929 的年会)，法文的载在1929-1933 的杂志：Enseignement Mathematique.

大战中以及战后的数学教育，是混乱得很的。有些国家的教育，停滞不进；有些国家反而后退，“古气”蒸腾；有些国家，因经济的顺调进展，数学教育也得着顺利进行。先说后退的。

意大利

意国在战前，也伴着国际改造运动，有进步的倾向。其后，国家因社会的，经济的不安，酿成法西斯政治。到了1923 年，中等教育的目的和学制，有重大的变更。规定中等教育“以养成态度为目的”，作为中学教科的全部，法西斯脱所谓在文学的、哲学的、历史的立场──“国粹的”立场（15）──宣告统一了。这样一来，中等教育不必讲究实用，也不必准备做高等的研究了。教育的方针既然如是；自然科学和数学的学习和教授时数必然的削减了，

详见下表。

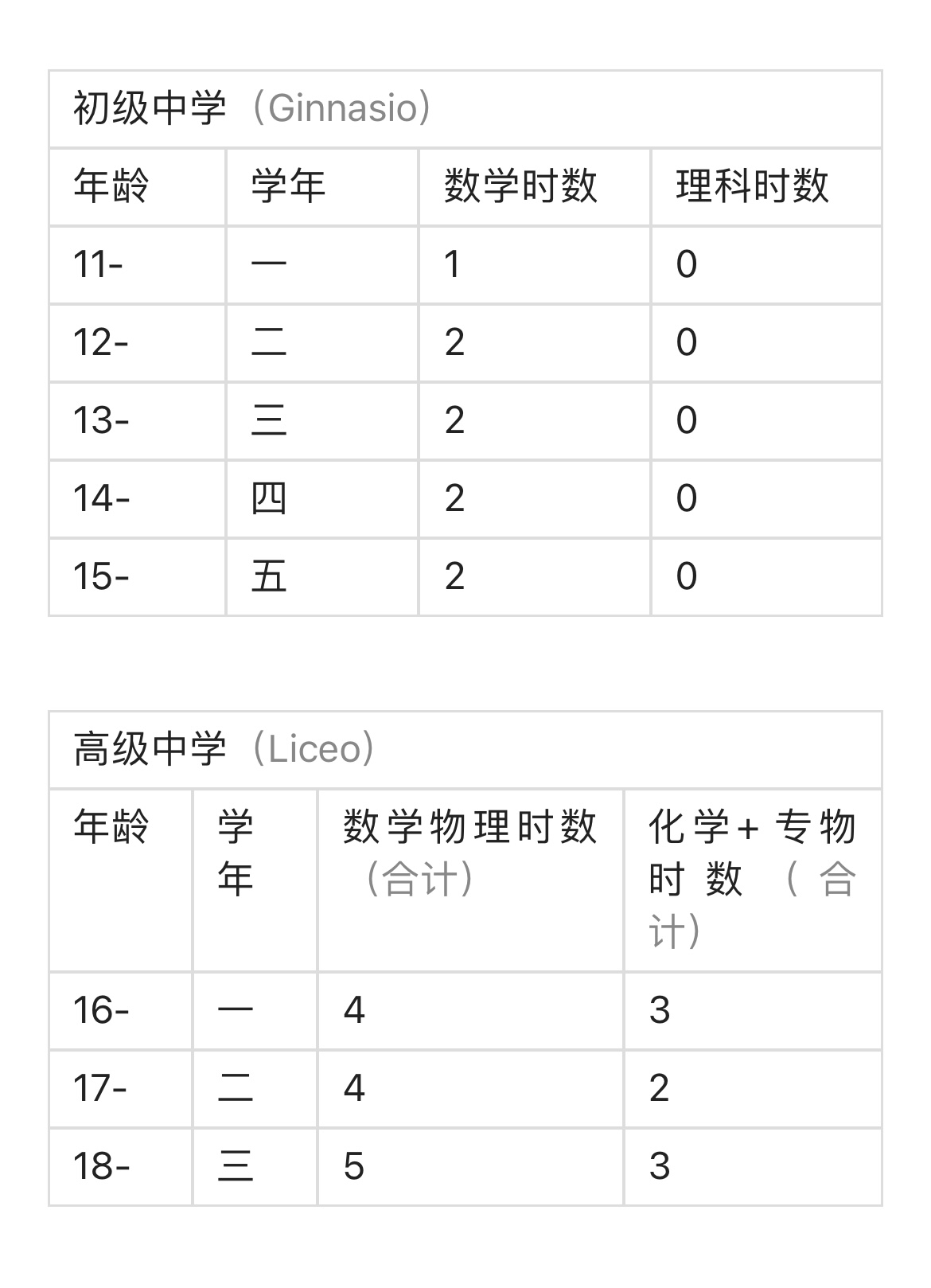
初级中学入学考试数学科目：算术，几何；
高级中学入学考试数学科目：代数，几何。

高级中学的毕业考试；数学科目是代数学、几何和三角法。此外还有高级理科中学，其毕业考试，添加直角坐标和函数与图表，大战前的教材，也有直观的、实验的、实用的部分；1923 的学制将这些东西，完全废弃，而变成形式的、抽象的、纯论理的东西了。意大利的教育部，并不公布中学校的课程要目，全部（中学毕业考试等）都是国家考试；“因国家考试的要目，有严格的规定，从页中学课程跟着考试要目也有一定的内容了。用极少的时间数，来定数学课程，只有两条路可以走：第一法：把数学程度降低。第二法：仅言纲领，把他变成骨瘦如柴的东西。意大利事实上实行了第二法。但是，以极少的时间简洁的通过数学的全程，不可能和彼利、克来茵的改造论相容。为什么？用实验实测来发现新的事实，不但需要时间、并且与”古典的精神“（16）不能一致。此时几何学家旁比阿尼（Bompiani）做教育部长，他索性把中等数学彻底变成了公理主义的数学。现在且看他的内容。某代数学教科书（7）第一卷劈头写着：

“公理 1.A=A.

公理2. 若 A=B, 则 B=A。

公理3. 若 A=B，B=C, 则 A=C。”

下文是加法的定义。然后写着：

“公理 4.A+B=B+A。”

继之以减法的定义。又写着：

“系，若A>B，B>C，则 A>C。”

这样，从抽象的、纯论理的立场出发，不容易指到事实问题了。利用方程式解决事实问题，一直到十六岁才学到，十八九岁才学到对数。第二卷供高中用，先写些一次方程，一次不等式，接着写了一章实数，用“戴德金（Dedekind）分割”导入无理数，经过复素数的定义和根数的计算，然后讲到二次方程！把  和  的存在，严密的证明了。一部代数学，供八年的用，其中应用问题，不过32 页；图表法和一次二次式的变化写成一篇附录（16 页）。到了 1932，又有一部代数学书（18）出来了，他简直把函数的变化和图表，全部除去，倒也干净。

几何书也依这个精神写成的。本来，意大利几何学教科书的着重严密性是有名的，罕与伦比的。其后因改造潮流，也稍事革新，1923 以后，又有复原的倾向。严密是好的，但是骨瘦如柴的严肃是有害的。意大利几何教科书（19），尽管最密，但是因为忽视了实验、实测、直观，不能不说是他逆转的、反动化的书。最可惊异的是：面积等事，不容许用“数计算”，光是说些几何学证明；一直到了书的未尾，才发现古色古香的比例论（欧几里得式的），把比例论和代数的无理论严密的统一了，从此才可用代数的计算应用到几何学的量上面去，但是书已快完毕了。

德意志

第一次大战后的德国，经济极度困难，要挽救这个困难，非采取产业和经济切实有效的教育方针不可。所谓作业主义，就是顺应时势的数学教育方针。作业主义，第一要学生自动去做实验实测；所以测量、画法几何、绘地圆等事，特别注重。普鲁士于1925 改革学制，仍以梅兰要目做根底，参以作业主义，教育部令说道：“利用作业，使学生获得确实的知识和明了的理解。通过作业教育期待教学的彻底……。”教育部同时又高调所谓集中主义（20），他说：“置重心于数学发达史，重视数学和其他一般文化，哲学的关系。”这样一来，对于克莱茵的“以在几何形式的函数概念统一一切数学教材”的根本思想，不能不稍事退却。依据 1925 新学制普鲁士的文科中学（21）最后四年的课程，每年都有“几何画法及测定”一科，可见作业主义的重要，他的内容如下：

第四级：作圆器具的用法，简单平面圆形。正多体体，角锥，角锥的作图。线，线分的测定，角的测定。

第三下级：点的射影，线分的射影，三角形的射影。平面的等高线及其最大倾斜线，直线的倾斜角，平面的倾斜角，两平面的交线，多角锥。

第三上级：斜角锥，倾斜体及道路的设计图，面积的测定。

第二下级：普通立体的表示，代数曲线的描写，（圆周等）近似作圆。精密度的测定，用相似论测定面积。

第二上级：圆的射影，三角法的问题的作圆，曲线的描写，测量。

第一级：关于圆锥曲线的基本问题，球的射影，天文学上的观测。

要详知其中消息，可以参阅 Scheffers und Krarner,Leitfaden der darstillenden undaümlichen Geometrie.数学教育的书有Liezmann,Methodik des Mathematischen Untersichts.杂志有Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht.

到了纳粹（Nazi）时代，状况又大变；高调所谓德国固有的数学精神，排斥“拉丁”式的和“犹太”式的数学，这方面的指导者，有柏林大学教授比巴霸赫（22）；他说：犹太人和拉丁民族喜欢纯论理的和抽象的东西，德国民族着重具体的东西。他的这些议论，多歪曲事实，比方，抽象代数学的大家多是德国人，画法几何学的创造者，是拉丁民族的蒙籍（23）。用这种见解来拥护所谓德国的“国粹”精神，根本不起作用，简直毫无意义。另一面，比巴霸赫非常推尊地老师克莱茵，说道：“在克莱茵的立场，考察日尔曼民放大的将来，实具有深长的意义。……克莱茵的改造方案，是最适应于德国民族特征的心理和性格。”到了 1934 年九月，借克莱茵的──过去的──盛名，决议了数学教育的新方针：

（一）着重实际的、具体的问题；

（二）刷新大学的数学课程，以积极的速度重视应用数学；

（三）调整应用数学教员的待遇──设置应用数学正教授；

（四）数学系学生必须学习画法几何学、力学、实用解析、或然率论。

这种政策是否光是为了发挥德国的国民性呢？只要凝视当时德国政治和经济情况，就不难知其底细。

英国

英国民族，他的自由主义和民主主义的根底相当深；或许为了这个缘故，使他的数学教育光是维持原状，进步的倾向极其缓慢。进步不速的原因很多，反对改造论革新者的存在，是一个重要的因素。对于1901 彼利的政治讲演反对最烈的，就是当时的会长（24），会长是皇家学会会员，他的话当然有相当的力量。现在将英国某中学学校的数学课程，写在下面：

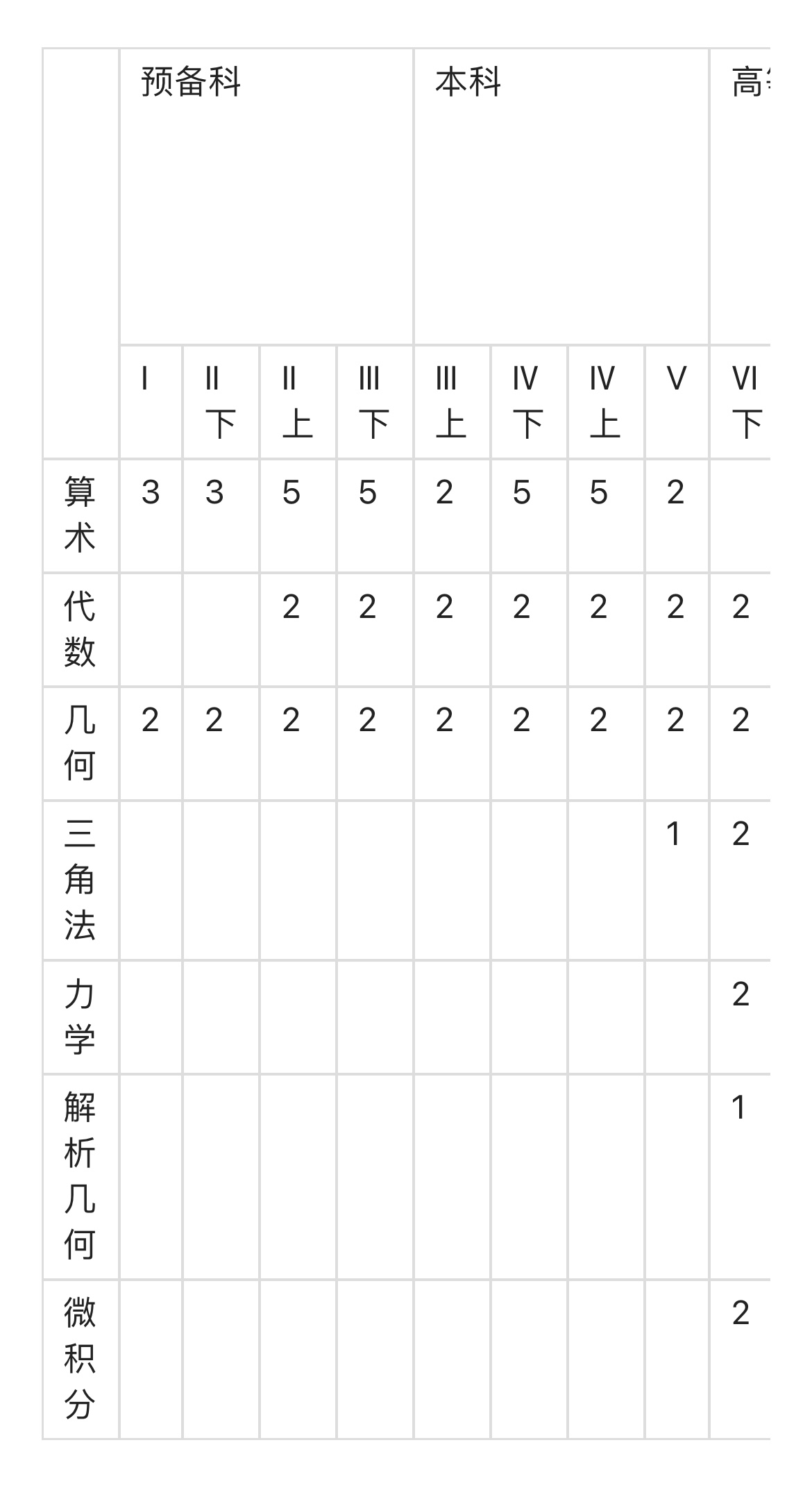
要了解英国数学教育，可阅杂志Mathematical Gazette.

法兰西

第一次大战后，法国数学教育有保守的倾向；事实上，1925 年保守内阁教育部所颁布的学制中，导入“科学平等”的原理，中学校（25）不分文科理科；其理由如下：“在现在的情况，培养‘完全人’──就是科学的教养和文学的教养保持平衡的，几何学的精神和纤细的精神的统一了的人──愈加必要了。”其结果把数学的时数，改变得像下面的式样：

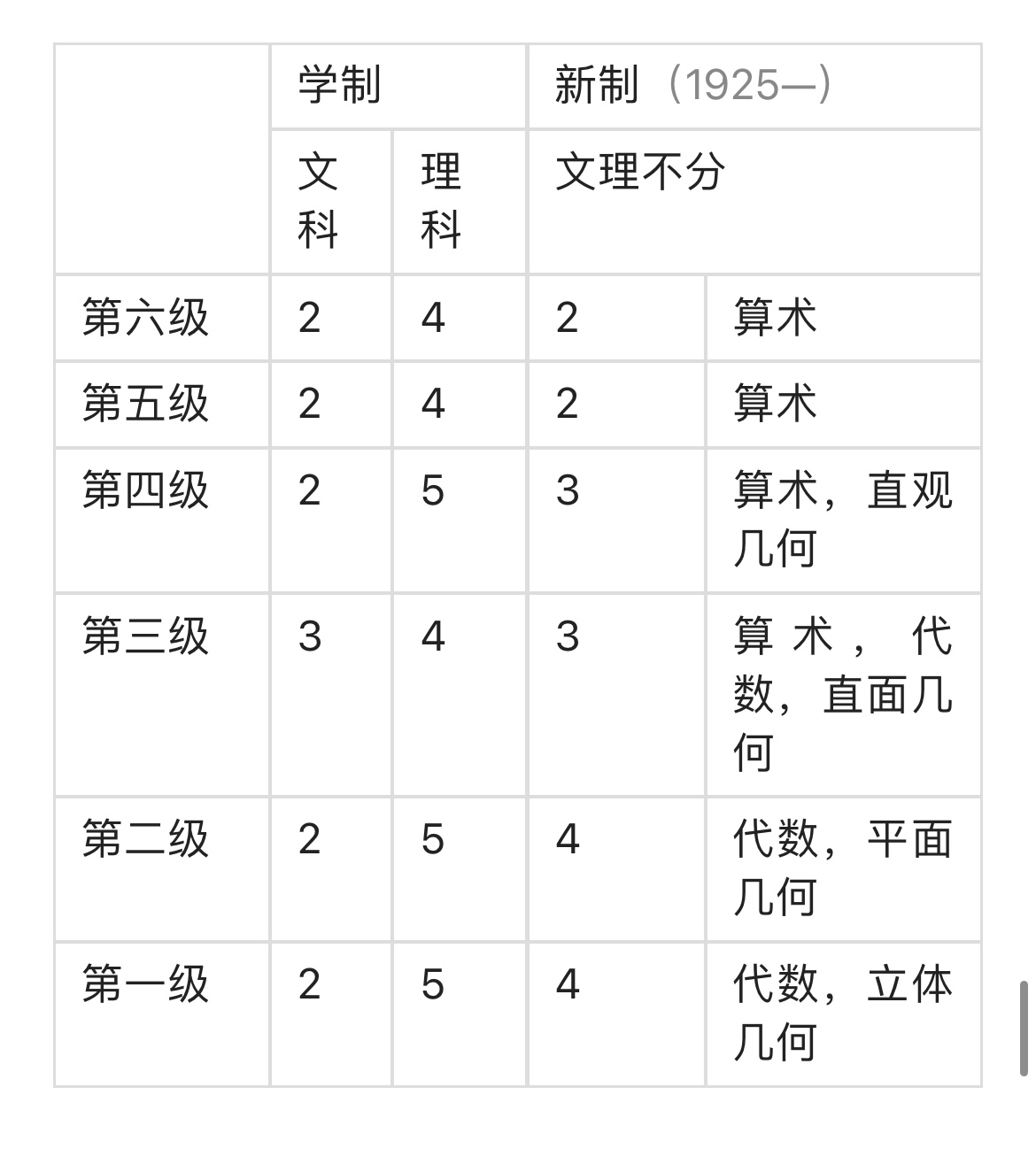
这是初等学科的课程；高等科分“哲学级”和“数学级”，前者每周教授数学两小时，课程是含有微积分的代数和天文学；数学级每周数学教授时数，课目如下：含有微积分的代数，近世几何，解析几何，三角法，画法几何。

教材要目，新制和旧制，虽然大致相同，然而精简了一些，并且将微积分移到后面去了。

要实行新学制，必须选取文理共通的教材和教法；教育部强调：“中学教育以简单明了为主，并不要求专门的知识。须置重点于精神的涵养（formation del'esprit）”

文科数学时间的增加和理科数学时间的减少，意味着实用的，科学的精神为传统的文化的精神所压迫。当时数学兼政治家潘乐卫（26）和波雷尔都公表反对的意见──反对教育部的新学制。法国中学教师向国际数学教科调查会报告说：“新学制简直没有顾到实情”。

要了解法国数学教育的实况，可阅下记的杂志：Bulletin de l'Assoriation de Professeurs de Mathematiques de l'Enscignement public.

其次，我们谈谈美国的数学教育。

美国

第一次大战，美国得着渔翁之利，经济宽裕，教育也能够向“改造的方向”进展。美国各州，教育制度并不相同，中央政府也不求其统一。1916 年，组织了一个有权威的国际“全美数学教育委员会”（27）。这个委员会，由十三名委员组织而成，其中含有数学家六名（28），教育实际家七名。1923 年二月出了第一期报告书，表题“中等教育中数学之改造”。（29）这个报告书分两部分；第一部分：一般原理及主张，第二部分：特种特殊问题的研究。其中所说的一般原理的大意如下。“吾人要有洞察和支配吾人周围的自然和社会的力量，要有以种种角度估计文化进步的力量，所以必先培养思想和行动上的习惯使有效的涵养这种力量。数学教育的第一目的是在养成分析和理解“量”和“空间”的关系的能力──对于涵养上述的力量所不可缺的能力。所以关于养成这种能力没有直接帮助的事项、方法、练习，必须排斥于课程之外。光是简化计算或玩弄计算的技巧，都是不重要的事项。用具体的事实，实际的问题抓住数的观念、方法、原理，是对于数学课程全部，是重要的，应该用力的。”然则数学教育，如何统一呢？报告书上写着：“统一数学课程最切要的事项是函数观念。……教师应将这个观念不断的放在心中，……逐步引导学生，使他们得着函数性的一般观念。”

美国中学，下级三年，上级三年（30）。数学和几何两科有不平行教授的习惯，但是委员会希望实行综合主义，制成教材配置方案教程，列表如下：

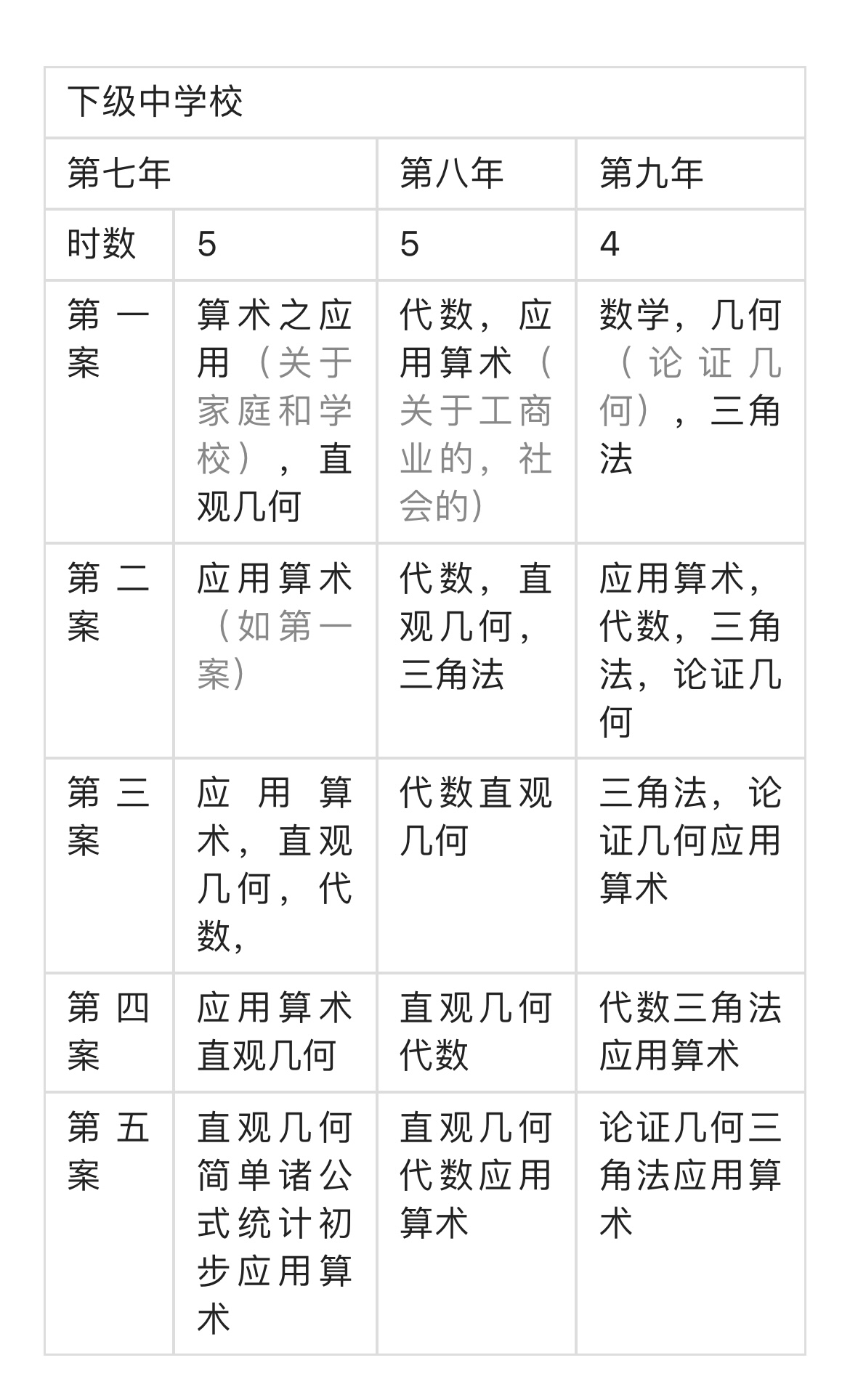
第十二年的数学，四案相同。所谓选科目，遇必要时，选择下列诸科之一：投资数学，商业数学，测量及航海术，画法几何。微积分以应用为主，不需要解析几何学形式的研究，所以表上无解析几何一科。

美国教育家关于数学教育的争论

美国的数学教育，从上文看来虽然向着改造主义进行，但是具有浓厚的实用主义色彩，且有心理化倾向。美国数学教育的心理化的原因，不能不归之于1910 年左右，关于形式陶冶的论争。什么是形式陶冶？脱离了所学习的内容而遗留下来的精神效果，称为形式陶冶。比方学习数学，不问所学过的数学内容是什么，觉得还有什么东西留下来的，这个效果是学习数学的形式陶冶。数学的形式陶冶，自古以来，一向重视；以为学习数学，可使思想精密，推理周到。但是，到了二十世纪，怀疑者出，于是发生了“形式陶冶的问题”。对于这个问题，研究者辈出，但是仍旧不能完全解决；有的否认数学教育的形式陶冶，（31）有的觉着完全否认是不对的。（32）于是乎对于数学教育的价值，也有发生疑问的。例如哥伦比亚大学教育学教授司内屯（33）竟这样说：“中学校数学，应该作为随意科，因为数学不是人人所必需的缘故”。他又说：“消费者的数学（34）──算术的一部分──自然人人所必需不可以省略，但是中学校的代数和几何，（35）未必人人所必需，不必作为正科，应改为随意科。至于数学的陶冶价值，几乎无穷小”。但是，假如数学光是有关于日常生活的部分就足够的话，那末，小学算术也嫌过多。另外一位哥伦比亚大学教授就是 D.E. 司密司，却是拥护数学教育的。他说：“教育家中，要驱逐代数学于中学校外的，大有其人；但是，这些破坏主义的煽动家根本是反动的，现在已经没有力量了”。此语见诸“司密司著，锅岛信太郎译（日文）的代数教授之进步（1925）”一书，书中又说：“二十五年前的数学教育，其目的，好像在养成数学家，现在的目的，在培养有良好教养的美国市民”。

我们于此可以断言：美国数学教育的特色，是在培养“小市民性”。美国的数学教科书，是富于小市民的实用性和学习心理的色彩。所以美国没有一本数学教科书是数学专门的人写的，著者大多是教育工作者或是心理学者。

关于这方面的参考书，有Young，Teaching of mathematics；Smith and Reeve，Teaching of junior high school mathematics；Year books of the National of Teachers of Mathematics；（1926以后，一年一册）Mathematics teacher（这是美国数学教员会的机关杂志）。此外还有The American Mathematical Monthly，是美国数学协会（36）的杂志，程度较高，不限于中学校的数学。

我国过去的教育和日本有密切关系，现在谈谈

日本

日本从明治开始，（37）事事模仿欧洲各国，不管好的歹的，一齐搬进，不十分加工，号称明治维新。明治维新的根本课题是“日本将如何追着‘先进’诸国”？为了要解决这个问题，日本政府集中力量，急速趋向资本主义。一面，日本的社会机构中，含有大量的封建残滓；经济的社会的政治的状势反映到文化和教育。日本的“移植科学”富于模仿性的缘故，自然不能够顺利进行，为民服务，时常有进退维谷的现象。数学教育当然也不在例外，一时进，一时退，成波动的现象。例如在1886（明治十九年）的学制，中学一年级有“几何学初步”一科，用直观导入几何概念，所用的书是法国式的；到了1902年，改变学制把“几何学初步”取消，几何学从中学三年级起才开始教授。所用的书是以菊池大麓著的初等几何学教科书。菊池大麓是日本最初的英国留学生，留英五年；所以他的几何学书是纯粹查式的英国式的书（当然是日本文的）。这个变更是日本数学教育的逆转，退步。1902是国际改造运动开始的时候，日本人置之不理。

1902 日本已的中学新学制；其数学要目是以菊池大麓和藤泽利喜太郎两人的意见做根底。两人都是大学教授，菊池且做过大学总长（就是校长）文部大臣（教育部长），1902 年已经封了男爵；腾泽是东京大学的有力分子（后来任贵族院议员）；日本人富于封建思想，菊池藤泽的一切意见，当然通行无阻。由是，1902 的学制对于世界大势是开倒车的；他注重分科主义，偏重论理性；他不容纳直观主义，实验和实测；不着重函数概念；将算术、代数、几何三者严格的分开，不许融合。但是，二十世纪的数学教育改造的潮流，奔腾澎湃，急速的流入日本。中学教师组成了中学数学教育会，发行杂志，研讨数学教育。政府也受到刺激，发表了种种琐碎的改造案。国家的经济，受到第一次大战的“恩惠”，宽裕得很。但是，一直到1930 为止。所得的实绩，不过是微温的改造。这是因为制造改造案的专家和实施改造案的教师都是受了旧式的──分科主义的，偏重论理的──教育，飞越起来，要他们彻底革新，他们会头痛的。

日本实行1902 的要目经过了三十年，1931 改革学制数学教育方才获得真的改造他的纲领是：

（一）容认数学各科的综合，

（二）采用直观几何，

（三）重视数值三角法，

（四）养成函数的观念。

（五）教材须适切于实际生活。

日本学制，小学六年，中学五年，高等和大学六年或七年，今将1931 的规程中的中学数学时数写在下面；

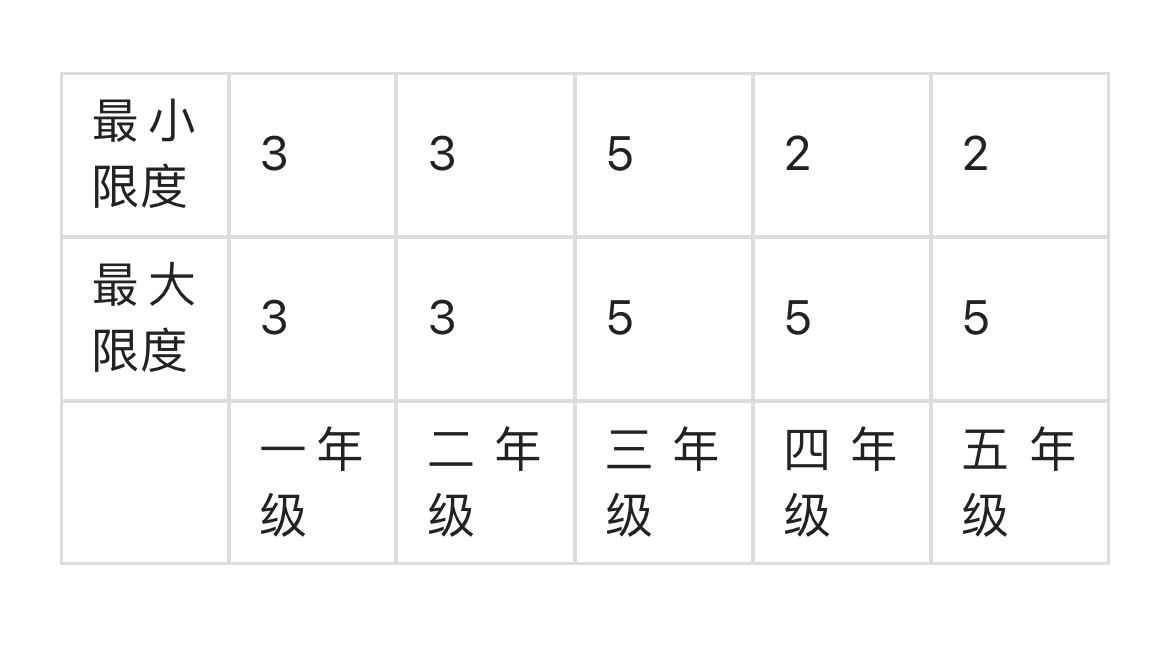
这个方案，着实进步，因为有时间的活动性使教材有伸缩的余地。但是，不进步的教师，往往要用这个时间的活动性；以为有机可乘，添入难问题，作入学考试的准备，补充旧式的教材，将整个数学还原到干燥的东西。小仓金之助于1936 四月某日利用无线电批评讲演，说道：“1931 的新规程，是极不彻底的一种似是而非的自由主义。教师可能在中学前三年，将基本教材全部告成。教育部有‘补充’一项，不明示补充的内容。教师们可能集中势力，在四五年级补充，努力于入学考试的准备，现实的学校是如此的。实际上，四五年级教科书中的问题，对于数学专门以外的人们，毫无用处，就是对于数学家自己，也是价值极低的东西。谈到入学（高等学校入学）（58）考试问题呢，大概和日常生活，自然和社会的理解，没有关系。公平立论，对于这种入学考试问题失败了的学生，仍不失为健全知识阶级的日本人；相反地，考取了的，也不过是考试所囚起来的人。中学校的上四五年级，是“入学考试职工养成所”；假如高等学校的入学考试无数学一科，数学科的存在都要发生问题了。教育部应该从速改订教授要目。……”

1945 年冬，笔者到了台湾，看到日本文部省编的一套中学数学教科书，完全采取融合主义，置重心于函数概念，面目一新，而且知道那个时候，东京方面已将算术、代数、几何、三角、解析几何，微积分呵成一气，书也出来了。但是书没有到台湾。

苏联

今年夏，笔者到北京参加课程改革会议，苏联教育专家作了很长的讲演给我们听，他说：“规定课程，改革课程是一件难事。苏联从1917 到 1939，课程屡有更变。”希望我国以苏联为鉴少走迂回的道路，苏联的普通教育制度，从 1934 学制改革以后，无大变化；至于中学，在 1939 年的党大会，才决定“于都市设立十年制的中学，于农村及民族共和国以七年制的准中学校做基础”。十年制中学设立以前，相当于中等学校的，有“单一劳动学校的第二科”。这种学校的目的，一面是普通教育的继续；一面是完成普通教育，建设唯物论世界观的充分坚固的基础。因此，重视

（1）社会科学，（2）实际的自然科学。

事实上，课程中的数学、物理、化学、博物时间数的合超过总时间数的三分之一。其中数学时数，分配如下：

其第五年（其实是初年级）的教授要目，摘出数项于下：

（一）十进法，整数和小数的计算，百分率。简单的方程式。

（二）直线，线分，测定，米达法，经验事实的图表。测定误差的估计，近似计算。

（三）分数，素数，最小公倍数，分数和小数的计算。

（四）直角及其等分，圆及其应用（图案上的）。平等四边形，多角形的面积。

（五）指数，平方根及其几何学的意义，立方体等体积公式，三角锥的表面积和体积。

（六）比和比例。

（七）一元一次方程（数字系数）：之实测，圆周公式，圆面积公式，圆锥的面积和体积，三角形（已知三边）的作图。

（八）测地作业。

光是看了这个摘要，可以知道他是倾向于改造论的。再细察他的第九年的教授要目，“更可以明了他的精神所在”。

（一）等差级数及等比级数，应用问题。

（二）变数法，无限大，无限小，极限，极限的基本定理。无限等比级数。

（三）用两有理数列定义无理数，及其相关联的基本事项。

（四）正多角形，圆周及圆面积，曲面体的体积（加乏利害原理的应用）。

（五）三角法。

（六）高次方程式。

（七）排列，组合，二项式定理。

大致和德国的教授方案相类似，但是第九年的（三）这一项，的确是特色。但是苏联十月革命后十余年间的数学教育方针，和彼利及克莱茵的思想，未必一致。上述教授要目的说明：“数学在教育上的地位，可以简单的规定如下：数学对于学生，是实际上必要的学科。在学校；在后来的生活──不管什么职业──有他的必要性的缘故，是一个不可不与之相观的工具”。因功利上的目的，实际的必要，而承认数学在教科中的地位。但是高利曼（39）不以为然，说道：“这样，自然把数学开倒车一直达到阿尔基米特斯；但是，这些努力，和辩证法的唯物论，没有任何共通点”。用同样的意义，摩洛铎西（40）对于数学研究的全般下了批判（1933）：“人们往往这样主张，数学的发展，其目的在满足今日社会主义建设的需要；将可以满足这个要求的数学诸分科发展起来就好了。但是这种主张是不对的，当然，计划数学的发展，必须把实践需要的满足和社会主义建设的展望放在心上。

但是要进到这个目的，仅仅乎将若干的分科片面的发展，是要失败的，一定要把‘全数学’计划的发展，然后可能。”

十年制的中学教科书，1949 发行的，吉西略夫（41）著的，已经由东北人民政府译成中文。

中国

二十世纪初叶，中国才订了学制；学制是“削足适履”式的日本制度。中学的数学课程，形式上和日本的无大差别。教科书也有许多译自日本的──（42）比方前述菊池的几何学。（43）国际改造潮流一时冲不进日本，中国更不消说，一直到解放前夕，旧式的数学教育，未曾动摇。中途摹仿美国；美国的教科书，盛行起来了。有些学校简直用英文原本，中学教科书用外国文，当然是限于殖民地或半殖民地的，且所用的原本，往往在其本国已经早停止使用──例如“范氏大代数”。因此，数学教育，不但成绩不良，且其目的也不明了。学生视数学如仇敌，成了中等教育上一个大问题。

解放以后，中央教育部成立不久，就召开全国教育工作者会义；1950 年，又召开精简座谈会，大家同意这样的原则（包括数，理，化）：

（甲）精简的目的在求教学切实有效，而不是降低学生程度；

（乙）删除不必要的或重复的教材，但仍须保持各科科学的系统性完整性；

（丙）六三三制，暂不更变。

关于数学教材的精简原则是：

（一）要与实际结合。要与理化学习结合，要与经济建设的科学知识结合。

（二）太抽象的材料宜精简或删。

（三）数学课程仍规定为算术、代数、……解析几何。

这是创举，值得庆祝的，但是，笔者愚见，还有几句话要补充。（乙）项的保持各科的完整性、系统性，是含有分科主义的精神。国际中等教科改造的倾向，不但融合数学的各分科，并且要融合物理、化学、博物诸科。事实上，日本在第二次战争结束前，已将中学的理化博物融合成一科了──理科。编著教科书，是由于集合许多专家，会议作成的。苏联的教科书，虽然还没有整个的融合，但是日新月异，向融合的方向进行。总而言之，（乙）项的第二段，规定的太呆板了。失去了进步的倾向。同样，数学的第（三）项的规定，应该是暂时性的。吉西略夫的高中代数学中，函数与图表，着重得很，这不是代数学和解析几何的融合么？不过以代数为主体就是了。又关于第（一）项，细察精简纲要（草案），看不出什么地方有（一）的精神，例如初中几何、高中立体几何、高中代数、高中平面三角法、高中解析几何诸科的精简纲要，不过将美国的几本书──三S 几何、范氏代数、葛氏三角、三氏解析几何──简化了一下。要他具有（一）的精神，是不可能的。话说回来；这是数学教育具有生气的开端，当然是温和的，不能希望他有太多的结果。

05、总结和展望

处这个大时代，要过有意义的生活，做有意义的工作，必先具有理解自然和洞察社会的能力。所以必须养成对于这种能力有效果的“思想和行动的习惯”，这就是教育。数学教育呢？学了数学，要使能够分析和理解这种思想和行动的习惯上所不可缺的“数量与空间的关系”。不但如是，理解和分析数量与空间的关系，也是数学的特征，所以是数学特有的任务。数学教育的目标既然在此，数学教科首先要综合和统一下列（甲），（乙）两方面：

（甲）数学是物质支配及社会组织的一种手段；

（乙）数学具有特殊的观念和方法。

然后用教育的技术，指道学生学习数学，就是说：

（丙）顺应学生的心理，分配教材，指导学生学习。但是，我国过去的数学教育呢？第一：教材全部是陈述的──十八世纪以前的，把近代数学，置之度外，以（乙）来看，是太古了。第二：内容太偏重论理性，忽视学生的心理过程；是不合于（丙）。第三：对于理解近代科学和社会生活，太少力量；这是没有硕到（甲）。无怪乎中学生的90% 以上，认为数学是干燥无味的，最不容易学习的。这种教育，当然是不会有成绩的。

到了今日，上述种种缺点，还未能十分清算。特别，上面所示的数字90% 仍未能减少，恐怕光是以“简化为精简”的改造政策，不能解决这个问题。“草案”根本没有硕到“精”的一字，“简化”也似乎缺乏原则性，然则应该如何精简？

（一）代数计算，是一种极便利的机械的技术。但是中等教育决无人人都做成代数计算熟练工人的要求，所以一切繁难的，非实质的计算；缺少真实性的问题都应该除去。三角法也应该如此处理。

（二）学习几何，应该从直观几何入门，大概是没有疑问的。然则如何处理论证几何学呢？几何学具有完整的体系，是论理的组成的，他有其他学科所不能及的美观和价值。但是，全部几何学教科书，往往充满着定理，命题，难题等等；除了少数的学生而外，大多数学生不能愉快接受。这是应该简化，应该想出办法来简化。笔者以为假如将公理的条数适宜的增多，一定可以免除冗长的毛病；将有些定理（普通教科书中的定理）改为公理，学者自负的专门家（几何学）未必以为然，但是教育上是有意义的，有好处的。假如又把普通几何教科书中的难题全部除去，学生学习的困难，一定可以减少。这样的简化，对于几何教育的目的，仍未有所损失；因为简化了几何学，不但仍保留着论理的精神，并且空间的基本事实，仍得一一了解之故。几何学全体的结构，既然已能理解，这方面的教育目的，不能不说是已经达到。对于有志深造的学生，要明白几何学的完全论理系统的时候，有了这个基础，也是事半功倍的。

由于（一）和（二）的两原则，将教材简化，中学数学一定可以减少 20% 到30%。然则用什么东西补充呢？

（三）微分积分的概念，是可以平易的直观的说明的（44）。中学生应该使他们理解速度与加速度的关系，二次函数的变化率，（简单）曲线形的面积的求法等等，从这些事项，微分和积分的概念，可以油然而生。添加了一点微积分的概念和计算法，便可应用到近代自然科学上去，使数学和产业技术有密切连系。

（四）添加社会经济方面的数学，使学生对于社会认识有帮助。例如统计法的一般──统计的量的平均、标准偏差、歪度、相关系数、由实验结果作成的实验式──就是这种材料。精简原则的“草案”，没有一个核心，未免散漫。

（五）数学教育的核心，在乎养成函数观念。所谓函数观念，其义甚广，并非专指函数的解析表示，或函数的图表。比方。绍兴距杭州50 公里；上午七时，陈某从杭州出发向绍兴，赵某从绍兴出发向杭州；陈某每小时行六公里，赵某五公里，要问两人何时何地相逢？对于此问题，研讨两人在瞬间的地位，以求位置和时间的关系，这就是函数的观念。有人看了吉西略夫的初中代数学，因为书中没有函数和图表，就以为他并不用函数观念来写书；这是近视的看法，将函数观念的意义呆板化了的缘故。即使没有任何计算，假如能够理解量与量之间的关系，对于实际生活就有用处。又假如脱离了函数观念，学习了形式的代数，完整系统的形式几何，生活上有什么意义呢？固执的人们，硬说函数观念是属于高等数学的，至少初中数学里面可以没有，但是函数观念和吾人日常生活是不分离的。以函数观念做数学教育的核心，就是要数学和人生保持密切的连系。

（六）教授数学史，不但可以提高学生学习数学的兴趣，并且数学史料，也是数学一部分，学生应该知道他的大意的。关于中国的部分，尤可以增高爱国的情结。但数学史科，不宜以中国的为限。比方吉西略夫的初中代数，在第二章的未尾，说道：“在中古时代，印度数学家（45）才提出了正负数……的计算法则（620 年）。………但在欧洲大陆上，直到 1544 年，负数的意义，还不能完全领悟。………”云云。可见吉西略夫所采的史料，并不限于苏联。数学史既是数学的一部分，宜随处插入，不必设专科。用（一）和（二）的办法简化；（三），（四），（五），（六）的办法去加精，这是笔者对精简原则的个人见解。

参考文献

(1)Euclid的几何原本共一十三卷，明徐光启有译本。其最初六章是平面部分。(2)The Association for the Improvement of Geometrical Teaching.
(3)R.C.J. Nixon, Euclid Revised(Oxford, 1876).
(4)参见Proceedings of the Royal Society of London, A III(1926).
(5)E. Rouche(1832-1910).
(6)C. Comberousse.
(7)此书小仓金之助译为日文，且加以注解和附录。
(8)E. Borel(1871-1956)长于函数论和或然率论，法国众议院议员，做海军部长。
(9)F. Klein(1849-1925)，是数学家，也是一位数学教育家，哥廷根大学教授。
(10)这部「新主义数学」森外三郎受日本文部省(教育部)的委托，译成日文，于1914成书，1916印行。
(11)E.H. Moore(1862-1932)，从1897到1902任美国会会长，是一位有名的数学家。
(12)Karl G.C. von Starrdt(1798-1867)，德国人，初做中学教师，后成有名的几何学家。
(13)Funktionsbegriff in Geometrischer Form.
(14)The International Congress of Mathematics, 大会每四年一次。因战争的缘故，1943的会移到1950在匈牙利举行，中国出席的代表有华罗庚。
(15)此地所谓文学, 是罗马意大利的文学。
(16)意大利的学者恩利格斯(Enriqnes)说:“现今意大利的教育方针, 和古典主义教育精神相一致。”
(17)Baroniet Conti, Algebra, I,II(1924). 第一卷供初中用，凡160余页，第二卷供高中用，凡220余页。
(18)Bettini et Ciamberlini, Algebra(1932).
(19)例如Bettini et Ciamberlini, Geometria(1932).
(20)Konzentration.
(21)Gymnasium.
(22)L. Bieberbach.
(23)G. Monge(1746-1818)，因筑城设计，需要繁杂的算术计算，蒙日发明画法几何，可以避免计算。
(24)会长名A. R. Forsyth(F.R.S.)，他说:" It seems purely impossible."
(25)Lycee.
(26)参见杂志, Enseignemeut mathematique(1933)和Organiser(1925)。潘乐卫(Painleve)，曾任法国内阁总理，1919来中国，时徐世昌做大总统，北京大学授潘乐卫以名誉学位。
(27)The National Committee on Mathematical Requirements.
(28)数学家有E. H. 慕尔和D. E. 斯密斯(Smith, 哥伦比亚大学教授)。
(29)The reorganization of Mathematics in Secondary Education.
(30)Junior high school, Senior high school.
(31)例如J. Dewey, E.L. Thorndike等。
(32)例如前述报告书第二部分中“形式陶冶的现状”一文(Blair著)。
(33)Snedden, Educational psychology.
(34)Consumer's mathematics.
(35)1920夏，陶知行在杭州第一师范学校，讲演新教育，也有这种论调。
(36)The Mathematical Association of America，1914年组织成立。
(37)明治元年即1868；其在中国适曾国藩为大学士兼直隶总督。
(38)高等学校三年(有的是两年)毕业，其最后一年，程度大致相当于我国大学一年级。
(39)З. Кольман. 永田广志译，马克思主义哲学的现阶段。
(40) В. Н. Молодоший.
(41)A. П. Киселёв.
(42)也有几册是美国书的译本。
(43)商务印书馆有译本。
(44)从前日本中等工业学校的微积分，就是取了这种体裁而得成效的。美，英，德，法的中学也是如此。有此等先例可援，(三)决非笔者的空想。参见前述德国新主义数学，法国波雷尔代数学。
(45)Brahmagnpta(598-?)。