整理 | 叶凌远

Never ever calculate unless you know the answer.（ 如果你不知道答案，不要马上开始计算。）

我们听到的时候当然非常震惊。经过高中的教育，我们那时都认为物理全部的意义就在于尽可能多地计算。Rudolf Peierls 也曾对年轻的 Hans Bethe 讲过：

First think, then do the integral. （先思考，再积分。）

下面这段著名的话引用自凝聚态物理学家Sam Edwards：

Keep throwing out the inessential until the problem becomes trivial. Then go back one step. （面对问题，先排除掉一切非本质的因素，使得问题变得简单。再回过头看，如何补充丢失的琐碎。）

在我自己的教学经验里，大多数学生都希望将一个问题弄得越复杂越好，而不是尽可能找到其本质，将其变得简洁。然而，上面这些话都是说起来容易，做起来难。因为我们都知道，思考远比计算要难得多。

当我刚到UCSB（加州大学圣芭芭拉分校）的研究所时，我主持的讨论班要求报告人不能在黑板上写超过十个公式。有一些人完全无法达到这一要求，因为他们经受的训练只教会了他们如何书写大量的公式。这让我想到，当我对 Weinberg 说我想写一本有关量子场论的教材时，他告诉我，要先写一本有关物理的科普书。市面上有很多很差的教材，因为许多物理学家不知道如何对物理内容进行阐释。只有能不用公式向大众传递物理的思想之后，你才能真正用公式把物理教给学生。

我相信，包括我在内的许多教授都观察到的一个现象是，有许多在课堂上表现得很好的学生，他们能在考试时表现得很好，得到很不错的成绩，但最终他们的研究并不出色。这是因为，作业和考试与做研究大为不同：面对前者，我们已经知道某个正确答案必然存在，且大多数情况下，只需要运用课堂内学过的方法就能解决这些问题；而面对后者，我们既不知道一个问题是否有答案或答案是什么，更不知道应该使用什么方法来解决它。

就个人而言，我相信两人差异的本质来自于不同的文化。事实上，美国的学校可能是全球最不好的学校之一。许多其他国家的学生在很早就掌握了更难的群论、微积分的内容，而同龄的美国学生甚至还在学基础代数。然而，美国的公立学校仍然培养了非常多优秀的理论物理学家，这是为什么呢？当我的儿子在美国公立学校上小学一年级时，我对他们上课的内容感到十分震惊。几乎在最开始的时候，他们就有一节“事实与观点”的课堂，在课上他们对各种各样的论断进行辨别，判断它们到底是一个“事实”，还是仅仅是某人的“观点”。在我看来，这是教育很重要的一个组成部分。粒子必须具有电子电荷的整数倍，这是一个事实，还是观点呢？

因此，我认为对学生来说，培养物理直觉非常重要，这也是我写这本书的原因之一。那么，如何获得物理直觉呢？在书中我提到，主要有两种方式：一些人与生俱来，一些人则通过不断地练习获得。有些人觉得物理直觉是培养不了的，它只能通过大量的计算以经验的形式获得。我不这么想。当你每次进行计算的时候，应该首先思考其结果应该长成什么样子。同时，在一周、一月或者一年后，尝试在你的脑中重复这一计算过程。不动笔不用纸，或许你会被逼着抓住问题的本质，而忘掉那些具体的数字。另外，你也应该阅读那些具有物理直觉的人写的书，例如 Purcell 或者 Feynman。我建议学生应尽量避免数学的形式化细节，像清理电脑那样整理你的脑袋，删去不必要的文件：当我在哈佛念研究生时，我的教授 Sidney Coleman 曾对我说，若你希望做粒子物理的研究，那就忘掉你所有学过的所有偏微分方程的内容，将这些从你的脑中删去，因为在粒子物理中，“猜测”（guessing），或者说“直观（intuition）”，更为重要。

我对学生的另一个建议是，不要相信那些告诉你物理和数学“一样”的话。数学和物理思考的方式、解决问题的手段，都大不相同。实话实说，每当我听到某个主修物理的同学在辅修数学时，表面上我会说好，这不错；但在我心里，我都“眉头一皱”，且我认为一些美国最好的大学负责审核研究生申请准入的老师和我有一样的感受。想要同时念好数学跟物理几乎是不可能的——当然，也完全可能存在例外，说不定正在屏幕前的你就是那个例外。但是对绝大部分的人，尤其是年轻学子和研究生，我的建议是优先专注物理。在历史上，我认为可能生活在十八到十九世纪的高斯是最后一位对数学和物理都能做出杰出贡献的学者了。如果你除了物理之外想学点别的什么东西，我建议你学和物理完全不相关的内容。例如，我在普林斯顿时同时修了和物理相关课程一样多的艺术史的课程。我当时就想，我这辈子都会做物理，但有系统地上艺术史的课程就这几年在校时期，要好好学习和掌握。

当然，我从不认为精细的计算不重要。当所有具体的数字和符号在计算的最后都正确地排列在一起时，我也会非常开心。在过去的六七年内，冬季学期我开设了“物理与猜算”（Fly by Night Physics）这门课程，而春季学期我会教群论；前者都使用约等号，后者都使用等号。我对两个符号都很喜欢，但我觉得，物理学生应先学会前者，再学会后者，而不是反过来。最重要的是，物理应该是愉快、有趣的，不然为什么学习物理呢？

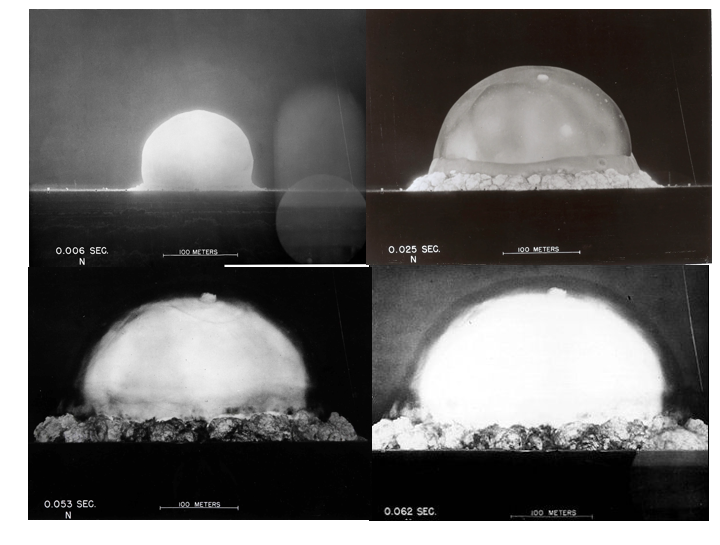
二战后，英国政府向美国政府询问有关原子弹的资料，想要了解一次爆炸会释放多少能量。但美国政府不肯提供相关的信息，因此英国人也很生气。但后来，美国政府的一个工作人员将原子弹爆炸时的照片发表在了一本普通杂志上，且这些照片还给出了拍摄的时间信息以及蘑菇云的大小。仅仅通过这四张流传出的照片，英国著名的物理学家 Taylor，还有一位苏联物理学家，就能立即确定爆炸释放了多少能量。许多人或许会认为，要估算释放的能量必须有一定的核物理知识才行。然而，我们只需要知道爆炸是“瞬时”的，且爆炸源是一个点就行了，剩下的物理过程仅仅是中心的热空气推动外部的空气不断扩张而已。因此，这些照片提供的信息已足够了。这就是我想强调的，要抓住问题的物理实质，判断哪些知识和条件是相关的。

大家也都知道，Planck 在很年轻的时候就注定会被整个物理学界永远铭记，因为他可以说是整个量子力学的创始人之一。我也曾问我的学生：Planck 是如何推出黑体辐射公式，开启量子物理的？或者说，他“推出”了黑体辐射公式吗？从什么条件出发“推出”的呢？黑体辐射公式是量子力学的一个推论，但那个时代，量子力学还不存在。Planck 得出黑体辐射公式仅仅是在他的物理直觉以及对实验数据的掌握下做出的一个猜测，且他非常大胆地引入了一个新的物理常量——现在当然被称作 Planck 常量，这里面用到的所有数学工具只有微积分而已。

再如，玻尔是如何推出氢原子基态的能量的？“推出”？怎么“推出”？那时看来，他的结论几乎纯粹来自于猜测，从（当时）物理的角度来看完全没有任何意义。Otto Stern 和 Max Laue 甚至曾发誓，若玻尔这些没有意义的物理结论是正确的，他们就退出物理学界；当然了，这两个人最后也没有退出物理学研究，且都获得了诺贝尔奖。玻尔那时需要用一个公式求解两个变元——任何学过高中数学的人都知道这是不可能的。但他根据量纲分析，把其中角动量对应的变元替换成了具有相同量纲的 Planck 常量，再利用牛顿的经典物理学，幸运地推导出了量子物理的结果。现在，任何学过一点量子物理的人都知道，氢原子基态的角动量应该是零，而不是 Planck 常量。但在物理学的发展过程中，玻尔和能准确计算氢原子基态角动量的学生，谁更重要呢？

再来看一个更现代的例子。Laughlin 因为他写下了分数量子霍尔效应所对应的多体波函数而获得了诺贝尔奖，现在这一波函数也被称作 Laughlin 波函数。“写下”？如何“写下”？对于那些在量子力学课上得 A 的学生，他们擅长：给我一个哈密顿量，我能求解其对应的波函数。然而，Laughlin 先写下了波函数长什么样，随后才来构造一个哈密顿量。他写下这个多体波函数的灵感来源于哪里呢？Laughlin 曾经给我看了他一个很厚的笔记本。他先求解了一个平面电磁场下两个电子的波函数，然后求解了三个电子的波函数——这已经非常复杂了，随后再尝试求解了四个电子的波函数，而这几乎是不可能的。而对于量子霍尔效应，其涉及的电子数目是 10²³这一数量级的。他的笔记写满了厚厚的整个笔记本。由此可见，他的直觉也来自于努力计算许多具体的例子。更有趣的是，Laughlin 之后也跟我讲过，他当时并不知道任何与量子霍尔效应有关的物理内容。一位世界知名的日本物理学家在量子霍尔效应领域工作了三十多年，一直尝试解决这个问题，但这位日本物理学家的所有方法都是基于整数量子霍尔效应的，这也是当时标准的物理理论。然而，Laughlin 在不知道哈密顿量的情况下猜想的波函数所带来的霍尔效应并不是整数的，而是分数的，这非常不可思议。事实证明，这一看起来“漫无边际”的猜想才是更为正确的答案。

徐一鸿教授根据他多年研究、教育，以及与学生打交道的观察和经验，做了一场非常精彩的演讲。我自己的一条体会是，徐教授希望一开始在本科教育的时候，就能着眼于培养学生今后在研究、探索未知领域时所应具备的能力。对我们而言，在教学过程中应不断提醒学生关注基本的物理图像，在大量的计算中清晰地理解前后的因果关系，这是非常重要的。这一点对中国、亚洲，甚至全球的学生都是有普遍意义的。

徐教授还讲述了如何培养物理直觉。徐教授提到了两种观点，我也有同样的感受。一类人的确有很强的天赋，另一类人也可以从长期的经验和体会中突然领悟出大胆的猜想。我想徐教授写这本书也是希望广大读者能耳濡目染、受到熏陶，从物理图像的角度感受到什么是物理的直观。然而，借着徐教授书中提到的很多例子，我也想提醒大家：例如Feynman，他可能让别人以为他做什么工作都很轻松容易，但事实上他私底下也有非常多的计算；再如 Laughlin，他大胆地猜出了一个波函数，但他的计算也占满了厚厚的一个笔记本。同样，我也希望读者想到，徐教授在写这本书的时候一定也做了很多的笔记和思考。因此很多时候，强大的计算能力也是十分重要的。只是在计算时，不能总局限于具体的细节，而应不断地思考计算的整体目标，把握其整体脉络。

徐教授的同事和朋友都亲切地称他为 Tony，我这里也仅就听 Tony 的发言以及自己阅读这本书的感受，做几点补充。

首先，Tony 这本书开篇就引用了前面提到的 John Wheeler 的话：Never calculate unless you know the answer。我相信对大部分物理学家而言，这是对的。但 John Wheeler 是美国人，使用英文非常精炼；在我看来，如果对这句话稍加补充的话，应该是：Never calculate unless you know the possible answer，即你至少应该知道什么是可能的答案。如果你在动笔计算前已经知道唯一正确的答案，当然更了不起，但很多时候物理学家面对一个问题仅仅是猜出可能的答案。

我可以举一个关于 Tony 的同事 David Gross 和 Frank Wilczek 的例子。他们在计算非阿贝尔规范理论的重整化β -函数时，David Gross 自己也谈到他们犯了许多错误，并且在最后写文章检查时才发现写错了一个符号，最终正确的结果应该是负的。但我想，他们两人在计算前至少知道两点。第一，计算这个 β -函数的物理后果非常重要；第二，最终的结果要么为正，要么为负。当然，若结果为负，则对于物理学是更具有革命性的意义。因此，作为对 Tony 所讲内容的补充，我想表明即便物理学家不知道唯一的答案，也一定会在进行详细计算之前去猜测可能的答案。

其次，我也想强调一下 Tony 所言的做研究和做作业之间的区别。我自己在清华和上海交大都讲授了很多年量子场论课程，我是不赞同当堂闭卷考试的方式。我做学生时的量子场论课程是在北大上的，当时的清华还没有开设这门课。依照北大的风格，这些课程都需要当堂考试。虽然我也考了很好的分数，但我意识到，像量子场论这样面向物理学前沿研究的课程，闭卷考试其实没有太大意义。正如 Tony 在书中强调的那样，研究跟作业或考试最重要的区别是，后者解决的都是知道答案的问题。我们中国学生从中学到大学经受的训练，特别是高考的训练，大多培养的都是解决后一种问题的能力。

另一个让我深受启发的例子，是刚才 Tony 提到的 Gell-Mann 和南部阳一郎之间的区别。前者是非常具有美国风格的物理学家，后者在日本博士毕业之后也到了美国，应该说兼具东西方的特点。南部阳一郎在多年的工作后已经非常接近对夸克的完整描述了，但为什么没有提出夸克具有电子电荷分数倍的猜想？Tony 没有特别强调，但我想这一例子是想表达东西方文化的差异对物理学家思考的影响。我也想到了李政道和杨振宁两位先生提出宇称不守恒的例子。两人都在东方长大，但读博期间就到了美国。他们提出的宇称不守恒假说及其检验方案是物理观念上的一次革命。只要想到了这一点，剩下的内容就会水到渠成，而且他们原始的文章是唯象的，并没有发展关于宇称不守恒的任何基础性理论。但问题是，为什么这样的观念当时的物理学家没有任何人想到或者敢于提出，而且即使提出之后也几乎无人相信？著名理论物理学家 Pauli 甚至为此打了赌，认为宇称不守恒一定是错误的。这恰恰体现了 Tony 在演讲中提到的“事实”与“观点”之间的区别。现有教科书上的部分内容其实并没有被实验直接证实，或者说仅仅是从现有观测所得到结论的推广，因此只能是某种观点。未能严格分清事实与观点之间的区别，我想可能是南部阳一郎没能突破原有观念束缚的其中一个重要原因。

我曾经也读过赵凯华教授的《定性与半定量物理学》，这本书和 Tony 想强调的另一要点是一致的，就是要学会猜算。猜算不是简单的数值估计，而是依据物理直觉分清什么是问题的本质，而省略不必要的细节。因此，我也强烈推荐大家阅读徐教授的这本书。遗憾的是，据我所知国内的大学还没有类似的物理课程。我们真的应该依照此书的内容开设相关的物理课程。

最后，我对 Tony 提到数学与物理之间的区别也是非常有趣而重要的一个问题。Tony 说这两者非常不同，甚至不相信有人能同时对两个领域做出杰出的贡献（至少在高斯之后），当然他讲了也有例外。我自己阅读数学家的文章或者与数学家交流的感受是，数学家的证明有时非常冗长，动辄一两百页，例如 Tony 在UCSB（加州大学圣塔芭芭拉分校）的数学同事张益唐先生最近在朗道-西格尔零点问题上的突破，其论文就有一百多页。但我想，数学家在写这么长的证明之前，一定也猜出了答案，并且产生了总体的证明思路，才能一步步完成具体的推导与证明。因此，在我看来，数学家也是需要直觉的，只是研究数学和物理所需要的直觉可能有所不同。

数学和物理的另外一个区别可能是数学的问题至少都是严格定义的，你只需证明或证否它即可。但是对于物理而言，有时连问题在何处人们都不清楚。在这种情况下，我们更需要深刻的物理直觉去发现问题和抓住问题的实质，才能有所突破，这也是 Tony 不断强调的。