在明清时期的笔记文献中，记载了很多可用现代数学解释的内容，或为工程所用，或为游戏娱乐，展现了古人的智慧。

撰文 | 刘钝

卷帙浩繁的中国古代笔记中含有丰富的科学史料。本文从明清笔记中披检出的一些材料，涉及了数学中的某些思想、原则或方法。从现代数学的视角来考察、分析这些史料，将有益于拓宽中国数学史研究的视野，特别是将有益于揭示数学的发展与社会文化背景的关系。

报恩塔与标准化思想

标准化应属于现代管理科学的范畴，但是它的具体操作往往与计算方法、数理统计、误差分析等数学分支相关。标准化的思想在中国肈源甚古，《考工记》《营造方式》《天工开物》等工艺技术经典为一代代工匠提供了制作规范，明末张岱（1597-1679）《陶庵梦忆》所记金陵（今南京）报恩塔的掌故，则提供了在建筑上利用标准化思想的有趣例子：

“报恩塔成于永乐初年，非成祖开国之精神，开国之物力，开国之功令，但胆智才略足以吞吐此塔者，不能成焉。塔上下金刚佛像千百亿金身。一金身，琉璃砖十数块凑成之，其衣褶不爽分，其面目不爽毫，其须眉不爽忽，斗笋合缝，信属鬼工。闻烧成时，具三塔相，成其一，埋其二，编号识之。今塔上损砖一块，以字号报工部，发一砖补之，如生成焉。”（张岱：《陶庵梦忆》，卷一，上海古籍出版社，1982年版，第2页。）

“成其一，埋其二，编号识之。”在这样大型的砖瓦建筑中应用标准化思想，我们不能不对设计者的独具匠心表示钦佩。

被张岱称为“中国之大古董，永乐之大磁器”的报恩塔，历经四百五十年风雨，终于清咸丰年间毁于战乱之中。近来有关部门在该塔原址发掘出若干残砖并有意恢复这一古迹的原貌，不知能否证实以上关于“编号识之”的传闻？又若能找到当年明工部保存的另外两套砖瓦，报恩塔的复原岂不易如反掌？

移棋相间与镶符理论

移棋相间大约是兴起于明末清初的一种智力游戏，其规则是：将黑白棋子各n（n≥3）枚，左右分列成一行，每次将相邻两子一并移至两个相邻空格之中，经若干次移动使棋子变成连续排列的黑白相间形式。清康熙年间褚人获（1635-1682）的《坚瓠集》对此提供了如下记载：

“幼年见友人胡砺之将黑白棋子各三枚左右分列，三移则黑白相间。余因问曰：‘多亦可移乎？’砺之曰：‘自三以至于十外，皆可移。多一子则多一移。’余归试之，自三以致于十果相间不乱。今已三十余年，偶雨窗复试，忘其大半，因绎数四始得就，恐岁久复忘，作歌以纪之。曰：三子从根起，二三望前移；四子根空一，从根还空位，二三复归所，未子向前备；五子前后各空一，黑白从中移向前，二三黑白还空位，根头二子自天然；六子从根各空一，四五二马向前行，五六二子归空位，二三黑白望空存；七子从根只空一，二移右起三四行，四子相连从中去，四移右数六七轮，五移邻子归空位，二三去兮末子登；八子从根各空一，五六左右交互换，五移六七向前轮，六移七八补缺断，二三黑白归空处，就是儿童也不乱；九子从根亦空一，二移左断四五通，三移六子从中去，四子相连亦去中，五移九十归空位，右一降兮左一逢；十根空一前补后，三移五六向前通，四移六七归空位，五移四子去其中，六移九十还归处，壁邻二子补其空，八移五六向后去，二三归空末子逢。”（褚人获：《坚瓠集》，戊集卷一，柏香书屋石印本。）

文中提到的胡砺之显然是一个精于此道的行家，他提出的“多一子则多一移“的命题相当于说最少移动步数等于棋子的对数n。褚人获关于三至十对棋子移动规律的歌诀也是正确的。兹以n=3为例：

但是褚人获的歌诀仅是一种帮助记忆的手段，其中的步骤往往不够完整且所用术语有含糊不清之嫌，若非谙熟此道者，恐怕难以顺利移动。清末朴学大师俞樾（1821-1907）及其夫人季兰对此游戏又作了进一步的研究，他们不但给出了十一至二十对棋子的具体移法，而且提出了记录移动程序的简便方式。俞樾在《春在堂随笔》中写道：

“长洲褚稼轩《坚瓠集》，有移棋相间法。以黑白各三子，三移，而黑白相间，自三子至十子皆然，多一子则多一移耳。余试之，良然。而内子季兰复推广之，自十一子至二十子。余恐其久而忘也，因笔之于此。”（俞樾：《春在堂随笔》，卷一，江苏人民出版社，1984年，第16页。）

接着作者笔录了从三至二十对棋子的移动程序，例如对上述三对棋子的情况，俞樾记为“左一、二，左四、五，左一、二”；“左一、二”表示将左起第一、二两枚棋子移至右方空位中去（第一步就是移至最右端），“左四、五”表示将左起第四、五两枚棋子移至右方空位中去，又一个“左一、二”同样表示将左起第一、二两枚棋子移至右方空位中去，至此三对棋子已成黑白相间的排列。同理，“右某某”则表示将右数相应两枚棋子移至左方空位（第一步移至最左端）。兹以n=15为例，移动程序记为：

“左二、三，右十三、十四，左六、七，右九、十，左十二、十三，右五、六，左九、十，右十四、十五，左十五、十六，右十、十一，左十一、十二，右六、七，左五、六，左二、三，右一、二。”（俞樾：《春在堂随笔》，卷一，江苏人民出版社，1984年，第17页。）

早在三十年代初，数学史家李俨（1892-1963）先生就对移棋相间问题产生了兴趣，他曾推测这一民间游戏与八卦或幻方有关，但没有述及上述史料。同时限于组合数学在当时尚未引起世人充分注意，研究者也不可能对这一问题的数学内涵展开更细致的讨论。近年来有人将移棋问题作了进一步推广：即将黑、白两色棋子推广成多色，将每次移动相邻两子推广为每次移动相邻P（P可为1）子，并得出了两色棋子每次“移2”的普遍解法及其最少步数等于棋子对数n的证明（赵缭、李俨：“黑白交错图”，《学艺》，第12卷（1932）第10号， 第53-64页。）。

从现代组合理论上来讲，移棋相间问题属于镶符理论的范畴，其实质是在某种特定的组合规则之下将一种序列重新组合成另外一种序列，例如将若干个以一维形式存贮于计算机内的数据按照类别重新分别存贮，又如用移位法来编制或破译密码，其原理都与移棋相间问题有某种相通之处（胡著信：“镶符问题的历史渊源和现代发展”，《中国数学史论文集》（二），山东教育出版社，1986年，第56-64页。）。这自然是古代文人仕女们始料不及的。

七巧图与出入相补原理

七巧图的起源尚无定说，在西方它被称作“唐图”（Tangram）。可以确信的是七巧图及与它类似的拼图游戏如燕几图、蝶几图或益智图，在明清两代曾于民间广为流行。清代道咸年间陆以湉（1801-1865）于《冷庐杂识》中记道：

“宋黄伯思燕几图，以方几七，长短相参，衍为二十五体，变为六十八名。明严澂蝶几谱，则又变通其制，以勾股之形，作三角相错形，如蝶翅。其式三，其制六，其数十有三，其变化之式，凡一百有余。近又有七巧图，其式五，其数七，其变化之式多至千余。体物肖形，随手变幻，盖游戏之具，足以排悶破寂，故世俗皆喜为之。”（陆以湉：《冷庐杂识》，卷一，中华书局，1984年版，第60页。）

七巧图系由一块正方形切割为五个小勾股形、一个小正方形和一个小平行四边形而成，利用这些图形的拼补移动，可以构成种种奇妙的造型来。它的形制和功能很容易使人联想起古代数学家证明几何定理所用的弦图来，见图1-2。

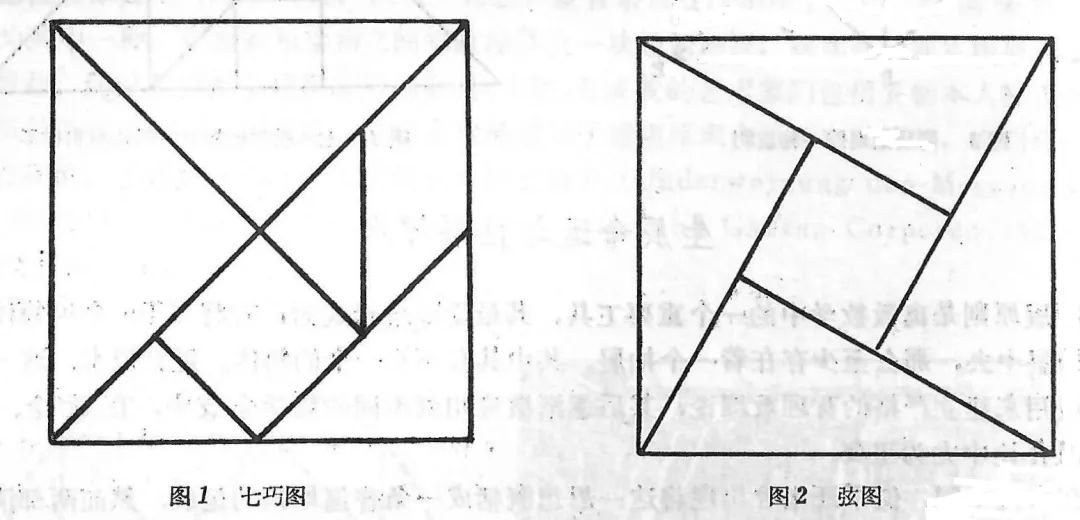
利用七巧图，同样可以阐述说明若干平面几何关系，其原理就是古代数学家刘徽、赵爽等人创用的出入相补原理。刘徽《九章算术注》中证明勾股定理的图示早已亡佚，今日只存如下的简要注文：

“勾自乘为朱方，股自成为青方，令出入相补，各从其类，因就其余不移动也。合成弦方之幂，开方除之，即弦也。”（钱宝琮校点：《算经十书》，上册，中华书局，1963年版，第241页。）

就下面图3中的勾股形ABC而言，股方ADBC由两个较大的勾股形组成，不妨想象它们被涂成青色；勾方CBEF则由其余的五块小图形所拼成，同样可以想象它们都被涂成赤色，顺序将Ⅰ（“青出”）和Ⅱ、Ⅲ、Ⅳ（以上三者为“朱出”），分别移至I’（“青入”）和II’、III’、IV’（以上皆为“朱入”）的位置，于是得到一个大的正方形ABFG，这就是弦方（七巧图原式）。图4则是由七巧图拼成的平行四边形和梯形，借助它们也不难验证这两类几何图形的面积公式（略）。

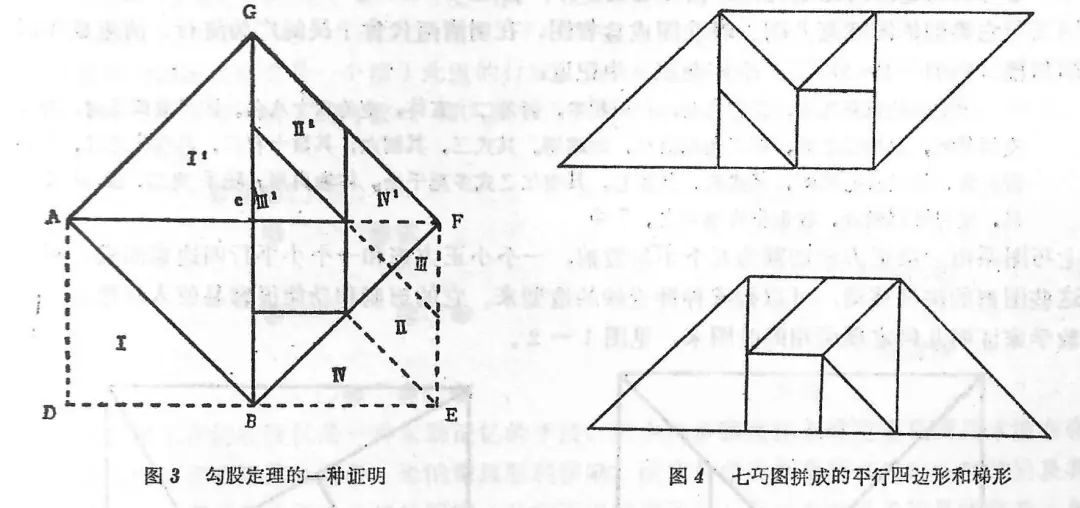
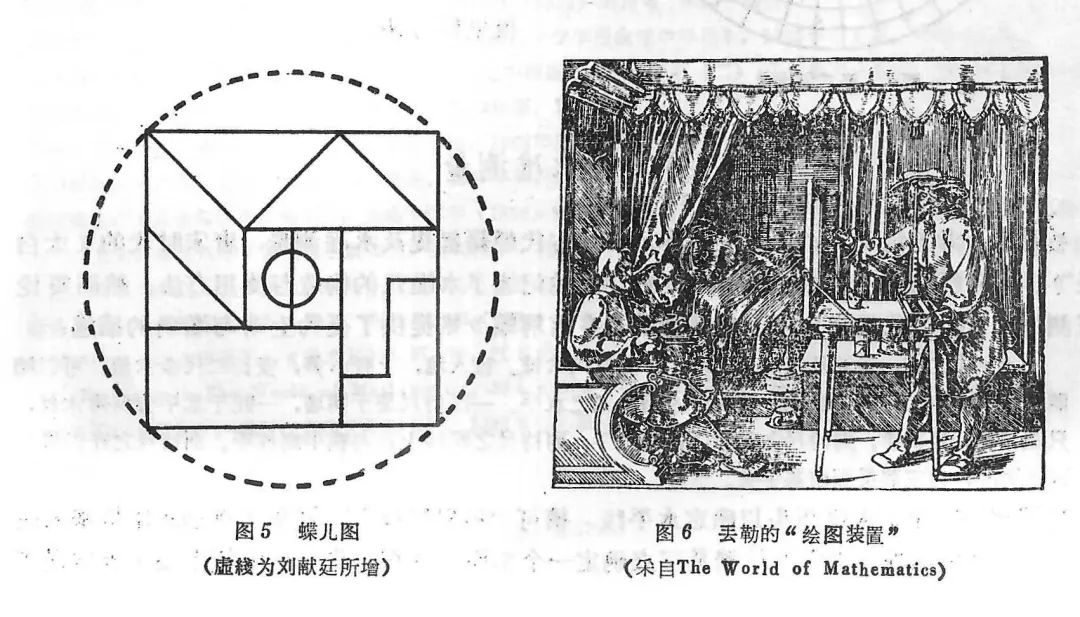
据此或许可以推测，七巧图的发明者，如果不是一个数学家，起码也从类似于出入相补原理这一思想获得过启发与灵感。对此，康熙年间的知名学者、通晓数学的刘献廷（1648-1695）在第一次见到蝶几图（图5）时的震惊之情是颇能说明问题的，他在《广阳杂记》中写道：

“十三只做式图一册，宗夏得之芜湖市者，不知作者何人，发明何事，有图无书，帷标名像，非我佳人，莫之解也。宗夏留以俟予，予见之而魂惊魄惕，此予向者意地中固有之局，何斯人之先得我邪？其图以一平方面，截为十三块，或长方，或半长方，或锐角或钝角；辗转挪移，互相拼凑，或为圭形，或为磐形，或为屋宇形，或为桥梁形，或为飞燕形，或为舞蝶形，此宇宙之殊形异相，总不出其范方矣。予意取一平围板，纵横界画，如棋罫然，而经纬皆以百分为率，以便算也。然后如其式而截之，增减离合，以度求数，数无遁情矣。若更于大方之外，增四弧矢，如《周礼》衍羡之法，以证围径真旨，而方田、少广诸章，其余事耳。呜呼异哉，安得遇斯人而与之谈度数之学哉？”（刘献廷：《广阳杂记》，卷三，中华书局，1957年版，第116页。）

生辰命运与抽屉原则

抽屉原则是离散数学中的一个重要工具，其最简单陈述形式为：若将多于n个的物体放到n个抽屉中去，那末至少存在着一个抽屉，其中有不止一个物体。近世以来，这一原则首先被用来建立严格的有理数理论，其后逐渐被应用到不同的数学分支中，在数论、集合论、组合论中尤为重要。

在古代中国，似乎还未曾出现将这一思想概括成一条普遍原则的记载，然而两部清代笔记中却隐含着应用这一思想来分析问题的例子。乾隆年间阮葵生（1727-1789）力斥生辰八字之说，其《茶余客话》中写道：

“人命八字，共计五十一万八千四百，天下恒河沙何止于此，富贵贫贱寿夭势不能同。即以上四刻下四刻论，亦止一百三万六千八百尽之，天下之人何止千万，亦不能不同。且以薄海之遥，民物之众，等差之分，谓一日止生十二种人或二十四种人，岂不厚诬？”（阮葵生：《茶余客话》，卷十八，光绪十四年（1888）铅印本。）

盖以六十甲子纪年纪日，十二干支纪月纪时，其不同的组合总数为60×12×60×12，即518400种；即使将一个时辰分成上、下两半也不过1036800种。这就是“抽屉”数，而作为“物体”的“天下之人何止千万”，可见必有八字全同而“富贵贫贱夭寿不能同”者在。这里正是暗用了抽屉原则。

同书又以两个实例来说明八字之“厚诬”，其一为“（北宋）蔡京八字丁亥壬寅壬辰辛亥，生庆历中。后六十年至大观改元丁亥，东都有郑氏贷粉者以正月初五日辛亥生，八字与京同，人皆异之。后年十八醉骑马坠金池死。”其二称“明英宗八字与布衣沈周、知县卢钟皆同。”

咸丰年间又有陈其元（1812-1882）驳斥星占之说，其《庸闲斋笔记》云：

“余最不信星命推步之说，以为一时生一人，一日当生十二人，以岁记之则有四千三百二十人，以一甲子计之止有二十五万九千二百人而已；今只一大郡以计，其户口之数已不下数十万人（如咸丰十年杭州府一城八十万人），则举天下之大，自王公大人以至小民何啻亿万万人？则生时同者必不少矣，其间王公大人始生之时必有庶民同时而生者，又何贵贱贫富不同也？”（陈其元：《庸闲斋笔记》，卷七，同治十三年（1874）刊本。）

这里以十二辰、三百六十日、六十甲子计之，共得“抽屉”数12×360×60，即259200，比当时杭州城的居民数还要少得多，由此可见星命决定贵贱贫富是不可信的（有关这一主题的最早记录可能见于宋代费衮的《梁溪漫志》卷九之“谭命”条，又见清代钱大昕（1728-1804）《潜研堂文集》。——作者补识）。

临书桌与透视法

透视学兴盛于欧洲文艺复兴时代的艺术大师们，它与几何学有直接的关系。

清代有人评论西画曰：

“西洋善勾股法，故其绘画于阴阳远近，不差锱黍。所画人物屋树，皆有日影。其所用颜色与笔，与中华绝异。布景由阔而狭，以三角量之。画宫室于墙壁，令人几欲走进。学者能参用一二，亦具醒法；但笔法全无，虽工亦匠，故不入画品。”（ 邹一桂：《小山画谱》，《美术丛书》第二册，江苏古籍出版社，1986年版，第527页。）

作者显然未见过西画中的精品，同时他以中国画的“笔法”去衡量西画也是荒唐可笑的，然而“以三角量之”、“虽工亦匠”等语，用来形容某些西洋画家追求极度精确透视效果的作法倒是十分贴切的。

德国画家丢勒（A.DÜrer, 1741-1528）就曾亲自设计制作了数件“绘画装置”，图6即为其中一种：在画家与景物之间垂直地竖立一块透明画板，画家在一个固定距离处单眼瞄准景物，同时在画板上描出相应的载景。当然，有成就的艺术家包括丢勒本人都不会用这种呆板的方法去作画，但是这一装置直观地显示了透视原理在绘画中的应用，在当时是起了一定作用的。丢勒本人还在其《测量四书》（Four Books on Measurement，1525）一书中加以介绍。

无独有偶，中国古代也有人设计过类似的装置，不过不是用来绘画，而是用来习字。生活于明清之际的学者周亮工（1611-1672）在其《书影》中引黄庭坚（1045-1105）与人贴云：

“唐临夫作一临书桌子，中有抽屉，面两行许地，抽屉中置灯临写摹勒，不失秋毫。”（周亮工：《书影》，卷五，古典文学出版社，1957年版，第133页。按周亮工所引出自黄庭坚帖《因树屋书影》。）

唐临夫是一个人，还是泛指唐代的临书者，仅以这条材料尚难断定。可以肯定的是，至迟于北宋年间，就有人发明制作了一件与丢勒的“绘画装置”原理全同的临书桌，以其“向灯取影，以远近为大小”，这是在艺术领域借助机械手段获得透视效果的较早实例。

圆式围棋与极坐标思想

坐标的应用独立并早出于解析几何。古希腊天文学家为了描述日月星辰的运动而引进了球面坐标系统，中国古代地理学家为了绘制地图引进了平面网络坐标系统。按照我们现今的理解，一种坐标系统的有效性有赖于其上的点能与一个数组建立一一对应关系；在这种意义之下，起源于中国的围棋及其记谱方式也是一种平面网格坐标系统。令人感兴趣的是，明清之交有人发明了圆式围棋，周亮工《书影》在摘引了东汉马融（79-166）的《围棋赋》后记道：

“近余集生中丞创为圆棋盘，然其法与方棋盘亦无大异。”（周亮工书

影》，卷四，古典文学出版社，1957年版，第157页。）

“集生中丞”疑指明万历进士陈子壮（1596-1647），陈子壮字集生，明亡后投永明王被封为东阁大学士；周亮工是明崇祯进士，明亡后亦一度南奔，他们两人是有机缘相识的。至于圆棋盘的形制，笔者揣度由18条经线和10条纬线交织而成（图7），相邻两经线的距离适为10度，而其组成的格点总数亦为361，与方棋盘无异。十分显然，这种圆式围棋的记谱法是一种极坐标方法。

造屋与水准测量

《周礼·考工记》《史记·夏本记》等古代典籍都提及水准测量，唐宋时代的《太白阴经》《武经总要》《营造法式》更详细记述了水准仪的构造与使用方法。然而要论造室测平之术，清代道光年间李光庭所撰《乡言解颐》则提供了更为生动与准确的描述：

“测平之法，于地基四隅垒小墙，中置三尺木锥。锥入地，上有小笋，安长二尺余木槽，可以随隅转移。约宽二寸，以容水，两头浮木鸭，谓之水平。一匠持尺墨于隅墙，一匠于水平旁斜倚木杖，只眼视鸭。复其手，则持尺之匠移下；翻其手，则持尺之匠移上；与鸭平则挥手。而持尺之匠以墨尺画墙为准，以三隅反而地基平矣。”（李光庭：《乡言解颐》，卷四，中华书局，1982年版，第57页。）

“木鸭”即准星，浮于水槽两头以确定水平线。槽可“随隅转移”，避免了挪动底座带来的误差。“以三隅反而地基平”的依据是三点确定一个平面，这在前代文献中似乎还未曾被提到过。“只眼视鸭”、“复其手”、“翻其手”等语，则栩栩如生地刻划了当时工匠定水平的操作细节。

民间歌诀与大衍求一术

大衍求一术萌芽于南北朝时代《孙子算经》之末题，至南宋秦九韶（1202-1261）而蔚然大观。这一问题流入民间后，先后有“孙子算”“鬼谷算”“隔墙算”“翦管术”“秦王暗点兵”“韩信点兵”等繁多名称。有些著作还载有解题的歌诀。褚人获《坚瓠集》所引名称与歌诀内容尚未被研究者征引，今转录于下：

“《挑灯集异》有隔壁笑诀：三人逢零七十稀（每三作一数，三数之余，或余一则作七十，余二则作一百四十，如无余不必论），五马沿盘廿一奇（一作五人折桂廿一枝，每五作一数，五数之余，或余一则作廿一，余二则作四十二，余仿此）,七星约在云霄里（每七作一数，七数之余，或余一则作十五），一百零五定为除（盖前后总计积数若干，这一百零五或二百一十即除去，余所存数即其手中所握之数也。）（褚人获：《坚瓠集》，戊集卷一，柏香书屋石印本。）

明清笔记浩如烟海，限于学识阅历，笔者仅仅接触了其中的一小部分，挂一漏万所难免，所引材料亦恐有不妥之处，敬希方家一并教正。

本文原载《中国科学技术史料》1989年第10卷第4期，原标题为《若干明清笔记中的数学史料》。