近日，韩国量子能源研究中心一研究组在预印本网站刊文，宣称使用改性铅-磷灰石晶体（LK-99）实现临界温度约126.85℃的常压室温超导，引发全球关注。文章从临界温度、零电阻率、斯迈纳效应等多方面论证，并称这一发现将“开启人类新时代”。同时，他们的工作立即受到质疑，甚至被网友发现作者署名的“罗生门”，剧情走向扑朔迷离。由于此前室温超导风波主角Ranga Dias遭遇连续撤稿，人们对此次发现更谨慎——让子弹飞一会儿。实际上，无论是实验还是理论方面，超导领域仍面临许多挑战，本文主要介绍高温超导机理方面物理学家面临的重要问题，期待迎来真正的突破。

撰文 | 向涛（中国科学院物理研究所、中国科学院大学物理科学学院、量子物质科学协同创新中心）、  薛健（中国科学院物理研究所、中国科学院大学物理科学学院）

来源 | 本文发表于《物理》2017年第8期

摘要

自1986年铜氧化物高温超导体发现以来，高温超导研究取得了丰硕的成果，确定了高温超导材料的相图和超导配对的对称性，发现了赝能隙、电荷自旋分离、线性电阻、强超导位相涨落等大量新的物理现象。但是，高温超导机理依然还是一个谜，高温超导材料中发现的大量反常量子现象也不能在已有的固体量子理论的框架下得到解释。要解决高温超导问题，必须发展新的实验探测技术和新的量子多体理论及计算方法。特别是要发展能够直接调节和探测电子与固体中各种元激发相互作用的实验探测技术，从相互作用的源头来直接探测并判定高温超导电子配对的机理。

01引言

高温超导是20 世纪最伟大的发现之一，这项发现不仅为超导的应用开辟了新的方向，同时也为我们揭示了一个新的微观量子世界，向传统的固体量子理论提出了挑战。其中最具挑战性的问题，就是高温超导机理问题，这也是上个世纪遗留下来，未解决的重要科学问题之一。

超导现象最早是由昂纳斯 (Onnes) 等在1911 年发现的。第一个超导微观理论是1957 年由巴丁 (Bardeen)、库珀 (Cooper) 和施里弗 (Schrieffer) (BCS) 三位科学家建立的。他们的理论对金属或合金超导体的物理性质给出了非常漂亮的解释。

在BCS理论中，超导是由于固体中电子在某种吸引相互作用下形成具有一定玻色子特性的束缚态 (也称为库珀对)，然后凝聚导致的。因此，超导机理的研究，根本上讲，就是要解决以下三个问题：

1. 电子是在什么相互作用的支配下，形成库珀对的？

2. 库珀对是如何形成位相相干、凝聚变成超导长程相干的？

3. 进入超导相后，如何描述超导电子的物理行为？

对于第一个问题，BCS给出了部分回答。他们指出普通金属超导体里面导致电子配对的相互作用是电声相互作用。但是对于铜氧化物高温超导体，BCS理论没有给出答案，我们现在也不知道答案是什么，这也是高温超导机理研究需要解决的一个关键问题。

对于第二个问题，BCS 没有给出系统的回答。在普通的金属超导体中，由于超流密度很大，电子相干性很强，从配对到形成超导长程相干几乎同时发生，基本上是一配对就超导。所以对金属超导体，这个问题没有受到太大的关注。但对高温超导体，超流密度减小，超导相干性减弱，库珀对的相干过程对超导体的性质有很大的影响。电子有可能形成了配对，但未能形成位相相干进入超导态。

对于第三个问题，也就是如何描述超导态电子的物理性质，BCS给出了非常漂亮的答案，其理论框架是完备的。在超导相，电子形成了超导长程序，由于超导电子的物理性质与电子形成库珀对的过程没有太大关系，因此这部分理论无论是在金属超导体中，还是在铜氧化物高温超导体中都成立。只要知道能隙函数的对称性及其在费米面上随动量变化的函数形式，就可以根据BCS理论，对超导体的性质做非常准确的预测。

高温超导发现后，理论上很快就预测铜氧化物高温超导电子的配对具有d 波对称性。但早期的实验结果并不支持这个理论预测。第一个高温超导具有d 波电子配对对称性的实验证据，是1993 年由加拿大的Hardy 教授等通过微波实验测量磁穿透深度给出的。他们发现磁穿透深度在低温下随着温度线性变化，是d 波超导体的特征行为。随后，基于不同原理和不同方法的大量实验测量也都表明高温超导电子配对的确具有d 波对称性，根据d 波对称对高温超导体在超导相所做的理论预测也基本上都得到了实验的验证。

因此，对于高温超导而言，第三个问题已经得到解决，但前两个问题依然还是个谜。这就是高温超导机理研究所面临的困难。前两个问题之所以难解决，是因为这两个问题不仅和高温超导体的超导性质有关，而且还与高温超导体的正常态 (非超导态) 的性质有关。而高温超导体正常态的物理性质非常不正常，其中许多性质在已有的固体量子框架下都得不到基本的解释。这就意味着高温超导现象超越了已有固体量子论的理论框架，需要建立新的固体量子理论，也就是所谓的强关联量子理论，才能真正解决高温超导问题。由此可见，高温超导机理的解决，不仅标志着我们对产生高温超导的微观原因，特别是导致高温超导电子配对的机理，有了准确的认识，建立了系统描述高温超导的微观理论；而且预示着一个超越已有量子场论框架的新的多体量子理论的诞生，其重要性要远远超出高温超导研究本身。

02高温超导带来的挑战

高温超导在超导相的性质与BCS理论的预期是一致的，但正常相的性质却出现了大量反常，无法在已有的固体量子理论框架下得到解释。图1是铜氧化物高温超导体随掺杂浓度p 和温度T 的变化相图，主要包含莫特绝缘体、超导、赝能隙、奇异金属和朗道费米液体5 个相。高温超导体没有掺杂的母体材料是一个反铁磁莫特绝缘体，超导相是通过掺杂完全抑制掉这个反铁磁相后出现的。在超导相之上，欠掺杂区存在一个赝能隙，最佳掺杂区附近存在奇异金属相，在过掺杂区还存在一个与通常金属性质比较相似的朗道费米液体相。这5 个相中，除了超导和朗道费米液体相，其他的3 个相的物理性质都不能在已有的固体量子理论中得到很好的描述和解释。特别是莫特绝缘体中元激发的微观描述、赝能隙产生的物理机理、超导的位相涨落、线性电阻以及电荷—自旋分离等问题，至今不能在一个统一的框架下得到满意的解释，是解决高温超导问题的主要障碍。

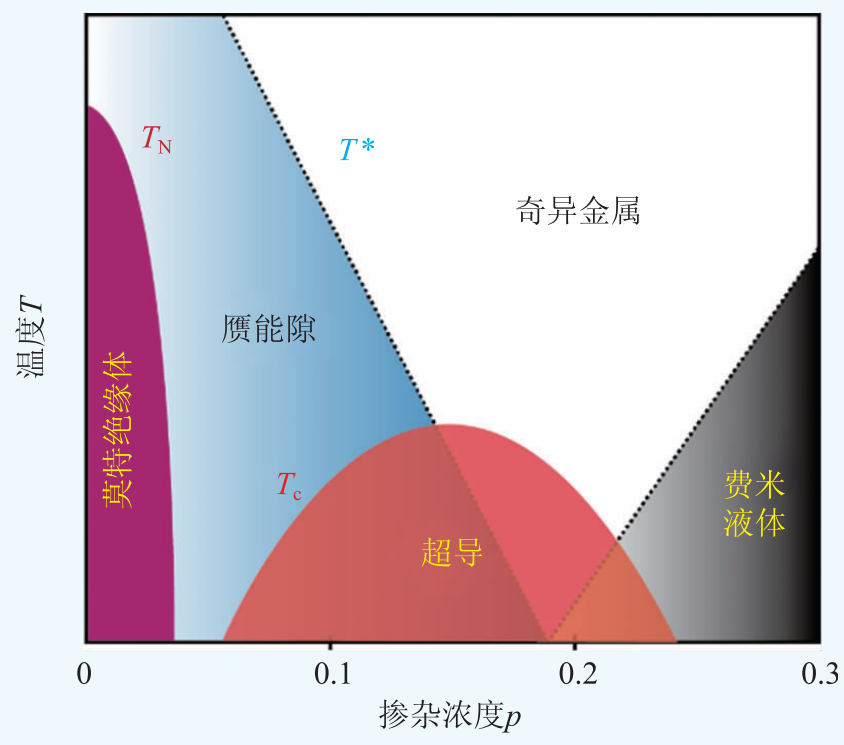
图1 铜氧化物高温超导材料的相图

2.1 莫特绝缘体

高温超导体是掺杂的莫特绝缘体，这句话不仅意味着莫特绝缘体是高温超导的母体，而且也意味着莫特绝缘体与高温超导体中观测到的大量反常物理行为具有相同的物理起源。因此，建立准确和系统描述莫特绝缘体的理论框架，是理解和解决高温超导问题的关键。

莫特绝缘体最早发现于1937 年。同年，派尔斯 (Peierls) 和莫特就指出，莫特绝缘体是由于电子的库仑排斥导致的，是一种由于关联量子效应导致的电子局域化效应。其基本图像是，当同一个晶体元胞内电子之间的库仑相互作用很强时，每个元胞倾向于只有一个电子或没有电子占据。在能带半满填充时，由于每个元胞正好有一个电子占据，电子在不同元胞之间的跳迁就会产生双占据，能量上不利，这种过程被抑制，因此电荷是局域的。这个图像是对的，但要更为系统和定量地描述莫特绝缘体的物理性质就不够了。

近年来，随着对莫特绝缘体研究的深入，理论上发现，在莫特绝缘体中，存在doublon (双占据子) 和holon (空穴子) 两种新的元激发。双占据子带负电，空穴子带正电。莫特相变是这两种元激发相互作用的后果：如果这两种元激发完全自由运动，系统呈现出金属行为；但如果双占据子与空穴子形成类激子束缚态，电荷运动被抑制，系统呈现绝缘行为。现在理论上还不清楚如何准确描述这两种元激发，也不清楚如何能够在实验上观测到这两种元激发。

在掺杂的莫特绝缘体中，由于强库仑相互作用的存在，增加一个电子要比拿走一个电子(亦即增加一个空穴)所需的能量高，因此电子和空穴激发是不对称的。这个性质体现在扫描电子隧道谱上，就是正偏压下谱线的强度要小于负偏压的强度。这种谱线强度的不对称在超导相中也观测到了，说明导致莫特绝缘体的关联效应对超导的性质也有影响。

2.2 赝能隙现象

赝能隙现象出现在高温超导体的正常相中。当赝能隙出现时，电子的激发在费米面的某些片段上存在能隙，导致元激发态密度的抑制。赝能隙是高温超导体中发现的一个让人非常困惑的物理现象，起源还不清楚。这种现象最早由Alloul等在高温超导材料的核磁共振实验研究中发现，开始被认为是一种“自旋能隙”效应。后来Loram等在电子的比热的测量中也发现存在这种现象，证明这种“能隙”不仅仅只是在自旋激发中存在，因此被称为赝能隙。

赝能隙有许多表现形式。其中一个最令人困惑的就是在赝能隙相中，电子的费米面不封闭，是一些片状的费米弧，由此造成系统热力学和动力学性质的反常。图2(a)是Y0.85Ca0.2Ba2Cu3O6+x 超导体的比热随温度的变化曲线，对其积分就可得到如图2(b)所示的熵随温度的变化曲线。在最佳掺杂的情况下，赝能隙基本消失，如果把熵从高温向低温做外插，外插曲线 (图中的红线) 要经过零点。这是态密度或者说状态数守恒的要求，也是所有常规金属超导体所满足的性质。但是对于欠掺杂高温超导体熵，熵从200 K的相对高温的区域做外插并不过零，而是外插到一个负数，表明有很多低能的熵消失了。类比于暗物质暗能量，也可称这个负熵为暗熵。暗熵的存在，当然不是说熵真的消失了，否则就会破坏状态数的守恒条件，而是转移到了比200 K要高得多的能量状态上去了。这是一个我们过去从未见过的物理现象，它意味着发生在低温的低能激发，和非常高温的电子激发是关联在一起的，我们不能简单的认为高能电子对低能物理性质的影响只是重正化一下耦合常数，量子场论的可重正化性假设有可能对高温超导是不适用的。

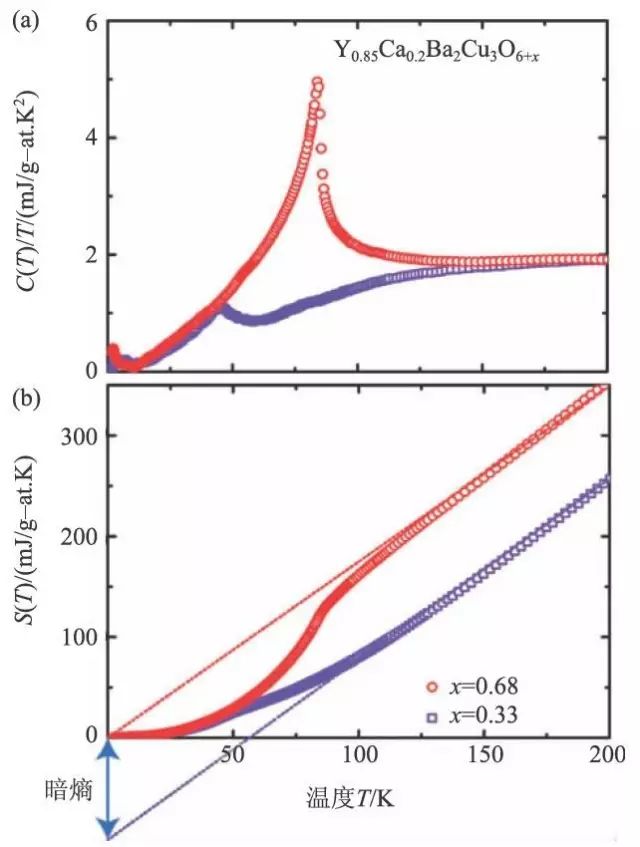
图2 Y0.85Ca0.2Ba2Cu3O6+x超导体的比热(a)和熵(b)随温度的变化曲线

2.3 预配对

在超导体中，存在两个能量尺度。一个是配对电子形成库珀对的能隙Δ ；另一个就是库珀对之间位相的相干能，也就是破坏库珀对之间相位相干所需要的能量，它正比于超导体的超流密度ρs 。

由于存在这两个能量尺度，破坏超导也存在两种不同的途径：一是拆对，也就是通过激发，把库珀对中的两个电子拆散；二是退相干，扰乱库珀对之间的位相，破坏其相干性。对于绝大多数金属超导体，电子配对的能隙远远小于位相相干能， Δ ≪ ρs ，拆对是破坏超导的主要原因，超导温度应正比于超导的能隙Δ 。相反，如果位相相干能远远小于超导的能隙， Δ ≫ ρs ，破坏位相相干比拆对更容易，退相干则变为破坏超导主要原因，超导相变温度应正比于超流密度ρs 。这时，在超导转变温度之上，依然存在库珀对，但库珀对之间的位相涨落太强，无法形成长程的超导位相相干，这就是预配对的物理图像。

在欠掺杂高温超导体中，实验发现超导转变温度近似随超流密度ρs 线性变化，说明在超导相变温度之上超导的位相涨落很强。由于赝能隙出现在同样的温度区间，因此也有人认为赝能隙相就是一个预配对相。但有关超导位相涨落的理论还很不完善，什么是超导位相涨落特有的性质目前并不清楚，更不可能根据这种理论对赝能隙性质做出准确的预言。

最近，Bozovic 等发现，过掺杂的镧锶铜氧超导体的超导转变温度也几乎是随超流密度线性变化的。这个结果不能在朗道费米液体理论的框架下得到合理的解释，说明即使是过掺杂的高温超导体中也存在反常。

2.4 电荷自旋分离

电子带有电荷和自旋两个自由度。在固体中，对应就有电荷和自旋两种不同的元激发。如果相互作用与自旋无关，这两种元激发的能量尺度是一样的。但在高温超导材料中，电荷与自旋激发的特征能量尺度是分开的，被称为电荷自旋分离，这也是高温超导体中普遍存在但没有系统的理论能够刻画的一个现象。

事实上，电荷自旋的分离在没有载流子掺杂的莫特绝缘体中就存在。在莫特绝缘体中，电荷激发存在能隙，而自旋激发是无能隙的，因此在低能极限下，电荷被局域化，呈绝缘性质，而自旋激发可以自由运动，不受约束，与能带绝缘体中情况完全不同。

掺杂后，电荷激发也变得无能隙。但电荷与自旋激发的特征能量尺度还是分开的，因此电荷自旋分离依然存在。这两个能量尺度可分别通过角分辨光电子谱测量电子的单粒子谱函数和能量动量色散关系得到，也可通过输运实验测量电子的纵向和横向弛豫率 (即弛豫时间的倒数) 得到。电子的纵向和横向弛豫率对应的分别是电子电荷和自旋激发的弛豫率。

在最佳掺杂区域附近，实验发现高温超导材料的电阻随温度的变化关系是线性的，不同于在通常金属中观测到的电阻随温度的平方变化的行为。线性电阻也在其他强关联量子材料中观测到，有可能是量子临近涨落导致的，但具体是什么相互作用或散射过程导致这种现象的产生目前并不清楚。根据线性电阻，可以推断纵向弛豫率是温度的线性函数。横向弛豫率可以通过霍尔系数的测量得到。实验发现横向弛豫率是随温度的平方改变的，与纵向弛豫率不一样，说明电荷与自旋的激发是分离的。

03解决高温超导问题的困难之处

高温超导自1986 年发现以来，经过三十多年的研究，我们对它的性质已经有了非常好的了解，但高温超导的机理这个最重要的问题依然没有解决。可以说，高温超导材料是我们研究的最清楚的，但也是最不清楚的一类材料。

高温超导研究中最为清楚的就是超导电子配对的对称性。高温超导电子配对具有d 波对称性，得到了包括光、电、磁、热等大量实验测量的验证和理论研究工作的支持。超导电子配对对称性的确定，为准确定量预言高温超导材料在超导相的物理性质奠定了基础。但仅从超导电子的对称性，并不能唯一确定导致这种电子配对的相互作用是什么。这是因为超导电子配对对称性不仅与相互作用有关，而且还与费米面在动量空间的位置及几何形状有关。相同的配对相互作用，费米面发生变化，配对对称性也可能发生变化。因此，仅从超导配对的对称性并不能确定超导电子配对的机理。

在文献中，通常有一种观点认为，只要实验上观察到同位素效应就证明是电声相互作用导致的超导电子配对。这个观点缺乏理论依据，同位素效应是电声相互作用起作用的必要条件，但不是充分条件。同样，从理论上讲，超导相变温度也不存在一个特殊的不可超越的极限，不能说因为超导相变温度超过了某个温度就不是电声相互作用导致的。2015 年，Eremets 等发现硫化氢在高压下会变成超导体，相变温度可达近200 K。如果他们的实验结果得到最终的证实，那么高压下的硫化氢将是迄今为止发现的相变温度最高的超导体，这种超导体的超导电子配对就极有可能是电声相互作用导致的。

对于铜氧化物高温超导体，目前流行的观点认为超导电子配对主要是由反铁磁的涨落导致的。原因主要有两点：一是高温超导材料中的确观察到了非常强的反铁磁涨落；二是反铁磁相互作用的特征能量尺度比这类材料的德拜温度要高5 倍左右，由此导致的超导能隙比较大，有利于高超导相变温度的出现。但对于反铁磁涨落的理论描述，目前还很不清楚，还无法基于这种理论对超导性质做出比较系统可靠的预言。

高温超导的实验研究在过去的三十多年积累了大量的数据，为高温超导的研究提供了有力的数据支撑。但就高温超导机理研究而言，实验上还给不出具有判断性的测量数据，缺乏一锤定音的结果。

高温超导机理研究的一个重要目标就是要判定是什么相互作用导致了超导的电子配对，也就是准确判断到底是电声相互作用、电子与磁涨落的耦合、还是电子与其他元激发的相互作用导致了电子的超导配对。目前的实验主要是通过对电磁响应函数、热力学量、电子能谱等物理量的测量来研究这个问题，测量结果提供一些关于超导电子配对相互作用的信息，但实验测量的物理量与电子相互作用的关系通常都非常复杂，很难唯一或比较准确地确定到底是哪种相互作用导致了电子的超导配对。

要解决这个问题，必须发展能够直接调节和探测电子与其他元激发相互作用的实验探测手段。如果是电声相互作用驱动的超导电子配对，那么通过调节电声相互作用，在尽可能不扰动其他物理参量的情况下，就可以有效地改变超导相变温度。反之，如果无论怎样改变电声相互作用，超导相变温度都没有明显变化，也就证明超导电子配对不是来自于电声相互作用。同样，要判断铜氧化物高温超导电子配对与磁涨落的关系，最好方法也是直接调节电子与磁涨落的相互作用。通过掺杂、改变压力等手段也可以改变超导相变温度，但这些方法往往把很多参数都改变了，很难知道哪个量的改变起了主要作用。直接调节和探测电子与其他元激发相互作用就是为了避免这种盲目性。这种新的探测技术的发展，不仅对超导研究具有重要的意义，而且对其他功能材料或器件的开发和研究也会起到极大的推动作用。

理论上讲，高温超导之所以难研究，是因为高温超导的特征能量尺度比普遍金属的特征能量尺度要小两个数量级。表征金属的一个特征能量尺度就是电子的费米能，大概在一个电子伏特的量级，转换成温度，大约是一万多度。也就是说，对于普通金属，我们只要在一个电子伏特的能量分辨率上，把相互作用作为微扰，就可以对它的性质做非常好的预测。高温超导的一个特征能量尺度，就是超导的相变温度，大约在100 K左右，比金属的电子费米能小两个量级。因此，要理解高温超导的性质，我们需要的能量分辨尺度也要高两个量级。已有的固体电子论还达不到这么高的能量分辨的要求。而且，这个能量尺度和电子与其他元激发的相互作用同量级，微扰论不再适用，没有成熟的非微扰量子场论方法可用。

解决这个问题的主要思路有两个。一是基于实验结果的唯象分析，发展非微扰场论方法和理论。这方面包括共振价键理论、U(1) 规范理论、位相及反铁磁涨落理论等，但这些理论都不够系统，缺乏预言能力；二是发展新的多体量子计算方法，通过对哈伯德 (Hubbard) 模型等高温超导基本模型的研究，探索和发现高温超导材料中出现的各种反常现象的物理根源，为解决高温超导的机理问题提供科学依据。

高温超导材料的电子结构非常复杂，要把所有的因素都包括进来研究从现在来看是不现实的。因此模型的研究在强关联量子问题的研究中占据着重要的地位，这方面取得进展的可能性也更大一些。相变问题的研究，就是通过对极端简化的二维伊辛模型的求解取得突破的。

高温超导研究推动了多体量子计算方法的发展，同时这方面的进展，也促进了高温超导的理论与实验研究。密度矩阵重正化群、量子蒙特卡罗、动力学平均场理论以及严格对角化方法相对比较成熟一些，但这些方法在处理二维非半满的电子系统或有阻锉的量子自旋系统存在一些局限性，还不能用于系统解决高温超导材料中的问题。张量重正化群是近年来发展的一种新的多体量子计算方法，这种方法没有量子蒙特卡罗方法遇到的负符号问题，是一种应用范围更广的计算方法，已经在量子自旋问题的研究发挥了其他方法无法替代的作用，也为更广泛解决强关联量子计算问题带来了希望。

04展望

高温超导机理到目前为止，还是一个没有解决的问题。但高温超导的研究，促进了角分辨光电子谱、扫描隧道电子谱等实验技术的发展，也激发并推动了新的多体量子理论、以及包括密度矩阵及张量重正化群在内的多体计算方法的发展。同时，高温超导的研究也对凝聚态及材料物理的其他领域的发展起到了带动作用，引发并带动了量子临界性、量子自旋液体、庞磁阻、多铁性等问题的研究。

解决高温超导机理问题，可以为寻找新的高温超导体，特别是室温超导体提供理论依据；也对提高高温超导材料的性能，扩大其应用领域具有指导意义。但这不是高温超导研究的唯一，甚至不是最主要的目的。高温超导问题是物理学的一个基本问题，它揭示了大量新的多体量子现象，这些现象不能在已有的多体量子场论框架下得到解释。因此，解决高温超导机理问题，就必须建立新的多体量子理论体系。这个理论的建立，毫无疑问将对全面系统解决强关联量子问题起到关键的作用，同时也将对量子场论及物理学的其他领域的发展产生深远的影响。而高温超导正是提供了启发并检验这个新的量子理论的一个脚本。

致谢 感谢孙力玲、周兴江、张广铭、王楠林和李建新5位老师对文章提出宝贵的修改意见。

参考文献

[1] Kotliar G，Liu J. Phys. Rev. B，1988，38：R5142[2] Hardy W N，Bonn D A，Morgan D C et al. Phys. Rev. Lett.，1993， 70：3999[3] de Boer J H，Verwey E J W. Proc. Phys. Soc.，1937，49：59[4] Mott N，Peierls R. Proc. Phys. Soc.，1937，49：72[5] Castellani C，Di Castro C，Feinberg D et al. Phys. Rev. Lett.， 1979，43：1957[6] Alloul H，Ohno T，Mendels P. Phys. Rev. Lett.，1989，63：1700 

[7] Loram J W，Mirza K A，Cooper J R. Phys. Rev. Lett.，1993，71：1740 

[8] Loram J W，Mirza K A，Cooper J R. Physica C，1997，282：1405

[9] Uemura Y J et al. Phys. Rev. Lett.，1989，62：2317

[10] Emery V J，Kivelson S A. Nature，1995，374：434

[11] Božović I，He X，Wu J et al. Nature，2016，536：309

[12] Tsuei C C，Kirtley J R. Rev. Mod. Phys.，2000，72：969[13] Wheatley J M，Xiang T. Solid State Commun.，1993，88：593[14] Drozdov A P，Eremets M I，Troyan I Aet al. Nature，2015，525：73[15] Anderson P W. Science，1987，235：1196[16] Jiang H C，Weng Z Y，Xiang T. Phys. Rev. Lett.，2008，101：090603；[17] Xie Z Y，Jiang H C，Chen Q N et al. Phys. Rev. Lett.， 2009，103：160601

本文经授权转载自微信公众号“中国物理学会期刊网”。