刘谦在今年春晚的第一个魔术表演中隐含着数学问题，但鲜见科普文章提及。实际上，这里的问题或许更受数学家们关注。

撰文 | 南山莲子

刘谦在春晚表演的第二个“魔术”，其实就是数学原理的应用。相关的解释已有不少。这类利用数学原理进行表演的扑克游戏有不少。如袁亚湘院士就曾在央视表演过一些数学扑克魔术。看刘谦春晚魔术不过瘾？院士给您讲解数学魔术

刘谦在今年春晚的第一个魔术表演中也有数学现象。但鲜见有普及文章提及。实际上，其中的数学问题或许更受数学家们关注。

让我们回顾下。刘谦在第一个魔术表演开始时夸张地说，

这位先生和这位小姐，从三天前就开始洗牌，洗到现在还停不下来。让我来反问下，您打算洗到什么时候？满意了吗？

随后刘谦表演了短时间内洗出四条龙（假设一副扑克牌有52张），而且最后一条龙还暗合现场时刻。一副52张扑克牌的扑克有52!种排法。所以得到四条龙的特定排法的概率为这是一个极其微小的概率。数学家李特伍尔德曾如此定义奇迹：“奇迹就是发生的概率小于一百万分之的概率的事件。”在这个意义上，春晚观众确实如刘谦所说，见证了奇迹。虽然搞笑，但不妨启发人们思考如下重要问题：

如何洗牌？洗多久能洗好？哪种洗牌方法需要时间最少？

完美洗牌

有赌博必然有洗牌。因而也产生了很多洗牌的方法。下面仅考虑一种所谓的完美洗牌。这是一种交错洗牌法。又分为内洗法和外洗法。

首先，将一副牌分成相等的两摞。外洗法使牌交替放置成如下顺序：第一摞的第一张牌、第二摞的第一张牌、第一摞的第二张牌、第二摞的第二张牌，……。内洗法：先交换两摞牌的位置，再按外洗法的方法排列牌。示例如下：假设你的牌组有12张牌，由上到下如下排列：

A，2，3，4，5，6，7，8，9，J，Q从中间将其分成两摞：第一摞是A，2，3，4，5，6；第二摞是7，8，9，J，Q所谓外洗法就是把牌按如下顺序排列牌：A，7， 2， 8， 3，9，4，10， 5， J， 6，Q而内洗法是先把这两摞牌交换，其后再按外洗法的方式交错洗牌，得牌序如下：7，A， 8， 2，9， 3，10， 4，J， 5， Q， 6

洗牌群

将一副扑克牌的52张牌分别标记为这种标记方法是不记录牌的点数和花色，相当于仅仅记录各张牌的位置，只不过将最上面的牌标号为0，这是为了后面的数学处理（模运算）方便。一次洗牌就是这52个数字的排列。前面已经介绍，总的排列数为。全体排列组成一个排列群。如果仅考虑一副只有6张牌的牌组。6张牌共有种排列方法。但我们可以只考虑由外洗、内洗所能得到的牌的排列方式。先只考虑外洗法。可以得到的排列如下：

1. 分成两摞：

外洗可得：

1. 再分成两摞，可得

外洗可得：

1. 再分成两摞，可得

外洗可得：

1. 再分成两摞，可得

外洗可得：由此可见，经过4次外洗，可以回到原先的顺序。还可知道，由外洗可得4个排列：类似地，也可以考虑内洗，经过有限次内洗，也可以回到原先的顺序。

还可以考虑全体内洗、外洗所得的排列，如此得到的排列的全体，被称为完美洗牌群。完美洗牌群是全体排列组成的一个群的子群。一个最简单情况是两张牌的情形。设有0,1两张票。全体排列如下：（）设原始顺序为，则外洗只能得到它自己。如果考虑内洗，则所得完美洗牌群就是全体排列组成的群。考虑完美洗牌群的大小是一个有趣的问题。如果只有6张牌，总共有种排法。但完美洗牌群只有24种排法。

类似地，若一共有10张牌，则洗牌群共有1920种排列。若一共有14张牌，则洗牌群共有 320,000中排列。若一共有26张牌，则洗牌群共有超过25万亿种排列。上述例子暗示，如果增加牌的张数，则洗牌群的数目按指数增加。然而，如果牌的张数是2的指数次，则洗牌群的数目按指数减少。例如，若牌的张数为张，则洗牌群的大小为。若牌的张数为张，则洗牌群的大小为。

洗多少次

从前面一副牌是6张牌的例子可以看出，若只用外洗法，则只要4次就可以复原。那么，对一副52张牌的扑克牌，用外洗法，多少次后就复原了？设52张牌排列如下：分成两堆，上面那堆为下面那堆为交错洗牌得可见，第一堆中原来位置在处的牌被放到新堆的处。例如，2在第一次外洗后，被放到4位置。类似地，位置在（）处的元素在新的堆中排在位置处。利用模算法，一次外洗将换到处；两次外洗将换到;等等。从而，若次外洗可以将换到处，则应有求解上述方程，可知这是因为我们有下表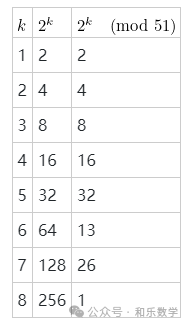也就是说，外洗8次相当于什么也没做。洗牌还有很多数学问题，上面仅仅简单介绍了一点基础。有兴趣的网友可以进一步阅读相关资料。

本文经授权转载自微信公众号“和乐数学”。