代数学是伴随着早期文明的产生而产生的，它是最早的、有组织的智力活动之一。代数化是20世纪数学发展的一个重要特征和有效引擎，将代数的思想和方法渗透到其他领域的研究中，所呈现出的“交叉融合”的数学倾向是20世纪数学发展的特色之一。

撰文 | 闫焱（华北理工大学理学院教授）、邓明立（河北师范大学数学科学学院教授）如果要对代数学的历史寻本挖源，它几乎可以和人类的文明史相媲美。著名数学大师范·德·瓦尔登（B. L. van der Waerden, 1903-1996）认为，在美索不达米亚、埃及、中国以及印度的古代文明之前，就存在着一种文明，这种文明是大部分早期数学的源泉[1]。代数学是伴随着早期文明的产生而产生的，它是最早的、有组织的智力活动之一。代数学和美术、音乐以及宗教一样，也是一项基本的、自然的人类活动。

代数化趋势的形成

代数学的历史可以追溯到什么时候呢？最早的代数起源于度量、计时和土地测量等实际问题。据记载，在公元前3000年左右，埃及和巴比伦的文明中就产生了以实用为目的的数学。在数学这条困难重重的道路上，古埃及人大大推动了人类的进步，他们创造了最早的方程。古巴比伦人则在数学道路上走得更远，为了求解一些特殊形式的方程，他们创造了用特殊符号代表未知量的方法，这些都是代数早期的初始形态。在数学史上古希腊人是至高无上的，公元前4世纪古希腊时期不仅诞生了真正的数学，从哲学到民主制，应有尽有，这一时期的数学、社会及文化共荣发展。

古希腊数学家丢番图（Diophantus，约246-330）是代数学重要的创始人之一。在13卷巨著《算术》中，丢番图发明了用字母表示未知数的方法，并开始解答含有若干未知数的方程，为此还发明了能简化解题过程的运算定律[2]。印度文明可以追溯到公元前2000年，但是据记载，他们在公元前800年以前是没有数学的。古印度代数学主要被用于天文、利息与折扣计算、合股分红、财产划分等，在代数学的表达上采用缩写文字和一些记号来描述运算，但是这一时期符号的使用比丢番图的缩写代数用途更加广泛。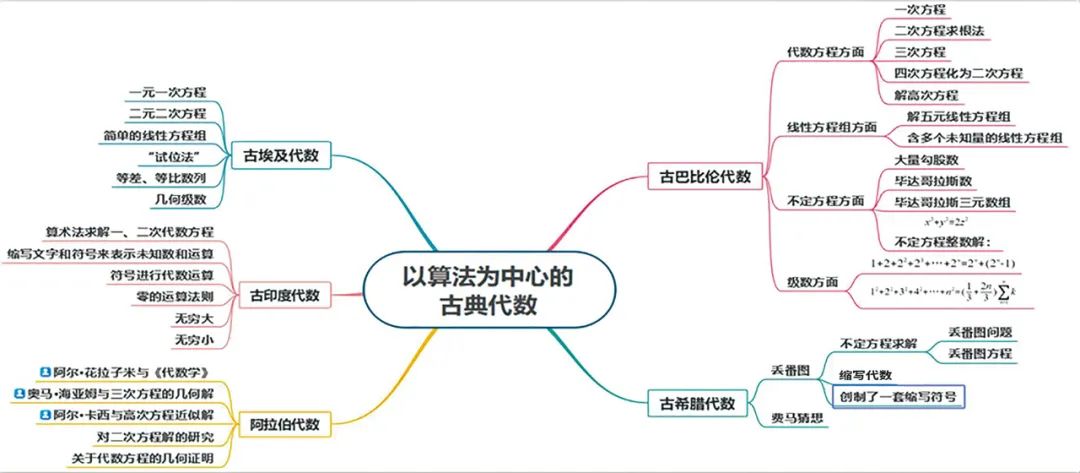以算法为中心的古典代数学花拉子米“代数”一词可以追溯到公元9世纪阿拉伯数学家、天文学家花拉子米（Al-Khwārizmī，约780-约850）的著作《还原与对消的科学》(al-jabr wal muqābala) 中的“al-jabr”，该词的本意为“还原”，即在方程中将负项移动到方程的另一端“还原”为正项。“代数”这个词并没有被翻译成拉丁语，人们直接用它来表示这个尚未命名的新数学分支，该词后来在英语中的用法与代数一词的用法相同，后被简译为“algebra”。1859年中国数学家李善兰（1811-1882）与英国汉学家伟烈亚力（A. Wylie, 1815-1887）合作翻译了德·摩根(A. de Morgan, 1806-1871)的《代数学基础》(The Elements of Algebra)，首次将“algebra”译成“代数”，由此代数作为新数学学科被引入中国，开启了西方代数学在中国进行传播的新纪元。

从5世纪到11世纪，代数学的发展在整个中世纪处于凝滞状态。12世纪在数学史上是翻译者的世纪，当阿拉伯和希腊的一系列著作被陆续翻译、传播到欧洲以后，欧洲数学开始复苏。13世纪前期，欧洲各地兴建了一些历史上著名的大学，代数学在这些大学中得到了重视和发展。在14世纪的文艺复兴时期，数学像美术、音乐、文化以及科学一样在欧洲繁荣了起来，并且发生了根本性的变化，据记载这种新的数学开始于代数学中的发现。意大利数学家在求代数方程的精确解方面取得了重大的进步，他们的算法已经远远超出了自美索不达米亚时代起任何解方程的算法。此外，意大利数学还出现了另一种趋势，即用代数学去解决科学中的问题。意大利科学家、数学家及发明家伽利略的工作最能说明科学家已经开始注重用代数学作为表达自己思想的语言。伽利略的名著之一《关于两门新科学的对话》（Dialogues Concerning Two New Sciences）中遍布着代数学思想[1]，但是这并不是一部代数学著作，而是一部关于科学的著作，伽利略在这部著作中利用代数函数的文字形式表述了自己的科学观点。伽利略的代数学方法告别了过去，因为在以往的一千多年来，几何学一直都是进行科学探索的语言，科学家与数学家们常常使用直尺和圆规来表达自己的思想。尽管伽利略通过代数函数描述了物体的物理性质，遗憾的是，他没有使用便捷的代数符号来表述这些思想。

但是16世纪代数学的重要进展已经成为数学最显著的成就。以费罗（S. D. Ferro, 1465-1526）、塔尔塔利亚（N. Tartaglia, 1499-1557）、卡尔达诺（G. Cardano, 1501-1576）、费拉里（F. Lodovico, 1522-1565，人们习惯称其名）等为代表的数学家（他们都略早于伽利略）发现三次和四次方程的代数解为主要标志，大大推动了代数方程的研究和发展。16世纪末到17世纪，产生了近代数学的三大基础学科之一的符号代数学。符号代数学（或字母代数学）的产生并没有改变代数的算法本性，并由此派生了两类相关的新问题[2]：计算对象以及计算法则。韦达（F. Viète, 1540-1603）是第一个系统地引入代数符号的数学家，依照今天的代数视角，这个符号体系不但复杂而且效果甚微。

随后，笛卡儿改进了韦达的符号体系，比如在语言上笛卡儿使用的是易懂的法兰西口语，在形式上去掉了许多不必要的限定条件。1628年，笛卡儿将前人的几何分析方法同近代人的代数方法相结合，从而形成了统一的普遍数学（构造出普遍方法来解决科学问题，特别是数学问题，对此笛卡儿称之为普遍数学），从而完成了符号代数学的建立，这套符号体系被广泛用于解决各个领域中的实际问题，如土木工程、军事工程、天文学、航海学、会计学等。

古典代数学大多使用的是语言描述，现在使用的代数符号是在17世纪沿用下来的。在数学史上，17世纪是一个引人注目的富于开创性的世纪，世界数学进入了近代数学时期，这一时期数学发展的特征是代数化趋势明显。最为典型的就是笛卡儿把变量解释成数量（即线段的长度），使他首创了将代数方法作为研究几何学的一种工具，建立了解析几何学，实现了代数与几何方法的统一，并将此方法付诸解决科学问题。代数学的发展史是伴随着漫长的符号化进程的：从数字及其表示的符号化→运算的符号化→关系的符号化→各类量的系数符号化→更一般对象的符号化。在这种背景下，笛卡儿和莱布尼茨产生了逻辑符号化的思想，这种思想后来发展成符号逻辑，成为数理逻辑（重要的数学基础之一）的前身。事实上，符号化是使问题代数化至关重要的一步，它使得初等几何学问题变得代数化、形式化，从而为程序化以及机械化证明奠定了基础。在这种符号化的演变过程中，代数学作为一种符号语言，从字符体系的发明开始，不仅在数学中赢得了突出的地位，也促使数学家在表述自己思想的同时，不断持续提升对符号系统的思维意识。

18世纪分析学在一定程度上推动了代数学的进展，在方程演算不断发展的过程中，数值计算（或近似计算）以及方程理论问题逐渐成了代数学发展的新倾向和主流。尽管如此，符号代数学的产生并没有改变代数的算法本性，但由此派生了两类相关的新问题：计算对象以及计算法则。大约在1840年前后，代数学发展成为对任意对象进行运算操作的一门科学。

计算对象以及计算法则又得到了新的发展，计算对象进一步扩大，特别是行列式、矩阵、置换、变换等均可以成为运算的对象，只是它们的计算法则不一定服从数的运算法则。计算法则更加系统，比如幂等律、德·摩根律等新规则的确立。此外，代数符号化促使了结构形式化的发展，这使得从1840年前后到1920年前后，在抽象群理论、交换环论、交换代数理论、域论、结合代数及非结合代数理论以及李群理论的发展过程中，形式地推广促进了不同问题的解法统一成共同的算法，这些都推动着代数学逐渐走向了结构数学研究的道路。

近世代数学——研究抽象代数结构的一门结构数学

19世纪数学家发现对于五次、六次乃至次数更高的方程找不到求根公式，在这种情况下，数学家希望创造出另一种代数，转向一个新领域。这一时期，整个代数学由于群及域的观念而使其自身发生了根本的改变，这种远离古典代数学的异端在最初并不被世人所接受，经过了四五十年的发展之后，人们才开始意识到数学的对象除了“数”与“形”，还有“群”这类抽象的对象。19世纪中后期，诸如群一样的抽象对象层出不穷，代数学迎来了新的局面，这为代数结构观念在20世纪的发展奠定了基础。

19世纪末，当抽象群可以概括所有具体群的共同性质，抽象群概念随即诞生，并且可以很自然地把许多具体群论的结果都推广到抽象群中。由于群概念的日趋成熟且涵盖了当时大部分的数学，因此一大批数学家尝试以群的观念来统一数学。另一方面，在集合论的刺激下，产生了探索数学基础的运动热潮，20世纪初形成了三大“数学哲学”学派：直觉主义学派，其代表人物是布劳威尔（L. E. J. Brouwer，1881-1966）；形式主义学派，其代表人物是希尔伯特；逻辑主义学派，其代表人物是罗素。三个学派坚持用各自的主张统一数学，尽管都有成就，但是均以失败告终。伽罗瓦数学史上，近世代数学思想的发展经历了由“戴德金（J. W. R. Dedekind, 1831—1916）→希尔伯特→诺特→范·德·瓦尔登”的过程。戴德金作为库默尔（E. E. Kummer, 1810-1893）的得意门生，他在库默尔理想数的基础上，提出了理想概念（复整数的集合），建立了理想理论，实现了从数到集合的推广。戴德金的代数学思想影响广泛，希尔伯特、诺特等大批数学家都传承了他的数学思想。特别是诺特，她曾参与编辑出版了戴德金的三卷全集[2]，这让她对戴德金的工作有了深入的思考，并用自己的思想和逻辑体系呈现并凝练出了惊人的近世代数成果。诺特的抽象代数系统研究始于理想理论，特别是她对交换环论的工作使之成为代数学的重要研究领域，并且在数学中产生了强大的内交叉效应，促使了很多其他数学分支的发展。

1930-1931年，得到诺特真传的范·德·瓦尔登出版了《近世代数学》（Moderne Algebra），确定了代数结构化的思想形成，成为数学代数化趋势的思想源泉，标志着抽象代数学正式诞生[3]，这部书也被世人公认为是抽象代数学发展过程中的一个里程碑。在随后的几十年中，这部著作为代数学的写法建立了一个类似范·德·瓦尔登的范式，它以结构为指向的“近世代数学”从根本上改变了代数学的整个面貌。1950年代第四版起改名为《代数学》（Algebra），对此范·德·瓦尔登解释说，在1930年还可以称为是近代的代数学，在今天，这就是代数学了。

19世纪群论的诞生，驱动着代数学向抽象代数方向发展，数学对象及方法得到了大范围的推广。在这一时期代数学的发展方向产生了几次拐点，比如方程数值解法和近似解法的发展、方程论及置换群论的发展、抽象群及表示论的产生、型论及不变式论的发展、消元法技术的产生、交换代数理论的产生、四元数及其各种推广、非结合代数的产生等。

19世纪数学的多样性在代数学的演变中得到了淋漓尽致的彰显，伴随着代数学的发展，抽象化为20世纪结构数学的诞生植入了强大的动力，在数学基础与数理逻辑的研究中，集合的观念、公理化方法和结构的意识愈演愈烈。20世纪20年代末至30年代初，抽象代数逐渐成为代数学的主流，其研究的对象是满足若干条件、具有代数运算的集合。

在这一时期，“代数”一词有两种含义：一是作为一个数学分支；二是作为一种代数结构，如前面所提到的群、环、域，它们都是由一些公理来进行定义的。从结构的角度研究代数是20世纪代数学研究发展的一个趋势，抽象代数讨论代数结构，其中最基本的对象是群、环、域，其他对象都是这三个对象衍生出来的[4]。在20世纪的前几十年里，很多数学家都在他们各自认知的领域里，深入挖掘是否存在群、环、域这些结构，以便在更抽象的结构层次上考虑问题。群作为最纯粹的代数对象，具有应用性广、抽象度高的特点。环和域虽然具有较为复杂的代数结构，但是它们拥有极为明显的数的背景，而且它们的发展完全与数的推广密切相关，因此在数与多项式的背景下，理解环和域是比较形象的。诸如环、域和模等许多代数结构都可以看成是在群的基础上衍生出来的，由此可见在代数中群具有最基本的重要地位。

1930年代，“新数学基础”运动席卷数学界，布尔巴基学派就是在这种背景下产生并初显他们所提倡的结构主义运动端倪的，结构数学由此应运而生。与经典数学的数与形不同，结构数学关注的是对象的结构。数学结构主要是一些对象的集合，着重考虑的是它们之间的关系，对于抽象的集合，元素和元素之间除了它们有共同隶属于该集合这种共性之外，一旦元素之间存在一些特殊的关系，结构也就产生了。定义结构的方式一般是这样引入的：首先，需要阐明一系列法则，然后数学家对服从这些法则的对象进行研究，这些法则用数学术语来说叫作公理。在某一个学科体系内建立公理具有一些显著的好处：第一，这些法则使得研究范围清晰化；第二，人们通过事先约定法则，可以确保在讨论数学对象时所有人头脑中想的是同样的对象;第三，可以依法则为基础进行逻辑推导，从而得出一些起初从法则本身没有预见到的事实。

代数学的渗透与应用

在集合化和公理化浪潮的作用下产生了很多的抽象结构，由此引发众多数学研究者投入到创建新方法、发展新理论、实践新交叉或者新应用的研究中。众多数学家喜欢追求清晰的数学结构，在这一过程中经常会流露出一种常见的数学哲学思维：抛开多余的信息，抓住问题的本质。数学推理的魅力常在于找到一个框架，在其中将试图证明的结果变得几近明显，数学的创造力主要在于找到这样一个框架。正如数学史的发展长河经过上百年的洗礼，数论、代数、几何及分析四个互不相干的数学领域逐步形成了一种共同的代数结构——交换代数。代数数论、代数几何和不变量理论可以视为是交换代数的三大起源。反过来，交换代数也通过交叉渗透去影响这些领域的发展。

20世纪的数学发展中一个重要趋势是不同学科互相渗透和由此发生的统一，其中诺特所开创的抽象代数学以及她的抽象思想方法不仅奠定了代数学的未来发展，也促使了整个数学“代数化”趋势的产生，特别是交换环理论的交叉应用。代数数论的研究也从早期侧重算术方面的研究，转移到侧重代数方面的研究。历史上，代数数论中的唯一分解定理、理想、模等为交换代数提供了早期的框架。再有，作为19世纪最伟大的数学创造之一的代数几何，该理论体系中最原始的公共零点以希尔伯特不变式论的形式，构建了诺特环的基础理论。反过来，交换代数为代数几何提供了有力的工具，两者之间的界限现在已经逐步消失，并融入数学的前沿领域中[3]。

还有，19世纪的代数函数论曾是数学研究的核心地带，许多数学家将代数函数论作为代数几何的超越理论加以论述，这样代数函数论很自然地被融入代数几何并成为其中的组成部分。由此从几何的角度，代数函数论被纳入代数几何学范畴。到了20世纪中叶，代数函数论同一般域上的代数曲线论被纳入交换代数范畴，这是典型代数化的作用影响结果。回顾展望这些与交换代数相融合的理论，不禁感叹这位伟大的“抽象代数之母”——诺特，是她赋予了抽象代数这门学科旺盛的生命力，并在很多学科领域植入了抽象代数这颗强大的种子。诺特多学科交叉融合是数学创新的重要来源之一，在数学中很难有哪个数学分支能够与代数学的历史变迁同日而语，代数学既承载了数学发展史中的经典厚重，又势不可挡地展现了交叉融合背景下不容忽视的强大力量，使其思想和方法不断渗入许多学科领域之中。诺贝尔物理学奖获得者、美籍匈牙利理论物理学家维格纳（E. Wigner, 1902-1995）曾在他1960年的里程碑式的论文《数学在自然科学中不可思议的有效性》（The Unreasonable Effectiveness of Mathematics in the Natural Sciences）中提到[1]：

“这是一种奇迹，代数学的不可思议的有效性随处可见。”

20世纪以来，不同分支领域的数学思想与方法汇集碰撞、成果交流，代数学在这一过程中成了交叉融合发展理念下的有效引擎，它通过与其他学科的互通互融，算子代数、代数拓扑、代数组合等新学科如雨后春笋般破土而出。20世纪伟大的德国数学家外尔在《半个世纪的数学》（A Half Century of Mathematics）中曾写道：

“群的概念是由年轻的法国天才伽罗瓦引进的，现在已经扩散到整个数学中，没有群就不能理解现代数学。”

由于群结构具有普适的一般性和外延的张力性，在派生数学新领域、新内容的过程中，群方法成为极具创造性的思维模式，代数学成了20世纪融合发展理念下的有效引擎。代数学通过与其他学科的交叉融合，代数拓扑、代数组合等新学科如雨后春笋破土而出。正是在这种不同学科间的交叉融合中，现代数学仿佛被注射了一支活力剂，蓬勃发展，方兴未艾。从群论的观点来研究组合数学，这为组合数学注入了新的活力，亦为代数组合这门学科找到了适合的生长点。国际数学界常将代数组合（algebraic combinatorics）视为“组合对象的表示理论”或“没有群的群论”。代数组合是组合数学与抽象代数两门学科的一个重要分支，除了可以利用代数方法或结论研究组合问题，也可以利用组合方法或结论研究代数问题。代数组合的特色魅力就在于通过数学结构，本质上彰显了在数学统一性的趋势下表现出来的代数学的渗透与应用。

代数组合的起源可以追溯到数学领域的不同分支，其中一个重要起源可以追溯到群论中舒尔（I. Schur, 1875-1941）在1933年关于舒尔环的工作。最初舒尔环是用来研究具有正规子群的本原置换群的，其中大部分的结论后来被发现也适用于具有正规群作用的本原结合方案（代数组合中的一个核心概念和重要的研究方向）。

此外，代数组合这门学科的研究历史可以与群的特征理论媲美，包括弗罗贝尼乌斯（F. G. Frobenius, 1849-1917）、舒尔和伯恩赛德（W. Burnside, 1852-1927）的研究理论。特别是20世纪30-60年代，群论专家维兰德（H. Wielandt, 1910-2001）和希格曼（D. G. Higman, 1928-2006）等人关于有限置换群的工作（置换群的中心化子环）[5-7]，由此打开了新的局面，促进了代数组合领域的发展。代数组合与有限群论、编码、图论、组合设计有着密切的联系，在调和分析、代数几何、表示论和数学物理方程中发挥着积极的作用，并且在化学、信息论、计算机科学、工程技术等领域具有重要的工具价值。自代数组合被系统研究以来，许多群论的概念和性质被发现可以推广到结合方案上来，例如：子群、正规化子、有限群的幂零性、西罗定理等。不仅是群中的概念和性质，类似有限群的表示理论，结合方案的表示理论也是研究结合方案数学结构的有效途径之一。这些信息都揭示出一个强烈的信号，在代数组合中看似没有群的结构，但是其学科体系中却蕴含着强大的群论思想和“没有群的群论结构”。“代数组合”一词首先是坂内英一（E. Bannai，1946-）于1979年在日本著名刊物《数学》（Sugaku）上发表的《代数组合论》(代数的組合せ論) 这篇评论性文章中提出的[8]，由此宣告了这门学科的诞生。坂内英一一贯主张以纯粹数学的观点来研究组合学，坚持用群论的视角为组合学的研究开创新的思路和方法[9]，从而建立起“代数思维”与“代数组合中思维实践”之间的关系思考，这正是20世纪这个统一的时代所彰显出来的一种特色趋势——“代数学无处不在”。

回望历史来路，汲取历史智慧，代数学的能量是巨大的。代数学不仅是集合、符号和思维的语言，更是贯穿在科学中的工具。正如数学已经成为科学的语言，代数学通过一代代数学家们的踔厉奋发，笃行不怠，俨然成为数学的流行语言，并实现了将许多种类各异的、高度数学化的学科进行代数化处理。在人类思考和探索代数学发展的历程中，每当所有的代数难题被攻克或者即将被完成的时候，一些全新的问题、学科分支和新思想便会出乎意料地浮出水面，使得人们重新思考之前的知识积累并加以拓展延伸。代数学正是在这样的历史进程中，逐渐彰显出其巨大的能量，成了很多现代数学乃至科学与工程研究中必不可少的组成部分。

[本文相关研究得到国家自然科学基金(12171137)的资助。]

参考文献

[1] 塔巴克. 代数学: 集合、符号和思维的语言. 邓明立, 胡俊美 译.商务印书馆, 2007: 71-87.[2] 胡作玄. 近代数学史. 济南: 山东教育出版社, 2006: 383-385, 630-631.[3] 胡作玄, 邓明立. 20 世纪数学思想. 济南: 山东教育出版社, 1999: 106-117.[4] 邓明立, 王涛. 历史与结构观点下的群论. 北京: 科学出版社, 2016: 92-106.[5] Higman D G . Finite permutation groups of rank 3. Mathematische Zeitschrift, 1964, 86(2): 145-156.[6] Wielandt H. Finite Permutation Groups. New York: Academic Press, 1964: 39-40.[7] Higman D G . Intersection matrices for finite permutation groups. Journal of Algebra, 1967, 6(1): 22-42.[8] Bannai E. Algebraic Combinatorics. Sugaku, 1979, 31: 126-143.[9] Bannai E. Combinatorics regarded as pure mathematics: the aims of algebraic combinatorics. Sugaku, 2010, 62(4): 433-452; 作为纯粹数学的组合理论——代数组合的目标. 高锁刚, 马建敏, 张跃辉 译. 数学译林, 2011, 30(4): 312-325.

本文经授权转载自微信公众号“科学杂志1915”，刊载于2024年第76卷第1期《科学》杂志（P29-P34）。