关于黑洞内部的理论探索一直是物理学研究的重要方向。其中一个难以回答的问题即是奇点是否真正存在。尽管彭罗斯和霍金基于经典引力得到了奇点定理，证实了黑洞的奇异性。但奇点的定义不仅仅只有一种，为了探讨黑洞理论的这一核心问题，近期黑洞研究先驱克尔（Roy Kerr）发文表示——奇点不存在。他为什么会得出这个结论？

撰文 | 安宇森（南京航空航天大学物理学院）

仰望宇宙，瑰丽的星空令人神往，但美丽的同时往往也蕴藏着危险，其中最危险神秘的区域莫过于黑洞。

爱因斯坦1915年提出的广义相对论革新了人们的时空观念。广义相对论的提出标志着，时空并不是一成不变的舞台，而是会因舞台上的观众——时空中的物质——而扭曲，这一作用可以通过求解运动方程（即爱因斯坦方程）进行刻画。一般来说，爱因斯坦方程是极难求解的，但是物理学家总可以找到各种具有良好对称性的情况，以此作为理想模型来开展研究。1916年，史瓦西（Karl Schwarzschild）在一战的战壕中就得到著名的、以他名字命名的解，称为史瓦西度规：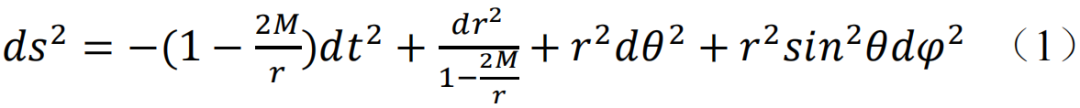
史瓦西度规既可以作为恒星外部的时空解，也可以作为一个球对称黑洞解。观察这个度规，可以明显地看出存在两个特殊的位置，r=2M和r=0，在这两个位置处，度规（1）会发散。对于这两个发散的理解困扰了物理学家很多年。人们最终发现，这两个发散位置实际上对应黑洞最重要的两个特征：事件视界和奇点。对它们的理解，是黑洞物理研究最重要的组成部分。

在介绍黑洞这两个特征之前，我们先来回顾一下黑洞这一概念的形成。20世纪30年代，奥本海默（J. Robert Oppenheimer）和钱德拉塞卡（Subrahmanyan Chandrasekhar）等人对恒星燃尽后的引力塌缩问题进行了深入思考，他们计算发现，当星体质量足够大的时候，理论上并不存在足够的排斥力可以阻碍引力塌缩。因此他们大胆预言引力塌缩不会停止，最终恒星会变得极其致密，进而使得周围的时空高度扭曲，形成黑洞。这一观点在当时受到了诸多质疑，更多人相信，这一预测或许只是因为理论模型的过度简化所致，现实中会存在某种人们还未理解的机制使得塌缩停止，因此黑洞并不是真实的物理实在。

直至今日，关于引力塌缩末期的物理还未得到彻底理解，引力塌缩最终得到的奇点问题仍然困惑着物理学家。然而，对于黑洞的存在，已在当前的引力波观测中得到了很强的证据。不仅如此，前几年人们还拍摄了黑洞的照片。这些进展无不揭示着，我们的宇宙中真的存在这样一个神秘的天体。

图1 第一张黑洞照片丨图源：Event Horizon Telescope Collaboration

黑洞视界

我们首先来介绍黑洞的两个重要特征之一——事件视界。以史瓦西黑洞为例，对于事件视界，即史瓦西解中r=2M的位置，人们发现度规解中看上去会出现发散，仅仅是由于我们选择坐标的问题。如果我们不选择t, r, θ, φ这一坐标，在其他特殊坐标系下发散便不会出现。

视界的物理特征是由于时空高度扭曲而出现的时空坐标互换。可以很容易地看出，当穿过事件视界，即r＞2M从r＜2M到的时候，原本外部的时间坐标t到视界内部会变为空间坐标，原本的径向空间方向r则会变为时间方向，这一特点是黑洞的本质特点。即使黑洞的外部是不随时间变化的静态时空，黑洞内部也会因为时空坐标的互换不再具有静态性质。

视界的另一物理特征是，处在视界内部的光线，无论是向内还是向外发射的，最终都会汇聚。因此没有任何物质进入黑洞后可以逃脱，就连光也无法幸免。它就像一只饕餮，贪婪地吞噬着周围的一切，这也是黑洞名字的由来。

以上讨论是基于史瓦西解来认识黑洞视界和黑洞内部的物理。在史瓦西黑洞出现不久，人们通过假设黑洞外面具有电磁场，构造了带电球对称黑洞，即R-N黑洞。很长一段时间内，求解爱因斯坦场方程都需要球对称性的帮助。重要的进展发生于1963年，这一年克尔（Roy Kerr）发现了以他名字命名的Kerr黑洞[1]，这个黑洞度规具有更少的对称性（只有轴对称性），因此可以描述具有自转的黑洞。

R-N黑洞和Kerr黑洞在事件视界内部与史瓦西黑洞具有本质不同。以下主要依据Kerr黑洞，来介绍其具有的一些物理特点。

Kerr黑洞的度规如下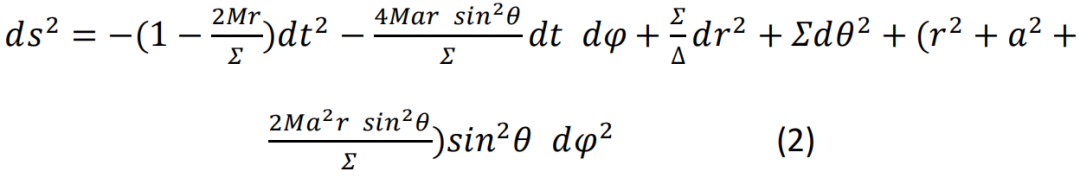：其中Δ=r2-2Mr+a2，∑=r2+a2cos2θ，J=aM，J表示黑洞具有的角动量。只看度规的形式，也可以感觉到Kerr黑洞要比史瓦西黑洞复杂得多，并且在Δ=0的位置，度规会出现发散行为。此外，如果考虑等半径曲面（等r面）的法矢量的方向，我们能发现法矢量nα满足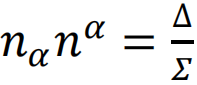，因此Δ=0也是半径r方向从类空方向到类时方向转变的地方。据此可以确定，Δ=0将给出黑洞视界位置。有趣的是，在Kerr黑洞中，Δ=0这一方程有两个根，这表明黑洞存在两个视界：
 

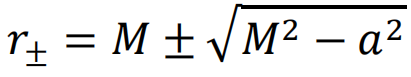
在事件视界之内，还存在一个柯西视界。内视界的存在对于黑洞内部造成了极大的影响。此时事件视界不再是物体有进无出的地方，同时内视界之内的区域时空仍然是静态的、不随时间演化的。

黑洞奇点

我们再来介绍黑洞的另一个特征：奇点。对于史瓦西黑洞，在r=0的位置，度规此时的发散是无法被任何坐标变换消除的。这一点也可以通过计算一些由时空曲率组合成的标量来看，结果发现这些标量在这一点都是发散的。因为标量不依赖于坐标系的选择，因此这个发散是物理上的发散，这一r=0的位置叫作黑洞的奇点。

对于Kerr黑洞，人们进一步发现它的奇点的结构，和史瓦西黑洞具有很大的不同。首先因为内视界的存在，黑洞奇点会从类空奇点转变为类时奇点。同时，奇点的结构也有所不同，这一点从（2）式的球坐标中不容易看出，但是如果我们将之转换为类笛卡尔坐标的话，就会变得很清楚。坐标变换关系如下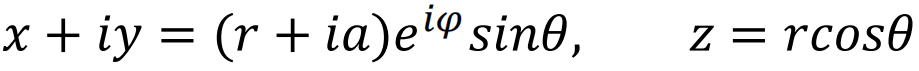：如果a=0，这个坐标关系就和人们颇为熟悉的直角坐标到球坐标系的变换相同，但因为有旋转的存在，结果会发生一点变化。x，y，z具有如下关系：

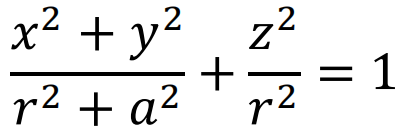
因为旋转的存在，对于等r面，Kerr时空也和球对称时空有些不同。原本的球对称时空中等r面是球面，这里将会变为椭球面。对于r=0的奇点位置，此时满足条件，x2+y2=a2，z=0；当没有旋转的时候，奇点位置对应为x=y=z=0；但是有旋转之后，奇点处x，y可以不为0，x，y平面组成的是一个半径为a的圆。因为这个特点，Kerr黑洞奇异性出现的位置又叫作奇环。

但是，这些解析黑洞解中出现奇点这一理论事实，并不能完全证实奇点的存在。因为在得到这些黑洞的过程中，或多或少都选择了特殊的对称性。一个自然的问题是，奇点是否只是由于对称性所造成的幻觉呢？由于爱因斯坦方程的求解依赖对称性，这个问题实际上并不容易回答。

上世纪六七十年代，苏联物理学家别林斯基（Vladimir Belinski）、哈拉特尼科夫（Isaak Khalatnikov）和栗弗席兹（Evgeny Lifshitz）三人，就试图在不加对称性的情况下讨论这一奇点形成的问题[2]。最终，这个问题随着彭罗斯（Roger Penrose）和霍金（Stephen Hawking）证明奇点定理而结束[3]。奇点定理非常巧妙，彭罗斯和霍金通过测地线汇等整体微分几何的技巧，在不求解爱因斯坦方程的基础上，在相当一般的情况下证实了黑洞一定具有奇异性。值得一提的是，苏联科学家的努力也没有白费，他们发现的BKL拟设（以三人姓氏命名的一类奇点模型）简化了黑洞类空奇点附近的引力动力学行为，使得奇点附近的运动方程能够求解。他们的工作虽然没有排除奇点的存在，但可以帮助人们更直观地认识奇点附近时空度规的变化规律。

奇点不存在？

读者或许会奇怪，根据我们对于奇点的介绍，奇点是各种时空曲率构造的标量发散的位置，既然彭罗斯都没有真正求解爱因斯坦方程，又是如何知道曲率标量发散的呢？事实上，彭罗斯说的奇点和我们介绍的奇点的含义有一些微妙的区别。

关于奇点的定义其实有两种：一是前面提到的通过某些不依赖于坐标选择的标量的发散来定义；另一种则是通过不可延拓时空中的测地线仿射参数的有限性（简称FALLs）来刻画。第二种奇点的定义来自如下的直觉：对于一个正常的时空，一个粒子应该无论何时都处在时空中；如果时空中的一条曲线在某个有限的参数下突然消失于这个时空中 （并且背景时空没有办法进行解析延拓），那么一定是由于时空本身出现了奇异点，使得这条曲线终结在了这个奇异点上。这种奇点定义虽然抽象，但是其定义具有一般性，不依赖于具体的度规解，这一特点使得其在数学证明中非常有用。而第一种定义奇点的方式虽然直观，但是依赖于具体的黑洞解。这两种定义方式差别很大，人们很难直观地建立这两种奇点表述之间的关系。针对这一问题，黑洞研究先驱、马上90周岁的克尔再次发文讨论[4]，并提出黑洞可能不存在奇点。

克尔在文章中指出，对于Kerr黑洞，至少存在一条FALLs并非终结于奇点。他找到了如下一个简单的反例，沿着Kerr黑洞的对称轴运动的光线，其运动轨迹满足如下方程：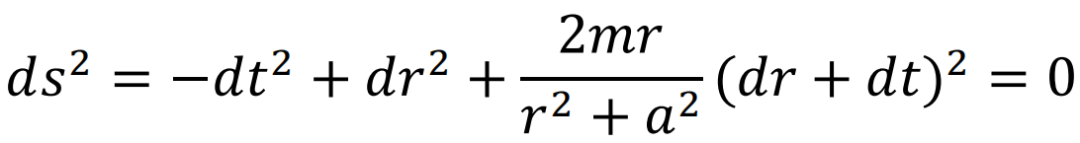
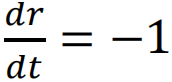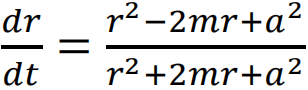由此可以解出两条光线，和。对于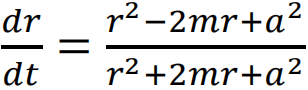这条光线，在内外视界位置因为径向速度dr/dt=0，所以测地线只能处在内外视界之间的区域。此时这条类光测地线具有有限的仿射参数（可以用r坐标作为这条曲线的仿射参数）。因此，克尔在文章中指出，他构造了一个具有有限仿射参数的测地线，但显然它并没有与任何具有曲率奇异性的地方相交。由此克尔指出彭罗斯证明的奇点定理可能是不完整的，虽然彭罗斯的证明指出在很一般的条件下FALLs一定会出现，但是这并不意味着奇点一定会出现。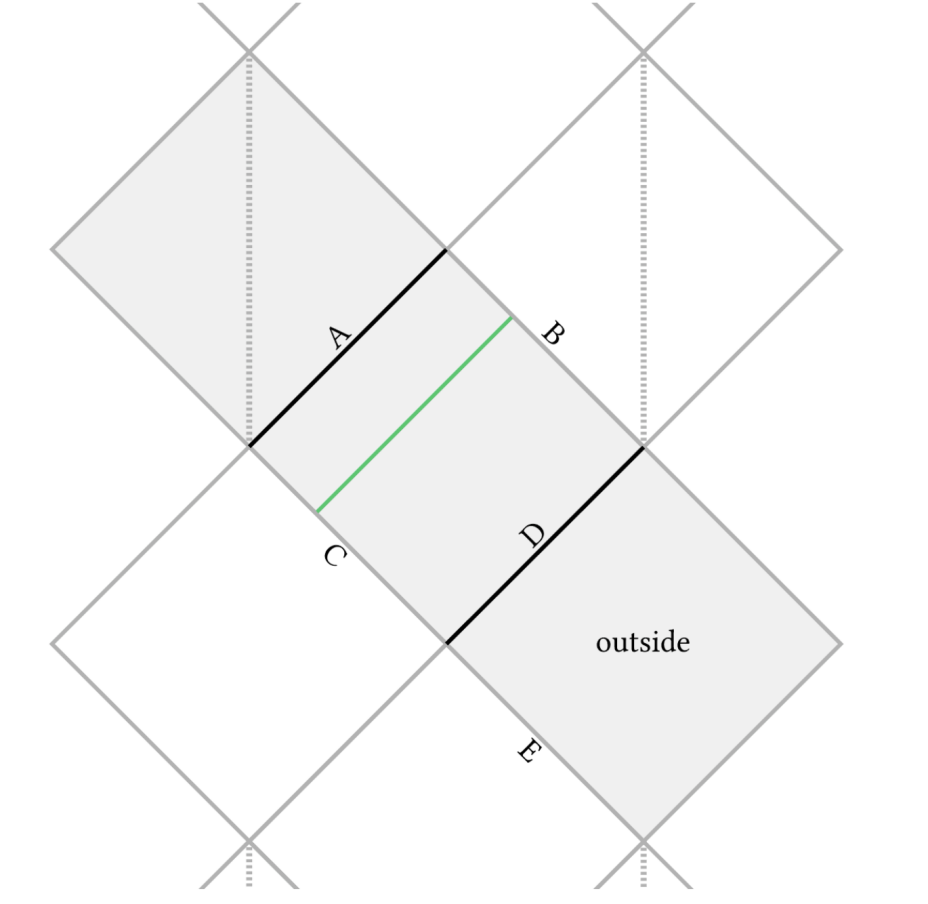

图2 Kerr所提到的反例是绿色的测地线，然而其所用到的坐标系只覆盖了灰色区域，这部分区域并非完整的时空，而是可以被延拓到更大的Kruskal时空（即包含白色部分）。

而针对黑洞内部具体的物理图像，他则提议，由于内视界之内还是静态时空，因此内视界之内可以存在某种星体（如中子星）来代替Kerr黑洞中出现的奇异环。这个星体的度规和外面的Kerr黑洞连接构成真实的物理图像。换句话说，奇异环仅仅只是作为真实的非奇异星体的一个理想近似。

对于克尔的结论，目前仍有一些问题值得探讨。首先在他寻找到的反例之中，所用到的坐标系并没有覆盖整个时空，因此，这一部分坐标系所覆盖的区域并非表示一个不可延拓的时空。此外，克尔寻找到的测地线并非完整的测地线。至少在数学解的意义上研究奇点定理时，探讨奇点是否存在需要保证背景时空是不可延拓的，所以他寻找的反例是否构成一个破坏彭罗斯奇点定理的反例有待讨论。

其次，即便数学解的解析延拓给出的时空结构可能并非物理上真实时空的样子，考虑真实时空的物理图像或许也与克尔提出的想法有一定的偏差。在克尔的提议中，无论是寻找到破坏奇点定理的反例，还是黑洞内部的物理图像，必然依赖于Kerr黑洞的内视界存在。然而众多研究显示[5]，黑洞内视界是不稳定的，这种不稳定性一方面来源于内视界的动力学不稳定性，此时微小的涨落会在内视界附近被放大，使得原本的内视界变为新的曲率奇点所在之处（即质量暴涨效应）。

同时，因为时空中各种物质场的存在，当这些物质场使得黑洞带毛[注1]（如标量毛）之后，也会导致黑洞的内视界消失，因此实际的物理图像也可能并不存在内视界（即内视界和奇点之内的区域），这便会排除内视界以内稳定存在某种星体度规的可能。而且，克尔寻找到的这一类不接触奇点的FALLs也将失效，因为他的例子中的测地线交在内视界，但此时内视界位置将变为新的奇点所在处，因此反例中的测地线实际上将与奇点相交。

黑洞内部：21世纪的黑体辐射？

值得注意的是，克尔的讨论仅仅只是奇点问题的一种解决方式，即使他提议的失效也并不意味着奇点便会存在。彭罗斯和霍金基于经典引力证明的奇点定理更多标志的是经典引力的失效，从这个意义上，可以说黑洞奇点更多承担的是类似黑体辐射紫外发散的历史意义。量子物理作为一个新的范式，任何物理理论都需要在小尺度上被纳入量子物理的范式之中。目前只有以广义相对论为代表的引力理论仍在负隅顽抗。人们认为引力需要量子化，广义相对论与量子力学也一定需要融合。在这一过程中，给各种物理量发散的黑洞奇点一个全新的量子力学版本的理解，从而解决这一发散就是量子引力诞生的必由之路。

经典广义相对论预言的黑洞内部的图像一定是不完整的，在黑洞内部这一宇宙最隐秘的角落，一定隐藏着更多神奇的东西。

注释

[1] 黑洞虽然具有无毛定理，但是这仅仅是在爱因斯坦-麦克斯韦的框架下，在更一般的框架下，有很多构造可以超越这个松散定理的限制。

参考文献

[1] R. P. Kerr, “Gravitational field of a spinning mass as an example of a algebraically special metric”, Phys. Rev. Lett. 11, p. 237 (1963).
 

[2] V.A. Belinskii, I.M. Khalatnikov and E.M. Lifshitz, “Oscillatory approach to a singular point in the relativistic cosmology,” Adv. Phys. 19, 525 (1970).[3] R. Penrose, “Gravitational collapse and space-time singularities”, Phys. Rev. Lett. 14, p. 57 (1965).[4] R.P. Kerr, Do Black Holes have Singularities? arXiv:2312.00841.[5] E.Poisson, W.Israel , “Internal structure of black holes”. Phys.Rev.D 41 (1990) 1796-1809.

本文受科普中国·星空计划项目扶持

出品：中国科协科普部

监制：中国科学技术出版社有限公司、北京中科星河文化传媒有限公司