“他清楚自己拥有那个时代最睿智的头脑,这是他自负的资本,但是他的自卑也是明显的,一旦有很多人站在他的对立面,他就会惴惴不安,反复思考自己是否有这样或那样的错误……”
——爱因斯坦
撰文 | 郑超(中国科学院上海有机化学研究所研究员)
前情提要
我们前不久在《上篇链接》一文中讲述了“物质由不可分割的原子组成”,是起源于古希腊的古老思想。十九世纪初,道尔顿跳出哲学思辨的藩篱,以物质的化学组成问题为依托,提出了近代原子论。一石激起千层浪,以原子为基础理解化学反应的观念助力了十九世纪化学的蓬勃发展。1860年,坎尼扎罗在卡尔斯鲁厄会议上传播阿伏伽德罗的分子学说,进一步推动了原子、分子概念在化学研究中的应用。然而,原子和分子从科学概念最终走向物理实在,还有漫长的道路等待着人们去探索和跋涉。
本文继前文继续讲述……。
唯能论者的阻击
虽然坎尼扎罗在卡尔斯鲁厄会议上澄清了许多关于原子、分子概念的误区,但是远未消除化学家们心中的疑虑。凯库勒在1867年的论述最能体现这种矛盾的心态。他说作为化学家,他“完全认同原子和分子不仅是明智的假设,更是不可或缺的需要”;但是作为哲学观点,他“并不相信原子和分子是构成物质的基本单元”。毕竟当时的化学分析手段非常有限,远不足以论证“道尔顿发明的坚硬小球”的存在。在相当一部分化学家看来,原子和分子不过是表征物质元素组成的一种便利模型罢了。“东方不亮西方亮”。有关分子存在性争论的阵地,在十九世纪下半叶从化学悄然转移到了另一门新兴学科——热力学与经典统计力学。
十八世纪,以蒸汽机为标志的第一次工业革命为人类社会带来了前所未有的巨大变革。热力学几乎就是为了提升蒸汽机——或者更一般地说——热机的工作效率这个现实目标而萌芽并发展起来的。对于资本家而言,一个贪婪却无比美好的愿望是不消耗能量就能源源不断地产生动力。但是以道尔顿的学生焦耳(J. P. Joule)为代表的物理学家通过实验验证了能量守恒,打破了“无中生有”的(第一类)永动机的美梦。那么退而求其次,能否让输入热机的热量全部转化为动力,避免任何浪费呢?法国工程师卡诺(N. Carnot)提出了理想热机的卡诺循环,明确指出无论怎样改变工作介质或者优化机械结构,都不可能使热机的效率达到百分之百。英国物理学家汤姆逊(W. Thomson,后来受封为开尔文勋爵,Lord Kelvin)进一步指出,不可能从单一热源吸收热量,并将其全部用来做功而不造成其他影响,从而宣告了“物尽其用”的(第二类)永动机的破产。德国物理学家克劳修斯(R. Clausius)在卡诺循环的基础上提炼出熵(S)的概念,描述热力学过程中的“能量退化”,同时给出了热力学第二定律的数学表述:任何孤立体系的熵永不减小,并且在平衡态时达到最大值。
ΔS ≥ 0 (4)
简明的(4)式就像一支飞箭,给热力学的世界标注了“方向”。
虽然热力学的诞生有着浓厚的实践背景,但是她很快就发展为一门精巧的“唯象科学(phenomenological science)”。热力学并不关心研究对象的微观结构,而是用诸如内能、熵和温度之类的状态函数刻画体系在接近平衡态时的宏观性质。热力学是如此的难以捉摸,她既能斩钉截铁地告诉你“努力做功”的极限,又会在不经意间将你诱入“热寂说”的哲学陷阱。于是,原子、分子学说的信奉者们非常自然地希望从物质的微观结构出发,构建热力学的理论基础(mechanical theory)。他们必须解决的难题是,如何用统计的手段将大量分子的运动行为与体系的宏观热力学性质联系起来,而这项努力的最终成果正是经典统计力学。


左边:L. E. Boltzmann(1844~1906);右边:F. W. Ostwald(1853~1932)1909年诺贝尔化学奖获得者
在经典统计力学的发展道路上,克劳修斯最早认识到,理想气体的内能可表达为所有气体分子随机运动的动能之和。英国物理学家麦克斯韦(J. C. Maxwell)则推导出了在一定温度的平衡态下,理想气体分子的速度分布公式,可据此计算出平衡态下处于给定速度区间的气体分子数。一切准备工作就绪,历史的接力棒在十九世纪七十年代交给了奥地利物理学家玻尔兹曼(L. E. Boltzmann)。经典统计力学的理论框架将在他的手中完成奠基,而这位相信并且捍卫分子理论的独行者也将因此饱受折磨。
玻尔兹曼对于经典统计力学最重要的贡献包括熵的统计定义,和描述理想气体分子速度分布随时间演化的H定理。早先,克劳修斯从热机的工作场景出发,通过可逆过程中体系得失的热量与温度之比来定义熵:dS = δQrev/T,它体现了处于确定宏观状态时体系的某种“混乱程度”。而玻尔兹曼认为由于构成体系的大量分子的随机运动,体系每一种确定的宏观状态一定对应着为数甚巨的不同微观状态。体系的宏观混乱程度正是其微观状态多样性的表现。因此体系某一宏观状态的熵S必然与对应的微观状态的数量W相关联,熵值最大的平衡态所对应的微观状态数也必然为最大值。如果假定每种微观状态出现的概率相等,那么平衡态就是体系所有可能的宏观状态中出现概率最大的那种。为了满足熵作为广延量的要求(整体等于部分之和),玻尔兹曼认为体系的熵应当与其微观状态数的自然对数成正比。这一比例关系后来被德国物理学家普朗克(M. Planck)写作如(5)式所示的等式(玻尔兹曼公式):
S = kB log W (5)
其中的比例系数kB称作玻尔兹曼常数,其值约为1.38 × 10–23 J⋅K–1。熵这个概念让所有热力学初学者都颇感费解,而玻尔兹曼公式为其提供了一个清晰的定义。
平衡态是热力学最为关注的状态。麦克斯韦的公式虽然给出了体系处于平衡态时分子运动速度的分布规律,却无法告诉我们体系是怎样演化到,以及为什么一定能够演化到平衡态。玻尔兹曼用经典力学描述理想气体分子的运动和碰撞,在假设相互碰撞的分子独立无关(分子混沌)的条件下,得出了分子运动速度分布f随时间演化的方程(一般称为玻尔兹曼方程),其平衡态的解(满足条件∂f/∂t = 0)正是麦克斯韦分布。玻尔兹曼进一步定义了一个关于f的泛函H(如(6)式,其中dΓ为相空间体积微元),
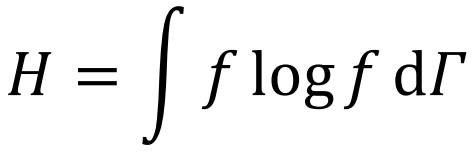 (6)
(6)
并证明了热力学体系向平衡态演化的过程中H函数只减不增,且在平衡态时达到最小值(dH/dt ≤ 0),这就是著名的H定理。更为重要的是,H函数与熵呈线性负相关。H定理因此等价于断言热力学体系的演化过程中熵只增不减,平衡态是熵最大的状态(dS/dt ≥ 0)。换句话说,波尔兹曼从满足经典力学的大量分子的运动行为出发,导出了热力学第二定律!

图5. 位于维也纳中央公墓的玻尔兹曼的墓碑,上方是熵的统计定义公式
玻尔兹曼的结论有多么令人震撼,他本人就遭受了多少非议和诘难。H定理最显著的逻辑“漏洞”是所谓的“逆转问题”。我们知道经典力学规律具备时间反演对称性。如果每个分子的运动都遵循经典力学,那么由这些分子组成的集合体为什么会有确定的演化方向?如果体系从A状态向B状态的演化是熵增过程,那么在B状态时令所有分子的运动速度取负值,根据时间反演对称性,体系将反向演化到A状态,而这个逆过程必将是熵减小的!玻尔兹曼对这一“悖论”的解释是H定理并非力学规律,而是统计规律。宏观体系向熵增方向的演化是大量分子运动行为的统计平均结果。虽然直到今天对H定理的内涵还没有一个令所有人满意的解读,但在十九世纪末,这并不是玻尔兹曼所面临的最致命的挑战。相较于对数学公式理解的差异,与同时代的学者们在哲学观点和世界观上的争论更给玻尔兹曼带来了不可承受之重。
1893年起,玻尔兹曼分别在奥地利维也纳大学和德国莱比锡大学任教。正是在这两所学校,他遇到了分子理论和统计力学最强有力的反对者:莱比锡大学的奥斯特瓦尔德(F. W. Ostwald)和维也纳大学的马赫(E. Mach)。奥斯特瓦尔德虽然是一名化学家,但是他的研究与当时德国化学界的“显学”——有机化学——颇为疏离。他从未在实验室中发现或者合成任何一种新物质,而是特别注重运用物理学的方法,解决化学研究中的“宏大”问题。奥斯特瓦尔德被公认为“物理化学”学科的创立者,他由于在化学平衡和反应速率方面的基础理论,以及催化领域的杰出贡献,被授予1909年诺贝尔化学奖。奥斯特瓦尔德于1887年到莱比锡大学任教时,发表了题为“能量及其转化”的演说,并从此致力于“能量学”的研究。热力学在物理化学研究中所展现的巨大威力给奥斯特瓦尔德留下了深刻的印象。这使他相信,只用能量的概念就可以解释自然界的一切现象。宇宙的根本构成要素是以各种形式存在的能量,自然规律就是支配能量流通和转化的规律;原子、分子只是数学的虚构,物质不是能量的负荷者,而是能量的表现形式;能量学原理比分子理论更能为化学和其他科学提供坚实、明确的基础。奥斯特瓦尔德进一步将能量学的思想上升到哲学高度,逐渐形成了“唯能论”或者“能量一元论”的世界观。尽管奥斯特瓦尔德与玻尔兹曼保持了不错的私交,甚至在玻尔兹曼身处困境时帮助他在莱比锡大学谋得教职。但是,1895年在德国北部港市吕贝克举行的自然哲学家会议上,奥斯特瓦尔德公开反对分子论,和玻尔兹曼展开了激烈的辩论。分别以玻尔兹曼和奥斯特瓦尔德为首的分子论者和唯能论者互不相让,他们的论战贯穿了十九世纪的最后十年。
马赫是十九世纪末极具影响力的实验物理学家和哲学家。他在光学和流体力学的研究中取得了一系列重要的成果,如今在航空领域人们耳熟能详的名词“马赫数”(表示流体速度与局部音速之比的无量纲数)就是以他的名字命名。马赫从经验主义的哲学观点出发,对分子论进行了严厉的批判。他认为如果分子是无法被直接感知或者观测的微小实体,那么假设它们的运动服从描述宏观物体的经典力学规律就毫无根据。因此马赫认为,玻尔兹曼以“分子的运动和碰撞可以用经典力学描述”为基础得出的结论,最多不过是一种有用的数学模型,远远谈不上分子存在的证据。面对分子论者的辩解,马赫经常抛出的“杀手锏”就是:Have you seen one molecule(你见过分子吗)?这时,分子论者只能悻悻而退,承认他们(暂时)还做不到这一点。毕竟从实证角度出发,反对分子论在十九世纪末与人们的经验和逻辑并不矛盾。
玻尔兹曼的性格好强而敏感,与分子论反对者的持续争论对他的精神状态造成了严重的伤害。除了长期的抑郁情绪,晚年的玻尔兹曼还要忍受失眠、心绞痛和哮喘的折磨。1901年,玻尔兹曼离开莱比锡,回到母校维也纳大学接任马赫退休后空出的教职。虽然逃离了唯能论的大本营,但是音乐之都也没能给擅长钢琴的玻尔兹曼带来足够的抚慰。1906年9月,玻尔兹曼和家人到意大利东北部海滨城市特里雅斯特度假。在假期的最后一天,情绪失控的玻尔兹曼趁妻子和女儿去海边游泳的空档,在旅馆的房间里上吊自杀。玻尔兹曼被安葬在维也纳中央公墓,墓碑上镌刻着以他的名字命名的熵的统计定义公式。
历史是如此令人唏嘘。假如玻尔兹曼能多活两年,那么他将看到证实分子客观存在的决定性实验证据。这能否医治好玻尔兹曼的精神创伤,我们永远无从得知,但是奥斯特瓦尔德的确因此转变了观念。1909年,奥斯特瓦尔德在他撰写的著名教科书《普通化学概论》(第三版)的序言中承认:“我们最近已经掌握了证明物质不连续本质的实验证据”。已是风烛残年的马赫则仍然坚守自己的哲学观点。1913年他出版了《物理光学原理》一书,在序言中马赫清晰地表明:“我拒绝今天的原子论信仰。”

图6.(左)奥斯特瓦尔德著《普通化学概论》(第三版,英译本)序言页面;(右)马赫著《物理光学原理》(英译本)序言页面。图中用蓝线标记的是正文引用文字的出处
载入史册的数字
十九世纪关于分子存在性的争论从化学转战至热力学与统计力学,迁延数十年而无定论,一个重要的原因是缺乏直接观测分子的有效方法。如果能测量出某种分子的大小和质量,抑或计算出一定量的宏观物质所包含的分子数目,局面必然为之一变。到哪里去寻找这样的方法呢?读者朋友们也许还记得,高中化学课在引入分子概念时,会介绍一个“用油膜法估测油酸分子大小”的实验。油酸(C18H34O2)是一种两亲性分子,把一滴油酸的酒精溶液滴在水面上,随着酒精溶解于水中,油酸会在水面散开。油酸分子中亲水的羧基(–CO2H)在水面下,疏水的长链烃基(C17H33–)在水面上,大量油酸分子便整齐地“站立”在水面,形成一层薄薄的单分子油膜。如果测出所使用的油酸体积V(如4 × 10–5 cm3)和形成的油膜面积A(如1.65 × 102 cm2),就可以估测出油酸分子的线度d = V/A(约为4 × 10–5 cm3 / 1.65 × 102 cm2 = 2.42 × 10–7 cm)。
油脂在水面铺展成膜是十分常见的现象。1773年,美国开国元勋之一富兰克林(B. Franklin)在给友人的信中,详细描述了他16年前的一次见闻:在海上航行的船队中,有一两艘船的尾部没有明显的航迹,船体仿佛在海面滑翔。有经验的船长告诉富兰克林,这一定是船上的厨师在倾倒泔水,油脂润滑了船底的缘故。富兰克林在伦敦南部的克拉珀姆进行了实验。在一处被风吹皱的湖面,富兰克林将油倒入水中,虽然油量不过一小勺,但迅速铺展的油膜立刻让几平方码的水面平静下来。此后,他经常在竹制手杖中藏一小壶油,一有机会就向朋友们表演“平静水面”的把戏。虽然魔术师富兰克林时常赢得喝彩,但是考虑到他的生平年代(富兰克林卒于1790年)和分子论发展的时间线,富兰克林绝无可能利用油膜法估测分子的数量或者大小。
历史上第一个估算出空气分子大小和标准状况(0 °C,1大气压)下1 cm3空气中所含分子数量的人是奥地利物理学家洛施密特(J. J. Loschmidt)。他也是玻尔兹曼在维也纳大学求学时的老师。洛施密特计算的依据是阿伏伽德罗定律和理想气体的分子运动论。他从克劳修斯的气体分子平均自由程(分子在相邻两次碰撞之间运动的平均距离)公式出发,假定空气分子为球体,导出其直径s和平均自由程l满足以下简单关系:
s = 8εl (7)
(7)式中ε = Nπs3/6,称为物质的压缩系数,它代表单位体积气体所包含的N个球体分子自身实际占据的体积,在宏观上近似等于物质的液态密度和标准状况下气态密度之比(假设液态分子小球紧密相连)。关于空气分子的平均自由程,当时已有较多研究,洛施密特采用的数值为1.40 × 10–7 m。若要求得空气分子的直径,则必须知道空气的压缩系数ε。遗憾的是十九世纪六十年代人们尚未实现对空气的液化,无法通过实验测定液态空气的密度。洛施密特将空气看作由77%的氮元素和23%的氧元素组成的“化合物”,根据科柏(H. Kopp)测定的原子定容,巧妙地估计了液态空气的密度,进而求得空气的压缩系数为8.66 × 10–4。于是可计算出空气分子的直径为8 × 8.66 × 10–4 × 1.40 × 10–7 m = 9.69 × 10–10 m(约为前文估算的油酸分子线度的三分之一,对于真实的氮气和氧气分子而言,该值偏大了不少)。根据这一数值,可知标准状况下1 cm3空气中所含分子数量为1.83 × 1018,这一数值有时被称作洛施密特常数(洛施密特认为他的计算结果可能有一个数量级的误差,该常数的现代值约为2.7 × 1019)。洛施密特的结果在当时并没有可靠的实验验证,所以影响力相对有限。想要准确计算出分子的数量,比如每“克分子”物质中所含的分子数(克分子是以克为单位、数值等于其分子量的物质质量,如氢气的分子量为2,1克分子氢气即2克氢气),还需把目光聚焦于显微镜下,是水面上花粉微粒的无规运动,最终带来了一枚沉甸甸的诺贝尔奖和一串载入史册的数字。
1827年,英国植物学家布朗(R. Brown)用显微镜观察悬浮在水中的花粉微粒。他发现这些微粒在不停地运动,而且轨迹杂乱无章。起初布朗认为这可能是花粉作为生命体活力的表现。但是,当他换用已经死亡的花粉微粒,或者无生命物质(如煤、岩石以及金属)的粉末时,也能看到同样的现象;并且运动的剧烈程度随着微粒尺寸、液体黏度的减小,或者温度的升高而增加。这种永不停歇的运动被命名为布朗运动。十九世纪下半叶,分子论者逐渐相信,布朗运动是由于微粒受到周围液体分子持续不平衡的碰撞所致。正如阴极射线是汤姆逊(J. J. Thomson)发现电子的线索,布朗运动很可能成为表征分子存在的证据。只不过这项证据距离被普遍接受,还缺少一套定量理论和一组受控实验的检验。


左边:A. Einstein(1879~1955)1921年诺贝尔物理学奖获得者;右边:J. B. Perrin(1870~1942)1926年诺贝尔物理学奖获得者
1905年,刚刚在苏黎世大学获得物理学博士学位的爱因斯坦(A. Einstein)迎来了他的“奇迹年”。他在德国《物理年鉴》期刊发表了四篇论文,极大地推进了二十世纪物理学基础的构建。其中《热的分子运动论所要求的静止液体中悬浮粒子的运动》一文首次为布朗运动提供了完善的解释。爱因斯坦认为,由于布朗粒子十分微小(线度约为10–4 cm),它受到来自不同方向的液体分子的撞击不能完全抵消。在显微镜下观察到的是宏观可分辨时间内,布朗粒子受到分子频繁撞击所展现的平均位移,是统计规律下的涨落现象。爱因斯坦推导出了关于布朗粒子扩散的微分方程,以及粒子在给定时间内朝某一方向位移的分布公式,由此可知布朗粒子的平均位移λ与时间t的平方根成正比
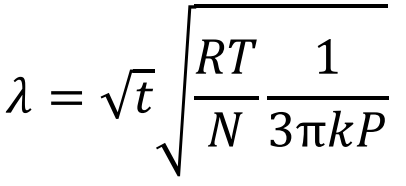 (8)
(8)
在(8)式λ和t1/2的比例系数表达式中,除了普适气体常数R,以及绝对温度T、液体内摩擦系数k、布朗粒子的有效半径P等可观测量之外,就只剩下未知的每克分子物质所含的分子数N了!爱因斯坦的公式指出了一条从布朗运动的可观测量出发,计算分子数量和大小的道路。
三年后,法国物理学家佩兰(J. B. Perrin)走完了证实分子客观存在的最后一步。佩兰早年就读于巴黎高等师范学校,后来长期在巴黎索邦大学任教。1895年佩兰证明阴极射线中存在带负电荷的粒子,为汤姆逊发现电子奠定了基础。1908年,他在爱因斯坦关于布朗运动的理论启发下,通过实验测定了每克分子物质所含的分子数(即(8)式中的N)。为了纪念分子学说的创始人阿伏伽德罗,佩兰建议将此数值命名为阿伏伽德罗数,记为NA。佩兰实验设计的关键在于,将检验布朗运动效应的方向从水平变为竖直;摒弃诸如花粉微粒之类的天然(不可控)布朗粒子体系,改用特殊制备的单分散(标准化)乳浊液作为研究对象。佩兰认为乳浊液中的粒子由于受到重力(沉降)和布朗运动(扩散)的共同影响,在竖直方向存在数密度分布的差异(平衡态下高处的粒子数比低处少),如同大气密度随海拔提升而逐渐稀薄一样。他进一步推导出了乳浊液粒子竖直方向数密度分布的公式:
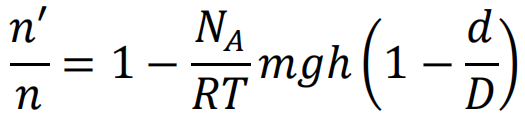 (9)
(9)
式中R和g为普适气体常数和重力加速度。假设已知乳浊液中粒子的质量m和密度D、液体密度d以及环境温度T,并通过实验测定乳浊液中高度差为h的两个水平面上的粒子数n′和n,就能计算出阿伏伽德罗数NA。
知易行难。虽然实验原理并不复杂,但要想得到一锤定音的结果,非下一番苦功夫不可。佩兰利用离心的方法,花费数月时间分选出几十克粒径高度均一的藤黄(一种绘画颜料)和乳香(一种天然树脂)微粒(粒径小于0.5 μm),并准确测量了其质量和密度。他巧妙地在显微镜的载玻片上构建出0.1 mm高的乳浊液样品,利用景深极浅的高倍镜头实现对乳浊液中单层粒子的观测。为了克服粒子布朗运动本身对观测的干扰,佩兰设法将显微镜视场限制在针尖大小的区域,用肉眼经显微镜观察某一瞬间出现在此区域中的粒子数量,经过几千次的计数,即可求出乳浊液某一高度处的粒子数n。大道至简,重剑无锋。佩兰就是利用这样精巧又质朴的方法,对不同种类、粒径和黏度的乳浊液在不同温度下进行了大量重复观测,根据(9)式计算出NA的数值为6.5~7.2 × 1023。佩兰和他的学生肖赛格(M. Chaudesaigues)还用显微镜直接观测了乳浊液粒子布朗运动的平均位移λ,根据(8)式计算出NA的数值处于5.5~8.0 × 1023这样一个狭小的区间。如果扣除实验误差,可以认为NA对于不同物质是一个定值,阿伏伽德罗数因此可以升格为阿伏伽德罗常数。

图7. 佩兰在显微镜下拍摄的藤黄乳浊液微粒处于沉降–扩散平衡状态时的照片。图片来源:Advances in Colloid Science(左);Stud. Hist. Phil. Sci. 2008, 39, 312–322(右)
佩兰对于藤黄和乳香乳浊液的观测过程本身并不要求预先假设分子的存在,但是其观测结果,特别是使用不同方法对NA的计算给出了高度一致的数值,就证明了爱因斯坦关于布朗运动理论的正确性,从而论证了分子的客观存在。与唯象理论者只接受可直接感知和观测的实验现象不同,佩兰指出,他的工作在肉眼可见的复杂现象与无法直接触及的简明原理之间建立了因果联系(… to explain the complications of the visible in terms of invisible simplicity)。唯能论的首领奥斯特瓦尔德在佩兰的实验之后接受了分子的存在。法国大科学家庞加莱(H. Poincaré)——此前他和马赫一样认为分子只是一种无关紧要的、随时可以放弃的数学假设——高度评价佩兰的工作,他说:“佩兰测定了(一定量物质所包含的)分子的数目,这一杰出的工作宣告了分子理论的胜利。”1926年,佩兰由于对“物质不连续结构”和“发现沉降平衡”的贡献,被授予诺贝尔物理学奖。这时距离道尔顿写出第一张原子量表过去了123年,距离坎尼扎罗在卡尔斯鲁厄会议上传播阿伏伽德罗的分子学说过去了66年,距离玻尔兹曼自杀过去了20年。
二十世纪初,更多关于微观世界的实验证据和表征手段的出现,以及量子力学带来的伟大变革,使得原子和分子的客观存在性不再是一个争议问题,而逐渐成为普罗大众都有所认知的常识。1971年,第14届国际计量大会废止了“克分子”,重新定义“摩尔”(mole,简写为mol)作为物质的量的单位(摩尔也由此成为国际单位制中7个基本单位之一):规定与12克12C所含碳原子数量相同的基本实体系统为1 mol,阿伏伽德罗常数因此获得了单位mol–1。随着测定阿伏伽德罗常数的新方法不断涌现,数值精度也显著提高。目前最精密的方法是用X射线干涉仪测量硅晶体的晶格密度,通过对晶体中的硅原子直接计数实现的,其不确定度可以减小到10–8量级。2019年,摩尔等国际单位制基本单位改由物理常数定义,阿伏伽德罗常数的数值被固定为:
NA = 6.022 140 76 × 1023 mol−1 (10)
原子、分子从思辨走向科学,经历了跨越百年的追索。随着时间的流逝,今天的人们似乎越来越把原子、分子当作理所当然的存在,而不再关心它们的历史沿革。笔者在翻阅有关道尔顿、阿伏伽德罗、盖–吕萨克和贝采利乌斯等人的资料时,一度对他们所关心的问题、使用的方法、发明的术语都深感隔膜、难以理解,这大概是笔者接受了20年当代化学科班训练的结果!但是无论如何,前辈科学家们那些真正“从零到一”的探索,哪怕是他们犯的错误、起的争执,都无一不值得我们细细品味。那些在黑暗中历尽艰辛才偶有所得的、痛并快乐的历程,可能用英国数学家怀尔斯(A. Wiles)的一段话来描述最为恰当:
“当你初入一间完全黑暗的房间,你会到处跌跌撞撞。在这个过程中,你逐渐熟悉了每一件家具的位置。终于,也许经历了六个月的摸索,你找到了吊灯的开关。当你打开吊灯,霎时间屋里的一切被照亮,所有的陈设无不印证了你的猜想。欣喜之余,你义无反顾地打开了通往下一个黑暗房间的大门……”
参考文献
[1] J. R. Partington, Ann. Sci. 1939, 4, 2435.
[2] A. J. Ihde, J. Chem. Educ. 1961, 38, 83.
[3] S. G. Brush, Synthese 1968, 18, 192.
[4] A. J. Rocke, Hist. Stud. Phys. Sci. 1978, 9, 225.
[5] W. W. Porterfield, J. Chem. Educ. 1995, 72, 871.
[6] M. C. Usselman, D. G. Leaist, K. D. Watson, ChemPhysChem 2008, 9, 106.
[7] M. C. Usselman, T. A. Brown, Ann. Sci. 2015, 72, 153.
[8] M. I. Grossman, Brit. J. Hist. Sci. 2017, 50, 657.
[9] Y. Xu, Y. Tong, J. Yuan, Found. Chem. 2023, 25, 439.
[10] D. S. L. Cardwell, Ed. John Dalton & The Progress of Science. Manchester University Press, 1966.
[11] A. J. Rocke, Chemical Atomism in the Nineteen Century – From Dalton to Cannizzaro. Ohio State University Press, 1984.
[12] C. Cercignani, Ludwig Boltztnann The Man Who Trusted Atoms. Oxford University Press, 1998.
[13] P. Achinstein, Book of Evidence. Oxford University Press, 2001.
[14] P. Grapí, Inspiring Air: A History of Air-related Science. Vernon Press, 2019.
[15] R. Seth, G. E. Smith, Brownian Motion and Molecular Reality. Oxford University Press, 2020.
[16] 李醒民,《自然辩证法通讯》,1988年,第10卷,57页。
[17] 刘立,《大学化学》,1989年,第4卷,61页。
[18] 沈乃澂,《物理》,2018年,第47卷,648页。
[19] 王竹溪著,《热力学》,高等教育出版社,1955年。
[20] 道尔顿著,李家玉、盛根玉译,《化学哲学新体系》,北京大学出版社,2006年。
[21] 牛顿著,周岳明、舒幼生、邢峰、熊汉富译,徐克明校,《牛顿光学》(第二版),北京大学出版社,2011年。
[22] 贺拉斯著,李永毅译注,《贺拉斯诗全集——拉中对照详注本》,中国青年出版社,2017年。
致谢
作者感谢中国科学院上海有机化学研究所游书力院士、中国科学院物理研究所曹则贤研究员、上海交通大学张绍东教授和中国科学院自然科学史研究所刘金岩研究员对本文的宝贵意见。
作者简介
郑超博士,中国科学院上海有机化学研究所研究员,国家自然科学基金委员会优秀青年科学基金项目获得者。研究方向为物理有机化学与手性合成。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 