
我们到底还是无法理解数学真正的基础、真正的含义是什么,数学与音乐一样,都属于人类创造性活动的产物,其成果受到历史发展的影响,因此我们很难客观对其进行合理化。
——赫尔曼·外尔
撰文 | 小平邦彦
译者 | 尤斌斌
1949 年 9 月,我接受了赫尔曼·外尔的邀请去了普林斯顿的高等研究院。邀请信上外尔老师的签名给我留下了深刻的印象。第一次在研究院见到外尔老师时感到有些意外,他身材高大,长着一张圆脸,是一位体态文雅的绅士,给人的感觉像是一个性格和善的大叔。
我在去普林斯顿的路上顺便拐到芝加哥大学拜访了韦伊老师。韦伊老师从三楼窗户探出头来招呼我,他戴着魔鬼面具,吓了我一跳。即便如此,我并未对他感到些许意外。我对外尔老师的长相虽然有些意外,但并非那种因为与预想形象不同而感到的意外,而是一种莫名的意外感觉,说不太清楚。
对外尔老师而言,他们看到眼前这个身材瘦小、英语不流利的亚洲人时,也许也感到一丝意外。所以他才盯着我的脸打量一番,然后建议我“等下学期英语好点的时候再开专题研讨课”。
外尔老师几乎每天中午都跟我们这些年轻研究员一起在研究院四楼的食堂就餐,同时愉快地谈论各种话题。他会把洒在托盘上的咖啡重新倒入碗中喝掉。回想起来,这些事情仿佛是昨天刚刚发生的一样。
外尔老师生性率直,他不会将自己的想法藏在心里,有时候会说出一些辛辣的话语。有一天中午,我们在食堂吃午饭时,坐在我身边的一位年轻的美国数学家提到说:“今天是小平 40 岁生日。”于是,外尔老师突然转向我,并对我说:“据我所知,数学家想要做出一番成就一般要在 35 岁以前,你最好抓紧时间(you'd better hurry)。”不管如何抓紧时间,我都无法再回到 35 岁,这对我来说太困难了。老师貌似也意识到自己说得有些过分了,就继续补充说:“不过也有例外,也许你就是例外。”这还算是比较收敛了,我还听说外尔老师曾经微笑着对一个意气风发的新人数学家说:“我不太看好你的数学研究。”这简直太吓人了。
外尔大概是 20 世纪最后一位重量级的大数学家了,他的研究领域不仅限于数学,还涉及物理学和哲学。在爱因斯坦发表广义相对论后,外尔随即编著了《空间、时间与物质》,尝试研究统一场论。量子力学出现后,他又撰写了《群论与量子力学》。他发表论文共167 篇,合计约 2800 页,出版著作多达 16 册,为后人留下了丰厚的硕果。
20 世纪 40 年代盛行研究巴拿赫空间、希尔伯特空间等函数解析,普林斯顿高等研究院的许多年轻研究员都以此作为自己的研究领域,外尔和西格尔仿佛在数学研究上完全与其他人独立。我曾经在研究院正面的院子里遇到日本数学家,至今还清楚地记得他说过:“外尔和西格尔两个人乐此不疲地在挑战古老复杂的数学,那是种反动行为。”进入 20 世纪 50 年代后,代数几何、流形论、微分拓扑等迅速发展,数学出现了天翻地覆的变化。
在我赴美前,外尔老师就一直很照顾我。斯通在其关于希尔伯特空间的著作的最后一章中提到雅可比矩阵(Jacobi matrices)理论,即二阶差分方程理论。将其改成二阶常微分方程,同时结合外尔在年轻时撰写的有关二阶常微分方程固有值问题的论文发现,可以得到具体公式给出固有值分布与固有函数的展开,于是我写成一篇论文发给了外尔老师。之后外尔老师回信告诉我蒂奇马什(Titchmarsh)使用其他方法得出了相同的公式,并且给我寄来了蒂奇马什的著作。后来我又收到外尔老师来信,大致的内容是:“我想在这次数学年会上演讲时引用你前几天的论文,我可以引用你未发表的论文吗?”即便是我这样的亚洲无名数学家,外尔老师也考虑得非常周到。在 1948 年 12 月美国数学学会的年会上,外尔老师发表了该演讲 。
到了下学期,按计划我在外尔和西格尔的指导下开始上有关调和微分形式的专题研讨课。刚开始几次课由外尔老师讲授历史沿革,因为当时我的英语还很糟糕,所以很遗憾,我不太记得上课的具体内容。外尔的部分结束后,由德拉姆(de Rham)讲授了七八节课基于当时现有方法的黎曼流形上调和微分形式理论,最后由我讲授调和微分形式在复流形中的应用。整个课程结束后,外尔老师对我说:“之前的调和微分形式专题研讨课上到一半就乱套了,幸亏这次专家阵容齐全,最终圆满完成任务。”
之前的专题研讨课指的是 1942 年左右开设的有关霍奇(Hodge)调和积分论的专题研讨,刚开始主要研读霍奇的著作,后来发现调和微分形式的存在证明存在一定的缺陷(gap),于是专题研讨课就因此暂停了。外尔老师还专门写了一篇论文去填补该缺陷。
外尔老师用了几周时间在研究院讲授数学的 50 年历史,即1900 年至 1950 年间数学的历史。我记得这部分课程大概是在1952 年的上半学期,当时希策布鲁赫也来旁听。后来我因为当时没记笔记而感到遗憾,不过印象比较深刻的内容包括关于整数论的详细分析、对奈望林纳(R.Nevanlinna)理论的高度评价、抽象的普遍化理论很无聊,等等。不过我也不记得在讲什么内容时提到抽象的普遍化理论很无聊,他曾提到:“你们肯定会想问,那你为什么要写《黎曼曲面的概念》这样的普遍化理论呢?当时在讲黎曼曲面时,我就想‘思考普遍化的黎曼曲面’,于是就做了这件事(双手侧平举后上下摆动)。尽管如此还是觉得很麻烦,因此就写了《黎曼曲面的概念》。”这样听来,感觉外尔老师将《黎曼曲面的概念》归类于无聊的抽象论,这令我感到十分震惊。众所周知,《黎曼曲面的概念》是现代复流形理论的原型,书中几乎完美地展现了一维复流形理论。
另外对于自己的定理“假设θ 是无理数,点列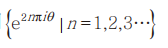 在单位圆周上平均分布”,外尔谈道:“在以前,类似这样的简单定理就是一个大发现,而现在的你们必须从事复杂的研究工作,太不容易了。”在这个课上我还听到了类似这样的故事:“阿廷说在巴赫之后就没有出现新的音乐了,于是我就问他数学是什么情况,结果他摆出了一副嫌弃的表情。”数学家阿廷(Emil Artin)精通音乐,会弹奏拨弦古钢琴,他的兴趣是研磨天体望远镜的镜片。
在单位圆周上平均分布”,外尔谈道:“在以前,类似这样的简单定理就是一个大发现,而现在的你们必须从事复杂的研究工作,太不容易了。”在这个课上我还听到了类似这样的故事:“阿廷说在巴赫之后就没有出现新的音乐了,于是我就问他数学是什么情况,结果他摆出了一副嫌弃的表情。”数学家阿廷(Emil Artin)精通音乐,会弹奏拨弦古钢琴,他的兴趣是研磨天体望远镜的镜片。
到了普林斯顿后,我又重新将调和微分形式的论文印成小册,并带着它去拜访了外尔老师。老师手拿着小册,笑眯眯地夸我说:“从运用正交射影的方法来看,确实做得不错。”又说:“也许我是一个守旧派,不过我觉得正交射影的方法不太好,我建议你重新修改论文,最好也不要采用正交射影的方法。”这番话使我备受打击。外尔老师在 1955 年出版的《黎曼曲面的概念》修改版的序中曾经写道:“我也曾考虑过从本质上将狄利克雷原理改成正交射影的方法,不过最终还是放弃了。我不打算解释个中缘由。”
正交射影是外尔发现的方法,对证明调和微分形式的存在极其有用。外尔老师说这个方法不太好,其原因在于他自身的数学哲学。对于数学基础研究,外尔老师支持直觉主义,虽说我也是支持直觉主义,不过这也只是针对数学基础研究,平时在做数学研究时,跟一般的数学家并无任何区别,而外尔的直觉主义可不是如此肤浅。康斯坦·里德在库朗传记中写道:“外尔站在直觉主义的立场上为新生讲授解析入门。”
正交射影的方法到底所指何物?对此进行说明前,首先需要证明紧黎曼空间R 上存在具有给定周期的第一种调和微分形式。假设将R 上勒贝格可测由整个具有有限范数的 r 次微分形式ϕ 构成的希尔伯特空间记作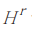 ,将由二次连续可微的微分形式构成的
,将由二次连续可微的微分形式构成的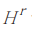 的部分空间记作
的部分空间记作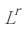 ,那么
,那么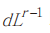 以及
以及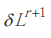 是
是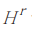 互相正交的部分空间。假设将同时与
互相正交的部分空间。假设将同时与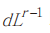 和
和 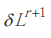 正交的
正交的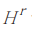 的部分空间记作
的部分空间记作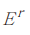 ,那么
,那么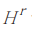 是同时正交的三个部分空间的直和,即
是同时正交的三个部分空间的直和,即
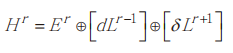
上述公式中的 [] 代表闭包。ϕ ∈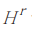 对
对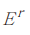 的正交射影记作 Pϕ 。德拉姆定理表明,存在具有给定周期的连续可微的 r 次微分形式ψ ,dψ = 0 。如果取正交射影
的正交射影记作 Pϕ 。德拉姆定理表明,存在具有给定周期的连续可微的 r 次微分形式ψ ,dψ = 0 。如果取正交射影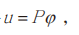 u 所求的给定第一种调和微分形式就是正交射影的方法。
u 所求的给定第一种调和微分形式就是正交射影的方法。
外尔老师深受哥德尔的不完全性定理“任何一个包含自然数论的形式系统,当该形式系统无矛盾时,它的无矛盾性不可能在该形式系统内证明”影响,他在其著作《数学与自然科学的哲学》英文版中提到:“我们到底还是无法理解数学真正的基础、真正的含义是什么,数学与音乐一样,都属于人类创造性活动的产物,其成果受到历史发展的影响,因此我们很难客观对其进行合理化。”此外,在有关数学与逻辑概述的论文的结语中,外尔写道:“(源于集合论悖论)的数学危机给我的数学研究带来了相当大的实际性影响,因此我将自己的兴趣转向了相对“安全”的研究领域。
从直觉主义来看,“存在”实数或函数意味着“能构成”该实数或函数。因此不存在任意不特定的勒贝格可测微分形式,构成其整体的希尔伯特空间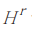 也是虚构的存在。外尔老师之所以认为正交射影的方法不太好,也许是因为正交射影的方法使用了虚构的
也是虚构的存在。外尔老师之所以认为正交射影的方法不太好,也许是因为正交射影的方法使用了虚构的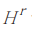 ,而这并不属于“安全”领域的范畴之内。《黎曼曲面的概念》中基于狄利克雷原理的调和函数存在证明很好地组成分段光滑函数列
,而这并不属于“安全”领域的范畴之内。《黎曼曲面的概念》中基于狄利克雷原理的调和函数存在证明很好地组成分段光滑函数列
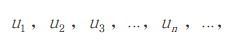
得出求其极限的调和函数
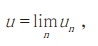
他认为该方法远比正交射影的方法“安全”。
哥德尔证明了不完全性定理,不过他的想法好像与外尔不同。
哥德尔在其论文“罗素的数理逻辑学”中指出,“集合(class)和概念(concept)是两个完全独立的实在,它与我们所说的定理或构成不同。假定类似的实在与物理学假定物体的存在一样合理。想要得到满意的物理,物体是必要条件。同样,想要得到满意的数学,实在也是必要条件”。而且,他还在“何谓康托尔的连续统假设”一文中提到:“我们对集合论的对象有着某种觉察力(perception),我认为这种感觉即数学直觉比五官的感觉更值得信任。”
总而言之,哥德尔认为数学的对象是与我们独立的实在,即实在论。而且,我们具有感知这种数学实在的能力。这与外尔的想法刚好相反,因为外尔认为数学是人类创造性活动的产物。哥德尔的想法表明,集合论是实际存在的,因此连续统的浓度ℵ 也是固定的。竹内外史与哥德尔交往颇深,据竹内所说,哥德尔“认为连续统的浓度ℵ 等于ℵ²。因为如果ℵ=ℵ²,将会呈现出一个极其美丽的世界”。
我个人非常喜欢外尔的数学研究风格。我读过他的论文和著作,深有共鸣,唯有直觉主义让我难以理解。因为我实在无法赞同希尔伯特空间不“安全”的说法。我是一名缺乏哲学素养的数学家,因此也没有资格评论外尔和哥德尔的数学哲学。我只是从自己多年从事数学研究的经验中得到一些体会,既然自然界实际存在,那么数学现象的世界应该也实际存在。虽然我也发现了一些定理,但是那并不是我的发明,而是我在探索数学现象世界的途中,偶然发现了这些散落在角落的定理。

本文经授权转载自微信公众号“图灵新知”。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 