罗赫的父亲古斯塔夫·阿道夫·罗赫（Gustav Adolf Roch），是一名皇家厨房助理，母亲是奥古斯特·卡罗琳·比特纳（Auguste Caroline Büttner）。罗赫中学时期在诺伊施塔特学校接受教育，这个时期数学还不是其主要兴趣。1857年，受父亲鼓励，罗赫进入德累斯顿理工学院学习了2年实用化学，以更好地谋求职业发展。 

在德累斯顿理工学院求学期间，罗赫遇到了人生中第1位贵人奥斯卡·夏弗·施勒米希（Oscar Xaver Schlömilch，1823-1901），他为罗赫打开了数学世界的大门。施勒米希是一位优秀的数学家，在授课中发现罗赫极有数学天赋，希望罗赫能够转学数学。罗赫也发现了自己的数学天赋，但数学专业与当时正在学习的化学专业有很大不同，再加上未曾在数学方面进行过深入系统的学习，罗赫陷入了困惑之中。施勒米希坚持不懈地劝说，终于说服了罗赫。罗赫改变了正在研究的主要课题，投身到数学理论的研究中。 

罗赫有很高的天赋，在德累斯顿理工学院学习期间，他首次接触电磁学的数学理论，就通过研读安德烈-玛丽·安培（André-Marie Ampère，1775-1836年）在1826年出版的著作《仅由经验导出的电动力学现象理论》，撰写了第1篇关于电动力学和电磁学的数学理论的论文《论安培公式的转化》，并于1859年发表在《数学和物理杂志》上。 

不久之后，还是在1859年，罗赫又发表了2篇论文《论磁矩》和《论磁学》。《论磁矩》计算了一个电流绕与坐标轴平行的3个轴旋转到另一个电流的力矩，得到了结论——韦伯关于闭合电流的实验对安培公式的证明不完全正确，加深了对安培公式的理解。《论磁学》分析了磁平衡方程的作用，促进了电磁场与电场强度的研究。这2篇文章的发表进一步展示了罗赫的天赋，促使他在这个领域不断深耕下去。

 1859年春，20岁的罗赫进入莱比锡大学，继续进行电磁学数学理论的研究。对他影响最深的老师是奥古斯特·费迪南德·默比乌斯（August Ferdinand Möbius，1790-1868年），默比乌斯在解析几何方面有独特深刻的见解。罗赫听了默比乌斯的许多讲座，这为他在数学上的深入研究提供了丰富的理论知识。罗赫好奇心强，对很多方面都富有热情，学习了许多课程，选修了哲学、植物学、语言学和历史学的一些课程，此外还聆听了威廉·汉克尔（Wilhelm Hankel）的物理讲座，学习了数学与物理之间的联系与应用，这为他研究电动力学和电磁学、位势函数等打开了新的大门。 

这段时间，罗赫继续对电磁学的数学理论深入学习，研读相关论文，并且很快有了高质量的成果。罗赫刻苦学习、勤奋钻研，尤其擅长数学、物理学科，再加上发表多篇论文，他获得了卡尔·弗里德里希·克雷格尔·冯·斯特恩巴赫（Karl Friedrich Kregel von Sternbach，1717—1789年）捐赠的奖学金——克雷格尔-斯特恩巴赫奖学金（主要用来鼓励数学、物理、天文等领域的研究）。这项奖学金为罗赫进一步研究数学和物理学提供了支持。 

1861年4月13日，在汉克尔的建议下，22岁的罗赫进入哥廷根大学，跟随威廉·爱德华·韦伯（Wilhelm Eduard Weber，1804-1891年）学习了3个学期，同时也聆听了许多顶尖数学家的讲座，其中黎曼对罗赫的影响格外深刻，黎曼以其丰富的学识、敏锐的头脑和有趣的讲座给他留下了深刻的印象，使得罗赫决定追随黎曼的脚步。与黎曼一样，罗赫同时从事位势理论和复变函数论的研究。除此之外，韦伯既是黎曼的老师，又是罗赫的老师，所以罗赫和黎曼的联系较多。在黎曼的影响下，罗赫亦对哲学产生了浓厚兴趣。 

1862年，在结束了哥廷根大学的学习后，罗赫又去了柏林。他在柏林大学生活了1个学期，学习更广泛的知识。罗赫学习了克罗内克在数论、方程理论、行列式理论和积分理论等方面的思想，使其更容易寻找多种理论之间的联系。罗赫运用库默尔将整数的结论推广到其他整环的方法，把第1类积分的结论推广到第2类积分与第3类积分上。罗赫还学习了魏尔斯特拉斯通过幂级数构建复函数理论的思想，特别是在1864年的论文运用了魏尔斯特拉斯的思想，解决单变量函数的相关问题。这段时间，罗赫的分析思想还有一个主要来源，那就是博尔夏特，博尔夏特帮助其更好地构建了复变函数框架。 

罗赫始终保持求真务实、乐于合作的品质，与鲁道夫·克莱布什（Rudolf Clebsch，1833-1872年）有一段交流。克莱布什原来的研究方向是变分法，一开始对纯数学不太了解，在得知黎曼的复变函数论工作及罗赫对这方面有研究后，向罗赫写信请教黎曼研究内容与罗赫学位论文的相关问题。罗赫热情地与克莱布什探讨这些问题并解答了他的疑惑。克莱布什吸收、借鉴黎曼和罗赫的思想，结合自己的想法给出了超越法，他是首次运用曲线术语阐述第1类阿贝尔积分定理的人。 

3.1 位势理论 

1862年，23岁的罗赫从莱比锡大学毕业，获得硕士学位，并在汉克尔指导下完成博士学位论文《论三元函数的位势表达式》，被授予博士学位。此后，他在1863年和1864年发表多篇关于位势理论的论文。 

1863年，他在《克雷尔杂志》上发表论文《位势表达式在远程分子物理的效应理论和导体上电荷运动理论中的应用》。这篇论文补充了格林定理在空间上位势函数理论中的应用，根据欧姆定律的电磁效应，解决了远距离点的电磁效应这一问题，同时还为导体中的电荷运动建立了一个方程组，并解释了该方程组的物理意义与数学意义。 

1864年，罗赫在《克雷尔杂志》上又发表了一篇关于位势理论的论文，题目为《论位势的变换》。这篇论文通过傅里叶二重积分定义单变量函数，将定义推广到多变量函数，运用极坐标变换得到位势变换的结论，使得傅里叶积分也适用于有间断点的函数，解除了函数连续性这一条件的限制。这篇论文亦是罗赫公开发表关于位势理论的最后一篇文章。

与此同时，罗赫也在研究其他数学问题。1863年，罗赫在《数学和物理杂志》上发表论文《论复变函数》。这篇论文解决了积分基本定理的均值问题，是罗赫研究代数函数论、代数几何的基础。 

3.2 黎曼-罗赫定理 

罗赫始终保持对真理的好奇心，具有不畏挫折、大胆假设、理性思考等精神品质。在狄利克雷原理当时还存在分歧的情况下，罗赫大胆地在论文中运用这个原理，给出了其最重要成果之一，即黎曼-罗赫定理。 

1864年，罗赫对黎曼的论文很感兴趣，尤其是反复研读黎曼1857年的论文《阿贝尔函数理论》。该论文提出了很多开创性想法，例如黎曼-罗赫定理中的单边不等式、雅可比反演问题、代数曲线的双有理几何和黎曼面模数的概念。罗赫对该论文中的黎曼-罗赫定理的单边不等式很感兴趣，1864年写出了论文《论代数函数中任意常数的数量》。该论文从代数函数出发，参照黎曼论文《阿贝尔函数理论》第5节和第20节等内容，运用魏尔斯特拉斯给出的超椭圆积分方法，研究常数数量的关系。在黎曼不等式的基础上，将不等式左侧和右侧的差值解析为全纯积分的某个空间的维数，给出了黎曼-罗赫定理。1865年，罗赫将这篇论文发表在《克雷尔杂志》，成为罗赫影响最深远的成果之一。 

黎曼-罗赫定理在代数曲线、代数曲面、高维簇和层上同调等方面的研究中都发挥着极其重要的作用，是研究代数几何的基础。此后，众多数学家对其进行证明和发展，如戴德金和韦伯、小平邦彦、彼得・希策布鲁赫等，杨振宁先生和罗伯特・劳伦斯・米尔斯共同提出的杨-米尔斯理论，该理论是格罗滕迪克-黎曼-罗赫定理的推广，使数学与物理关系达到新高度。 

3.3 积分问题

罗赫具有持之以恒、开拓创新的品质。1865年，他在关于复变函数论文基础上，又发表同名论文《论复变函数》，该论文解决了函数的第1类积分问题。同年还发表论文展示运用雅可比公式得到第2类和第3类椭圆积分表达式的思想，为研究椭圆积分提供了一种新方法。 

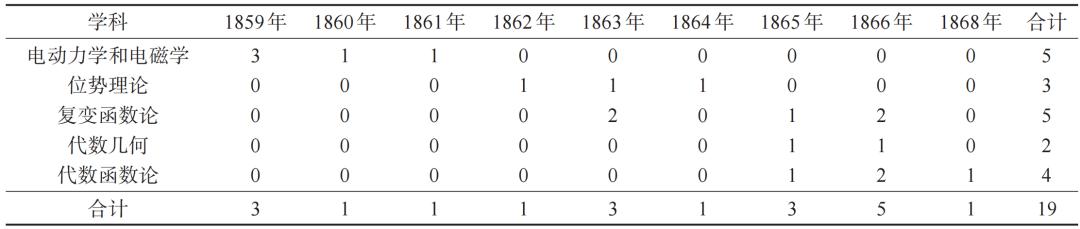
1866年，他在《数学和物理杂志》上发表多篇论文，如《论第2类积分和θ函数的均值》为研究积分中值定理提供便利；《论特殊的四重周期函数》研究超椭圆积分构造。他在《克雷尔杂志》发表的论文也推动了相关领域研究。罗赫去世后，《克雷尔杂志》于1868年发表了他的论文《论第3类阿贝尔积分》（Ueber Abelsche Integrale dritter Gattung）。该论文总结了罗赫关于第3类阿贝尔积分的研究，为罗赫系统研究阿贝尔积分画上了一个句号。根据学科的不同，将罗赫1859-1868年出版的论著进行分类、整理，如表1所示。罗赫的论文主要集中在多个领域，1859年发表首篇论文后，持续创作，1865年发表了他最著名的论文《论代数函数中任意常数的数量》。 

表1 罗赫出版论著（1859-1868年）

罗赫热爱数学、把数学当成一份事业，并为之努力奋斗。1863年，也就是获得博士学位后一年，罗赫进入哈雷大学任无薪讲师。他努力提高自己的学识，聆听多领域讲座，罗赫认为在哈雷大学任职是一种神圣使命，并在之后的岁月中努力践行。

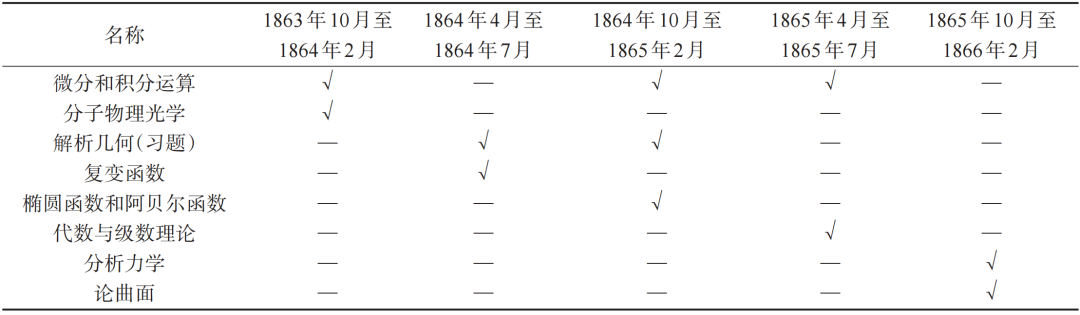
在1863-1864年、1864-1865年和1865-1866年的3个学年里，罗赫一直勤勤恳恳，反复钻研黎曼的思想，为呈现出效果更好的讲座效果，他不断学习数学和物理学知识。他在哈雷大学开设多门课程，深受学生欢迎，使学生们在数学、物理方面积累了学识，朱利叶斯・魏因加滕受他影响较大。1866年，卡尔・戈特弗里德・诺依曼整理罗赫笔记，发表两篇论文。表2是哈雷大学留存的罗赫讲座（1863-1866年）信息。 

表2 罗赫的讲座信息（1863-1866年）

1863-1866年，罗赫一直担任哈雷大学的无薪讲师。在此期间他出色的个人能力表现得淋漓尽致，得到了海因里希·爱德华·海涅的关注。1866年8月，罗赫被正式任命为哈雷大学编外教授。然而，不幸却悄然靠近。由于身患肺结核病，罗赫的身体每况愈下，获准在1866-1867年冬季学期休假，以便恢复健康。罗赫去了威尼斯，希望那里温暖的天气使身体康复。然而并没有如愿以偿，1866年11月21日，罗赫在威尼斯因肺结核逝世。然而，罗赫的名字却因黎曼-罗赫定理而永垂不朽。 

罗赫将大部分精力投身至数学和物理学科研和教学事业中，怀着对科学的热爱砥砺前行，并发表多篇论文，其论文通常篇幅不长，但其蕴含的思想丰富。特别是给出了黎曼-罗赫定理，该定理推动了代数几何的发展，为后续数学家提供了宝贵财富。他提供了研究阿贝尔积分理论的方法，促进了电动力学和电磁学、位势理论、复变函数论、代数几何、代数函数论等领域的发展。罗赫在教学上精心准备，引导学生进入知识的殿堂，吸引了更多的人投入数学事业中。罗赫虽英年早逝，但他在数学的发展史上，留下了浓浓的一笔，短暂的一生彰显了无穷的智慧。他身上具有的谦虚好学、求真务实、勇于探索、持之以恒、认真负责等精神品质，值得学习和借鉴。