1

致敬“黑匣子”发明人大卫·沃伦。他为空难黑箱找到了钥匙。

撰文 | 瞿立建

2022年3月21日下午2时许，中国东方航空5735号班机（简称东航MU5735）坠毁在广西梧州。这一天也是“黑匣子”发明者大卫·沃伦（David Warren，1925-2010）97岁诞辰的第二天。事件令所有人震惊和难过。事故原因要等分析出 “黑匣子”数据才能确定，目前，两部“黑匣子”已经找到。期待早日查明真相，告慰遇难者在天之灵，给逝者家属以交待。
 

撰文 | 王子熹

来源 | 本文首发于果壳童学馆（guokr_kid），经授权转载

喷嚏先打为敬｜猫和老鼠秋季花粉又开始飘扬了，一年一次从不缺席。花粉过敏患者已经习惯与眼睛痒、流鼻涕、打喷嚏、鼻子堵为伴，一包抽纸2天就能用完。严重的患者还会出现哮喘以及全身的皮疹，极其影响生活质量。

桑科葎草属花粉与藜科、菊科蒿属是北方夏秋季气传致敏花粉三大主要来源。过敏到底是怎么回事，和感冒有什么区别，过敏性鼻炎如何治疗？...

近日，我国南方部分地区出现特有的“回南天”现象，众网友纷纷表示“感觉像住了水帘洞”，“感觉家里的墙壁在流泪”。造成这一现象的原因是因为室外温度高，室内温度低，室内水蒸气冷凝产生的水雾布满了墙壁、地板表面，与冬季眼镜起雾道理相同。对于普通大众来说，只需等待天气继续变暖，“回南天”自然会过去。但是，对医务工作者和一些特种作业操作者来说，避免设备表面起雾则十分关键。表面防雾，这里边的门道可深了；而亲水的...

图像查看和分析软件napari填补了Python编程语言科学生态系统里的空缺。

撰文 | Jeffrey M. Perkel

翻译 | 施普林格·自然上海办公室

Josh Dorrington在观测急流（jet stream）上已经相当娴熟了。他绘制出不同高空海拔下快速移动的气流，然后将气流图一个挨一个的摆放。“你学会善于观察这所有的横切面，解开背后的含义。”Dorrington说，他是英国牛津大学的大气物理学家。不过与计算机可视化相比，这种“手动”方法比较慢，并...

吴大猷，物理学家、教育家。研究成果遍及理论物理的许多领域，撰写了专著《多原子分子结构及其振动光谱》、《量子散射理论》、《气体与等离子体的动力学方程》以及一套理论物理教程。指导帮助了一批学生发展自己的科学才能，使他们在科学上取得了突出的成就，为中国物理学的发展做出了重大贡献。

——《中国科学技术专家传略·理学编》

整理 | 遇见

美编 | 农民 

发蒙启蔽，稍通解耳

吴大猷，1907年9月29日出生于广...

在一个接一个的“小时代”里，超导研究蓬勃发展，特别是中国科学家取得了令世人瞩目的成就。要跟上时代的浪潮，了解超导的相关知识，回溯“小时代”里的历史源流，读一本图文并茂、叙事轻松的科普书适逢其时——《超导“小时代”：超导的前世、今生和未来》。如果你是吃瓜群众，可以读到科学八卦；如果你是专业学者，可以品鉴科学前沿；各有收获，找到“小时代”里的大舞台。

撰文丨姬扬

超导就是超导电性，指的是一些材料在...

一个环境变得保守僵化，失去活力，失去孩子们游戏般的快乐和创造力，失去对于科学问题本身的兴趣，怕是从这些勋宗们开始的。

撰文 | 卡洛

夜里睡不着，计划着明天吃辣子鸡，又怕和前回吃过的那一碟做得不一样，愈加睡不着了。坐起来点灯看邮件，不幸就看见了 PRL 编辑发过来的 acceptance letter，

Dear xxx, we are pleased to inform you that your manuscript has been accepted for publication ……

没办法，工作没日没夜...

撰文 | 鞠强（粒子、弦与宇宙学硕士）

星星为什么会发光？太阳为什么会发光？

而今，在面向小朋友的天文科普书里也可以看到对恒星发光机制的解释。但在100年前，这个研究领域是片空白。

图丨wiki

对于“恒星发光”的问题，人类一直充满好奇和探究。比如，关于“太阳发光的原因”，古希腊哲学家阿那克萨戈拉认为太阳是一块炽热的石头，后来英国天文学家威廉·赫歇尔在1800年发现了太阳的红外辐射，还提出太阳发光是因为它有炽...

1882年3月24日，德国微生物学家科赫（Robert Koch）宣布发现了结核病的病原体：结核分枝杆菌。1921年6月，法国细菌学家卡尔梅特（Albert Calmette）与其助手介兰（Camille Guérin）培养牛分枝杆菌而研发的结核疫苗第一次应用于人体，这便是以两人名字命名的“卡介苗”（Bacille Calmette-Guérin vaccine，简称BCG）。

如今，卡介苗问世已过百年，仍是目前唯一被批准用来抗击结核病的疫苗。但结核这个恶魔却从来没有被彻底打败...

撰文 | 丁崝

住着价值数百亿的“豪宅”，却没法点个外卖。明明是一天能看16次日出的阳光“宙景房”，但连窗户都不能开……

在距地面400km 高度的中国空间站上，航天员们的日常生活跟地球上相比，有很多不同的地方，而关于航天员的生活，也流传着很多有趣的说法，其中有些多少与事实沾边，有些则是彻头彻尾的瞎编，今天咱们就来梳理一下，看看关于航天员日常生活的说法，到底靠不靠谱。

由于空间站是密闭环境，且补充给...

Dennis Parnell Sullivan
 

挪威科学与文学院决定将 2022 年阿贝尔奖授予美国纽约市立大学研究生院及大学中心以及美国纽约州立大学石溪分校的丹尼斯·帕内尔·苏利文 (Dennis Parnell Sullivan)，“以表彰其在最广泛意义上对拓扑学的开创性贡献，尤其是代数、几何及动力学方面”
 

获奖者简介

苏利文，图片来自阿贝尔奖官网

丹尼斯·帕内尔·苏利文是一名美国数学家，其最著名的成就是在拓扑学及动力系统方面的开拓性研究...

物理学家P.W.安德森（Philip Anderson）因无序和磁性材料方面的工作获得1977年诺贝尔物理学奖，但这并不足以彰显他的贡献。他推动多体理论与固体物理的融合，最终形成了如今的凝聚态物理，堪称凝聚态物理的宗师。在经典论文“more is different”中，安德森驳斥了物理学界长期弥漫的还原论观点，认为自然在不同尺度上会涌现出新的复杂性。在这之后，更是参与创建了复杂系统研究的圣地——圣塔菲研究所。安德森于2020年3月29日逝世...

撰文 | Innorld

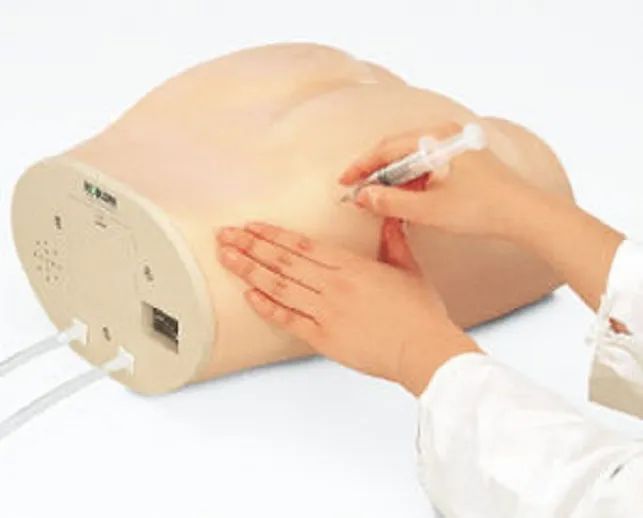
曾经“风靡”的屁股针
 

所谓“屁股针”是指臀部肌肉注射。
 

曾经，这种给药方式非常常见，尤其是儿童，几乎没有人没有挨过屁股针的扎，没有“享受”屁股针的疼痛。

这主要是因为，感染性疾病是威胁人类健康的最常见疾病，尤其是婴幼儿和儿童。

在古代，人类平均预期寿命之所以长期徘徊在30到35岁的水平，最根本的原因就是传染和感染性疾病导致的婴幼儿和儿童的大量死亡。

尽管，工业革命后这种状况有了一定...

上周，西湖大学宣布将于今年招收第一批本科生；3月19日，西湖大学校长施一公教授在网络上进行了招生宣讲直播，并回应了 “生化环材是四大天坑专业”的说法。不过，网友们的关于“天坑专业”的争论仍然没有止息。有感于此，毕业于清华大学颜宁实验室的博士、现任人大附中高级教师的和渊老师提出了自己的看法。

撰文 | 和渊（中国人民大学附属中学高级教师）

“21世纪是生命科学的世纪”，这句话已经流传了许多年，但同时也有...

2022年3月15日，尤金·帕克逝世，享年94岁。帕克天纵英才，30岁时就严格证明太阳风的存在，并因此声名大噪。在60年的学术生涯中，他以唯一作者的身份发表了200多篇研究论文，重塑了人类对太阳物理、等离子体物理、各种尺度上的磁场的性质的认识。现在，以他的姓命名的价值15亿美元的“帕克太阳探测器”正继承他的遗志，破解太阳的秘密。尽管帕克不再与我们同在，但他的发现与学术遗产会永远伴随着人类。

撰文 | 王善钦

芝加...

撰文 | 叶译楚

新一轮疫情快速席卷全国20多个省，新增确诊病例不断出现。截至3月17日12时，全国31个省（自治区、直辖市）和新疆生产建设兵团报告现有确诊病例12326例。

3月15日晚，国家卫健委及国家中医药管理局发布了《新型冠状病毒肺炎诊疗方案（试行第九版）》（以下简称《方案》）。

在最新版《方案》中，推荐了两款“新冠特效药”——安巴韦单抗/罗米司韦单抗注射液和奈玛特韦片/利托那韦片组合包装（Paxlovid）[...

为什么我们长得左右差不多对称，身体里的器官却不对称？

撰文 | Catherine Offord

编译 | 继省

蓦然回“手”——意外进入细胞手性研究领域

时钟拨回到2009年的一天。科学家万群（Leo Wan）正在用显微镜观察他培养的小鼠细胞。看着看着，他发现这些小鼠细胞不太对劲儿，像是长“拧劲儿”了。这批细胞的名字是成肌肉细胞（myoblast），顾名思义可以生成肌肉，是肌肉细胞的前身。他所培养的数百个成肌肉细胞长在了一个微...

编辑人语：物理学的大厦由一块一块的砖头有机地构建起来，物理学的概念就是砖头。学习物理学首先要深刻理解概念，建立物理图像。赵凯华先生2011年1月发表于《物理教学》的这篇文章，通过辨析重力和重量等名称，强调重力这个概念是精确的、普适的，尽管在地球上不同地方同一个物体经受的重力有所不同。在物理的教学中，特别是中学物理的教学中，常常有把活生生的物理变成名词解释的做法，必须摒弃这一做法。经赵先生同意，本期微信号...

返朴作者按：

“博学而笃志，切问而近思。”语出《论语·子张》。按照“百度百科”的解释，其意思就是“博览群书广泛学习，而且能坚守自己的志向，恳切地提问，多考虑当前的事。”虽然这是一条我在复旦中学附小、复旦中学和复旦大学求学以及工作到退休的母校的共同校训，但是长期以来一直是“小和尚念经——有口无心”，甚至不太明白这条校训确切说的是什么意思。退休以后在从事脑科学科普工作时，为了弄明白现有的脑科学知识是怎...

1943年，冯·卡门创办“Quarterly of Applied Mathematics”(《应用数学季刊》)，并执笔完成“Tooling up mathematics for engineering”(《用数学武装工程科学》)一文刊登于创刊号卷首。文章通过数学家与工程师对话的形式，阐释数学与应用科学间的关系。其中的很多观点，今天看来仍颇富启示作用。

撰文 | 冯·卡门

翻译 | 李家春、戴世强

人们常说，研究数学的主要目的之一是为物理学家和工程师们提供解决实际问题的工具。从数...